Comparison of electoral systems

Electoral systems are the rules for conducting elections. Comparisons between different systems can focus on different aspects: on suffrage or rules for voter eligibility; on candidate eligibility and the rules governing political parties; on the way elections are scheduled, sequenced, and combined; or on the rules for determining the winner within a given election (also called the "election rule" or "voting method").

Part of the Politics series
Electoral Systems
Plurality/majoritarian
  • Multi-round voting
Proportional representation
Mixed systems
Other systems and related theory
 Politics portal

With electoral systems one can also focus on the internal voting mechanism that reviews, for instance, in how far the voters' choices are reflected in the outcome. The mechanism can help show that candidates need to focus differently to improve their odds of winning a seat.

According to a 2006 survey of electoral system experts, their preferred voting methods were, in order of preference:[1]

  1. Mixed member proportional
  2. Single transferable vote
  3. Open list proportional
  4. Alternative vote (Instant Runoff aka Ranked Choice)
  5. Closed list proportional
  6. Single member plurality
  7. Runoffs
  8. Mixed member majoritarian
  9. Single non-transferable vote

Direct comparisons between first-past-the-post and proportional voting

Though there are many different systems, including a large number of combinations of systems, there are two extremes in the range of voting systems that are very different from one another. Viewing the differences between these two can help to attain a quick overview about some of the differences between electoral systems and why the differences have significant political implications. The two systems are:

First-past-the-post voting: A single candidate wins the seat of a single district, county or nation, by getting the most votes in a geographical area. Here, "most" means more votes than any other candidate, which can be less than 50 percent of the votes, for example, 20 or 30 percent of the votes. This can be termed a "relative majority" or a "plurality".

Proportional voting: The entire outcome of votes in a municipality or nation translates collectively into the outcome of the seats.

  • Where a geographical connection is automatically incorporated in the electoral outcomes in nations with first-past-the-post (or winner-take-all), there is no certainty about geographical representation in proportional voting. It may play a role with the selection of the candidates, but when geographically inclined voters need to be alert whether candidates are from their own region or area and vote appropriately.
  • In first-past-the-post, voters are represented by a single representative, whether they voted for the candidate or someone else. With proportional voting, virtually every voter can point to the representative they voted for.
  • If decisions in the elected body are also made by a relative majority of the elected representatives, then the relative majority of the decision-making votes combines with the fact that the representatives won their seats with only a relative majority of their constituents' votes. In effect, this strong dual mechanism diminishes the constituents' importance in the decision; if a seat is obtained with 20 percent of the vote (which can occur), and a decision is subsequently made with 40 percent of the council members, then the voters' input can be declared as diminished, since about 12 percent of voters have indirectly made the winning decision. If decisions made in proportional voting are won with an absolute majority of the votes by the people who got their seats based on the direct distribution of the constituents' votes, then there is at worst a 50 percent weakening in the representation of voters' opinions, in the sense that a decision represents (indirectly, via the representatives) at least 50 percent of the voters.
  • Regions with a first-past-the-post system tend to have a stabilizing factor built in because third-party candidates will have a harder time beating out candidates from Party One and Party Two. Cabinets will not often be based on coalitions and will therefore tend to stay in power for a long time. In general, the two major parties will have no problem absorbing third-party issues as their own, covering any gaps both forgot to cover collectively. Both parties may therefore deliver close to what the voters want. Contrast this with the absence of built-in stability of proportional voting, in which two, sometimes three parties or more, need to cooperate to obtain a workable majority. This shows how one system is more accustomed to having a more vertical power structure whereas the other is more collaborative or horizontal in nature.
  • Regions with first-past-the-post have a focus on the center of the constituency. To win a seat, a candidate X must appeal to as many voters as possible, and try to split the remaining votes among rival candidates, so that all the other candidates receive lower support than X. In proportional voting, the focus can follow a party-based policy, and the political message can be quite honest and direct. It is possible that a party obtains seats appealing to voters on the single issue, for example, of non-human animal rights. Candidates and representatives handle information differently in the two extreme systems because the arithmetic of winning seats differs between the two systems.

Methodologies for comparison of voting methods

Attitudes towards systems are highly influenced by the systems' impact on groups that one supports or opposes, which can make the objective comparison of electoral systems difficult. There are three notable methodologies commonly used for the comparison of electoral systems:

  1. Criteria can be defined mathematically, such that any voting method either passes or fails. This gives perfectly objective results, but their practical relevance is debatable.
  2. Define ideal criteria that no voting method passes perfectly, and then see how often or how close to passing various methods are over a large sample of simulated elections. This gives results which are practically relevant, but the parameters of the simulation can still be biased.
  3. Create imprecisely defined criteria, and then assign a neutral body to evaluate each method according to these criteria. This approach can look at aspects of voting methods which the other two approaches miss, but both the definitions of these criteria and the evaluations of the methods are still inevitably subjective.

Mathematical criteria

Historically, voting theorists have relied heavily on the first methodology, the use of voting method criteria which define potentially desirable properties of voting methods mathematically for comparing voting methods fairly and independently of political ideologies.

While the passing or failing of a given criterion is mathematically provable, using them to compare methods does not make the comparison completely objective. For example, it is relatively easy to devise a criterion that is met by one's preferred voting method, and by very few other methods. Doing this, one can then construct a biased argument for the criterion, instead of arguing directly for the method. There is no ultimate authority on which criteria should be considered more important than others. This is further complicated by the fact that no voting method can pass all the desirable criteria, and that there are many of them.

The following criteria, which apply to single-winner voting methods, are considered to be desirable by many voting theorists:

Result criteria (absolute)

These are criteria that state that, if the set of ballots is a certain way, a certain candidate must or must not win.

Majority criterion (MC)
Will a candidate always win who is ranked as the unique favorite by a majority of voters? This criterion comes in two versions:
  1. Ranked majority criterion, in which an option which is merely preferred over the others by a majority must win. (Passing the ranked MC is denoted by "yes" in the table below, because it implies also passing the following:)
  2. Rated majority criterion, in which only an option which is uniquely given a perfect rating by a majority must win. The ranked and rated MC are synonymous for ranked voting methods, but not for rated or graded ones. The ranked MC, but not the rated MC, is incompatible with the IIA criterion explained below.
Mutual majority criterion (MMC)
Will a candidate always win who is among a group of candidates ranked above all others by a majority of voters? This also implies the majority loser criterion – if a majority of voters prefers every other candidate over a given candidate, then does that candidate not win? Therefore, of the methods listed, all pass neither or both criteria, except for Borda, which passes Majority Loser while failing Mutual Majority.
Condorcet criterion
Will a candidate always win who beats every other candidate in pairwise comparisons? (This implies the majority criterion, above.)
Condorcet loser criterion (cond. loser)
Will a candidate never win who loses to every other candidate in pairwise comparisons?

Result criteria (relative)

These are criteria that state that, if a certain candidate wins in one circumstance, the same candidate must (or must not) win in a related circumstance.

Independence of Smith-dominated alternatives (ISDA)
Does the outcome never change if a Smith-dominated candidate is added or removed (assuming votes regarding the other candidates are unchanged)? Candidate C is Smith-dominated if there is some other candidate A such that C is beaten by A and every candidate B that is not beaten by A etc. Note that although this criterion is classed here as nominee-relative, it has a strong absolute component in excluding Smith-dominated candidates from winning. In fact, it implies all of the absolute criteria above.
Independence of irrelevant alternatives (IIA)
Does the outcome never change if a non-winning candidate is added or removed (assuming voter preferences regarding the other candidates are unchanged)?[2] For instance, plurality rule fails IIA; adding a candidate X can cause the winner to change from W to Y even though Y receives no more votes than before.
Local independence of irrelevant alternatives (LIIA)
Does the outcome never change if the alternative that would finish last is removed? (And could the alternative that finishes second fail to become the winner if the winner were removed?)
Independence of clone alternatives (cloneproof)
Does the outcome never change if non-winning candidates similar to an existing candidate are added? There are three different phenomena which could cause a method to fail this criterion:
Spoilers
Candidates which decrease the chance of any of the similar or clone candidates winning, also known as a spoiler effect.
Teams
Sets of similar candidates whose mere presence helps the chances of any of them winning.
Crowds
Additional candidates who affect the outcome of an election without either helping or harming the chances of their factional group, but instead affecting another group.
Monotonicity criterion (monotone)
If candidate W wins for one set of ballots, will W still always win if those ballots change to rank W higher? (This also implies that you cannot cause a losing candidate to win by ranking them lower.)
Consistency criterion (CC)
If candidate W wins for one set of ballots, will W still always win if those ballots change by adding another set of ballots where W also wins?
Participation criterion (PC)
Is voting honestly always better than not voting at all? (This is grouped with the distinct but similar Consistency Criterion in the table below.[3])
Reversal symmetry (reversal)
If individual preferences of each voter are inverted, does the original winner never win?

Ballot-counting criteria

These are criteria which relate to the process of counting votes and determining a winner.

Polynomial time (polytime)
Can the winner be calculated in a runtime that is polynomial in the number of candidates and linear in the number of voters?
Resolvable
Can the winner be calculated in almost all cases, without using any random processes such as flipping coins? That is, are exact ties, in which the winner could be one of two or more candidates, vanishingly rare in large elections?
Summability (summable)
Can the winner be calculated by tallying ballots at each polling station separately and simply adding up the individual tallies? The amount of information necessary for such tallies is expressed as an order function of the number of candidates N. Slower-growing functions such as O(N) or O(N2) make for easier counting, while faster-growing functions such as O(N!) might make it harder to catch fraud by election administrators.

Strategy criteria

These are criteria that relate to a voter's incentive to use certain forms of strategy. They could also be considered as relative result criteria; however, unlike the criteria in that section, these criteria are directly relevant to voters; the fact that a method passes these criteria can simplify the process of figuring out one's optimal strategic vote.

Later-no-harm criterion, and later-no-help criterion
Can voters be sure that adding a later preference to a ballot will not harm or help any candidate already listed?[4]
No favorite betrayal (NFB)
Can voters be sure that they do not need to rank any other candidate above their favorite in order to obtain a result they prefer?[5]

Ballot format

These are issues relating to the expressivity or information content of a valid ballot.

Ballot type
What information is the voter given on the ballot?
Equal ranks
Can a valid ballot express equal support for more than one candidate (and not just equal opposition to more than one)?
Over 2 ranks
Can a ballot express more than two levels of support/opposition for different candidates?

Weakness

Note on terminology: A criterion is said to be "weaker" than another when it is passed by more voting methods. Frequently, this means that the conditions for the criterion to apply are stronger. For instance, the majority criterion (MC) is weaker than the multiple majority criterion (MMC), because it requires that a single candidate, rather than a group of any size, should win. That is, any method which passes the MMC also passes the MC, but not vice versa; while any required winner under the MC must win under the MMC, but not vice versa.

Compliance of selected single-winner methods

The following table shows which of the above criteria are met by several single-winner methods.

Sort:
Criterion



Method
 Maj­ority Maj.
loser		 Mutual
maj.		 Cond­orcet Cond.
loser		 Smith/
ISDA		 LIIA IIA Clone­proof Mono­tone Consis­tency Partic­ipation Rever­sal
sym­metry		 Poly­time/
resolv­able		 Summ­able Later-no- No
favorite
betrayal		 Ballot
type		 Ranks
Harm Help = >2
Appr­oval Rated[lower-alpha 1] No No No[lower-alpha 2][lower-alpha 3] No No[lower-alpha 2] Yes Yes[lower-alpha 4] Yes[lower-alpha 5] Yes Yes Yes Yes O(N) Yes O(N) No Yes[lower-alpha 6] Yes Approvals Yes No
Borda count No Yes No No[lower-alpha 2] Yes No No No Teams Yes Yes Yes Yes O(N) Yes O(N) No Yes No Ranking No Yes
Bucklin Yes Yes Yes No No No No No No Yes No No No O(N) Yes O(N) No Yes If equal preferences Ranking Yes Yes
Cope­land Yes Yes Yes Yes Yes Yes No No[lower-alpha 2] Teams,
crowds		 Yes No[lower-alpha 2] No[lower-alpha 2] Yes O(N2) No O(N2) No[lower-alpha 2] No No[lower-alpha 2] Ranking Yes Yes
IRV (AV) Yes Yes Yes No[lower-alpha 2] Yes No[lower-alpha 2] No No Yes No No No No O(N2) Yes[lower-alpha 7] O(N!)[lower-alpha 8] Yes Yes No Ranking No Yes
Kemeny–Young Yes Yes Yes Yes Yes Yes Yes No[lower-alpha 2] Spoil­ers Yes No[lower-alpha 2]
[lower-alpha 9]		 No[lower-alpha 2] Yes O(N!) Yes O(N2)[lower-alpha 10] No[lower-alpha 2] No No[lower-alpha 2] Ranking Yes Yes
Highest median/Majority
judgment[lower-alpha 11]		 Rated[lower-alpha 12] Yes[lower-alpha 13] No[lower-alpha 14] No[lower-alpha 2][lower-alpha 3] No No[lower-alpha 2] Yes Yes[lower-alpha 4] Yes Yes No[lower-alpha 15] No[lower-alpha 16] Dep­ends[lower-alpha 17] O(N) Yes O(N)[lower-alpha 18] No[lower-alpha 19] Yes Yes Scores[lower-alpha 20] Yes Yes
Mini­max Yes No No Yes[lower-alpha 21] No No No No[lower-alpha 2] Spoil­ers Yes No[lower-alpha 2] No[lower-alpha 2] No O(N2) Yes O(N2) No[lower-alpha 2][lower-alpha 21] No No[lower-alpha 2] Ranking Yes Yes
Plura­lity/FPTP Yes No No No[lower-alpha 2] No No[lower-alpha 2] No No Spoil­ers Yes Yes Yes No O(N) Yes O(N) N/A[lower-alpha 22] N/A[lower-alpha 22] No Single mark N/A No
Score voting No No No No[lower-alpha 2][lower-alpha 3] No No[lower-alpha 2] Yes Yes[lower-alpha 4] Yes Yes Yes Yes Yes O(N) Yes O(N) No Yes Yes Scores Yes Yes
Ranked pairs Yes Yes Yes Yes Yes Yes Yes No[lower-alpha 2] Yes Yes No[lower-alpha 2] No[lower-alpha 16][lower-alpha 2] Yes O(N3) Yes O(N2) No[lower-alpha 2] No No[lower-alpha 16][lower-alpha 2] Ranking Yes Yes
Runoff voting Yes Yes No No[lower-alpha 2] Yes No[lower-alpha 2] No No Spoil­ers No No No No O(N)[lower-alpha 23] Yes O(N)[lower-alpha 23] Yes Yes[lower-alpha 24] No Single mark N/A No[lower-alpha 25]
Schulze Yes Yes Yes Yes Yes Yes No No[lower-alpha 2] Yes Yes No[lower-alpha 2] No[lower-alpha 16][lower-alpha 2] Yes O(N3) Yes O(N2) No[lower-alpha 2] No No[lower-alpha 16][lower-alpha 2] Ranking Yes Yes
STAR
voting		 No[lower-alpha 26] Yes No[lower-alpha 27] No[lower-alpha 2][lower-alpha 3] Yes No[lower-alpha 2] No No No Yes No No Depends[lower-alpha 28] O(N) Yes O(N2) No No No[lower-alpha 29] Scores Yes Yes
Sortition, arbitrary winner[lower-alpha 30] No No No No[lower-alpha 2] No No[lower-alpha 2] Yes Yes No Yes Yes Yes Yes O(1) No O(1) Yes Yes Yes None N/A N/A
Random ballot[lower-alpha 31] No No No No[lower-alpha 2] No No[lower-alpha 2] Yes Yes Yes Yes Yes Yes Yes O(N) No O(N) Yes Yes Yes Single mark N/A No

This table is not comprehensive. For example, Coombs' method, which satisfies many of the criteria, is not included.

Compliance of party-based multi-winner methods

The following table shows which of the above criteria are met by several party-based multiple winner methods.

Criterion

Method
 Proportional in theory Proportional in practice Semi-proportional

a majority of voters cannot force the result to be one such that they win all seats

 Not breakable voting method does not have a potential strategic voting feedback loop
 Monotone Consistency Participation Universally Liked Candidates Are there tiers of members? Is local representation required? Is there voter selection of individual candidates? Ballot
Type
General ticket No No No No – Two-party domination Yes Yes Yes No No No No — all seats are filled from one pre-determined list Single mark for one list
Closed party-list Yes Yes Yes Yes (unless few seats or high first seat threshold) Yes Yes Yes N/A – a universally liked list would have to win all the seats by definition No No No — the ranking of candidates within the party's list determines the order by which the party's seats are filled Single mark for one list
Relatively closed party-list Yes Yes Yes Yes (unless few seats or high first seat threshold) Yes Yes Yes N/A – a universally liked list would have to win all the seats by definition No No Yes — a candidate needs to obtain a Hare quota to be guaranteed a seat, otherwise the ranking of candidates within the party's list determines the order by which the party's seats are filled Single or limited marks for candidates within one list
More open party-list Yes Yes Yes Yes (unless few seats or high first seat threshold) Yes Yes Yes N/A – a universally liked list would have to win all the seats by definition No No Yes — a candidate needs to obtain a proportion of the votes to be guaranteed a seat, otherwise the ranking of candidates within the party's list determines the order by which the party's seats are filled Single or limited marks for candidates within one list
Most open party-list Yes Yes Yes Yes (unless few seats or high first seat threshold) Yes Yes Yes N/A – a universally liked list would have to win all the seats by definition No No Yes — the number of votes every candidate receives determines the order by which the party's seats are filled Single mark for one candidate within one list
Party-list with panachage Yes Yes Yes Yes (unless few seats or high first seat threshold) Yes Yes Yes N/A – a universally liked list would have to win all the seats by definition No No Yes — the number of votes every candidate receives determines the order by which the party's seats are filled Limited marks for candidates within all lists
Unmodified Mixed-member proportional No – strategic voters can manipulate the number of overhang seats Yes, excluding disproportionalities caused by overhang seats — proportional tier members are selected to compensate for any disproportionality caused by the constituency tier, based on the proportional tier votes only Yes No – Overhang manipulation and two-party domination among single winner seats Yes No Yes Partially — a universally liked list would have to win all the seats in both the proportional and constituency tiers by definition; if all constituency candidates are universally liked, the selection of proportional tier members would be made to compensate for the ensuing disproportionality in overall membership Yes — constituency tier and proportional tier Yes — single-member constituencies Yes — constituency candidates are selected by a single-winner method; selection of proportional tier members may be done by any of the party-list methods mentioned above Single mark or ranking for one constituency candidate; proportional tier marks depend on the exact method used for selection
Best-loser Mixed-member proportional No – strategic voters can manipulate the number of overhang seats Yes, excluding disproportionalities caused by overhang seats — proportional tier members are selected to compensate for any disproportionality caused by the constituency tier, based on the party's totals Yes No – Overhang manipulation and two-party domination among single winner seats Yes No Yes No — a universally liked list would have to win all the seats in both the proportional and constituency tiers by definition — since the proportional tier members are drawn from the constituency losers, such a feat is impossible; if all constituency candidates are universally liked, the selection of proportional tier members would be made to compensate for the ensuing disproportionality in overall membership Yes — constituency tier and proportional tier Yes — single-member constituencies Yes — constituency candidates are selected by a single-winner method; proportional tier members are selected by a party-list method Single mark or ranking for one constituency candidate; proportional tier determined by the constituency tier results
Parallel voting No No — constituency tier and proportional tier members are selected independently of each other Yes No – Two-party domination among single winner seats Yes No Yes Partially — a universally liked list would have to win all the seats in the proportional tier by definition; if all constituency candidates are universally liked, the selection of proportional tier members would be unaffected Yes — constituency tier and proportional tier Yes — single-member constituencies Yes — constituency candidates are selected by a single-winner method; proportional tier members are selected by a party-list method Single mark or ranking for one constituency candidate; proportional tier marks depend on the exact method used for selection
Scorporo No – strategic voters can split the ticket to unhinge the compensatory subtraction, thus reverting the election into Parallel voting Partially — constituency tier and proportional tier members are selected independently of each other, but the constituency winners' votes are subtracted from their respective party lists' totals Yes No – decoy lists No No No Yes — a universally liked list still has the votes of its constituency winners subtracted from its own total, thus ensuring proportional distribution between all the other seats; if all constituency candidates are universally liked, the selection of proportional tier members would be made with their votes subtracted from their parties' totals Yes — constituency tier and proportional tier Yes — single-member constituencies Yes — constituency candidates are selected by a single-winner method; proportional tier members are selected by a party-list method Single mark or ranking for one constituency candidate; proportional tier marks depend on the exact method used for selection
Majority bonus system Partially – a majority of seats are distributed proportionally between the parties, but the rest are given as a bonus to the most-voted for party; Strategic voters can manipulate this bonus Partially – a majority of seats are distributed proportionally between the parties, but the rest are given as a bonus to the most-voted for party Yes No – Two-party domination among parties competing for bonus Yes Yes Yes N/A – a universally liked list would have to win all the seats by definition Yes — proportional tier and bonus tier No Not necessarily — selection of proportional tier members may be done by any of the party-list methods mentioned above Proportional tier marks depend on the exact method used for selection; bonus tier determined by the proportional tier results
Majority jackpot system No — the jackpot is assigned to the most-voted-for party, and the non-jackpot tier seats are distributed proportionally between all others; Strategic voters can manipulate the jackpot No — the jackpot is assigned to the most-voted-for party, and the non-jackpot tier seats are distributed proportionally between all others Yes No – Two-party domination among parties competing for jackpot No — the party gaining the jackpot gains an advantage over all others; the jackpot turns into a disadvantage for the most-voted-for party if it gained a greater share of seats than the jackpot Yes Yes N/A – a universally liked list would have to win all the seats by definition Yes — proportional tier and jackpot tier No Not necessarily — selection of proportional tier members may be done by any of the party-list methods mentioned above Proportional tier marks depend on the exact method used for selection; jackpot tier determined by the proportional tier results
Dual-member proportional No – strategic voters can theoretically manipulate the results in secondary seats Yes Yes No – Secondary seat manipulation and two-party domination among primary seats No Yes Yes Yes No Yes — dual-member constituencies Yes — the candidate with the most votes is guaranteed a seat, and the other is selected from among the best losers Single mark for one candidate or pair of candidates
Rural–urban proportional representation No – strategic voters can manipulate the number of rural overhang seats Partially — disproportionalities may be caused by use of STV in urban seats, as well as overhang rural seats — rural proportional tier members are selected to compensate for any disproportionality caused by the rural constituency tier, but no such compensation exists for urban disproportionalities Yes No – overhang manipulation and two-party domination among rural single winner seats No No No Partially — yes in the urban tier; a universally liked rural list would have to win all the seats in the rural proportional tier by definition; if all rural constituency candidates are universally liked, the selection of rural proportional tier members would be made to compensate for the disproportionality; in either case, the selection of urban candidates would be unaffected Yes — urban tier, rural constituency tier and rural proportional tier Yes — urban constituencies and single-member rural constituencies Yes — rural constituency candidates are selected by STV; rural constituency candidates are selected by a single-winner method; rural proportional tier members may be selected by a party-list method or from among the best losers in the rural constituencies Ranking for urban constituency candidates; single mark or ranking for one rural constituency candidate; rural proportional tier marks depend on the exact method used for selection

Compliance of non-majoritarian party-agnostic multi-winner methods

The following table shows which of the above criteria are met by several multiple winner methods.

This list is incomplete; you can help by adding missing items with reliable sources.
Criterion

Method
 Proportional Mono­tone Consis­tency Warren's Multi-Winner Partic­ipation Criterion No
Favorite
Betrayal		 Semi­honest Universally Liked Candidates With Single
Winner		 Ballot
Type
Monroe's (score voting version) Yes Depends on tiebreaker used Yes No No Approval or Range Approvals or scores
Chamberlin-Courant Rule
Ebert's Yes No Yes Approval or Range Approvals or scores
Psi Yes Yes Yes No No No Approval or Range Approvals or scores
Harmonic Yes Yes Yes No No No Approval or Range Approvals or scores
Sequential Proportional Approval Yes Yes No No No No Approval Approvals
Re-weighted Range Yes Yes No No No No Range Scores
Proportional Approval Yes Yes Yes No No No Approval Approvals
Bid voting Yes No No Yes Approval or Range Approvals or scores
Single Transferable Vote Yes No No No No No Yes Instant Runoff Rankings
CPO-STV Yes No No No No No Yes A Condorcet method (depends on which one) Rankings
Schulze STV Yes Yes No No No No Yes Schulze Rankings
Expanding Approvals Rule Approval Approvals
Single non-transferable vote No Yes Yes Yes No No N/A (not proportional) Plurality Single mark
Limited vote No Yes Yes Yes No[6] No N/A (not proportional) Plurality Limited marks
Cumulative voting No Yes Yes Yes No[6] No N/A (not proportional) Plurality Multiple marks
Minmax Approval Approval Approvals
Sortition, Arbitrary Winner No Yes Yes Yes Yes Yes N/A (not proportional) Sortition, arbitrary winner None
Single Random Ballot No Yes Yes Yes Yes Yes N/A (not proportional) Random Ballot Limited marks
Multiple Random Ballots Approaches Yes Yes Yes Yes Yes N/A (not proportional) Random Ballot Limited rankings

Compliance of majoritarian party-agnostic multi-winner methods

The following table shows which of the above criteria are met by several multiple winner methods.

This list is incomplete; you can help by adding missing items with reliable sources.
Criterion

Method
 Mono­tone Consis­tency Partici­pation Clone­proof No favoritebetrayal Semi­honest Smith setwinners Condorcetwinner Condorcetloser With singlewinner Ballottype
Multiple Winner Approval Yes Yes Yes Yes[lower-alpha 5] Yes Yes No No No Approval Approvals
Multiple Winner Range Yes Yes Yes Yes Yes Yes No No No Range Scores
Multiple Winner Schulze Yes No No Yes No No Yes Yes Yes Schulze Rankings
At Large Yes Yes Yes No

(spoilers)

 No No No No No Plurality Limited marks

Experimental metrics
Main articles: Social utility efficiency and Bayesian regret

With the advent of computer modeling and modern statistics, the field of voting theory has also adopted the second methodology, simulating large numbers of elections on a computer in order to predict the frequency of various scenarios and see how various voting methods compare in practical terms. Since such investigations are more difficult than simply proving that a given method does or does not satisfy a given mathematical criterion, results are not available for all methods. Also, these results are sensitive to the parameters of the model used to generate virtual elections, which can be biased either deliberately or accidentally.

This has led to a number of different metrics:

  • Single-winner metrics
    • Social Utility Efficiency (SUE) measures how favorable an election outcome is, on average, to all voters.[7] It is also known as Utilitarian Efficiency,[8] Voter Satisfaction Index (VSI),[9] Voter Satisfaction Efficiency (VSE),[10] or simply "Effectiveness".[11]
      • The name "Bayesian regret" (BR) is given to a similar utility metric that is inverted and non-normalized.[12]
      • Another similar utility metric is Mean Squared Error (MSE), a non-linear version applied to the position of the winner vs the voters on a one-dimensional political spectrum.[13]
    • Egalitarian-Utility Efficiency (EUE) measures how favorable the election outcome is to the least-satisfied voter.[14]
    • Condorcet Efficiency measures the likelihood that a voting method will elect the Condorcet winner.[7]
  • Multi-winner metrics
    • Condorcet Committee Efficiency (CCE) measures the likelihood that a group of elected winners would beat all losers in pairwise races.[15]
    • Social-Utility Proportionality (SUP) measures the likelihood that each voter has at least one high-utility candidate among the winners.[14]
    • Egalitarian-Utility Proportionality (EUP) measures proportionality in terms of the voter with the lowest utility for the closest winning candidate.[14]
    • Centrist Tendency (CT) measures the likelihood of a method to elect candidates near the center or extremes of a political spectrum.[14]

Such simulations are sensitive to their assumptions, particularly with regard to voter strategy, but by varying the assumptions they can give repeatable measures that bracket the best and worst cases for a voting method.[16] Parameters that may be varied include:[17][18]

  • Voting system
  • Number of voters and their ideological distribution
  • Number of candidates and their ideological distribution
  • How the utility of a candidate to each voter is modeled
  • How informed voters are of the expected behavior of other voters
  • Honest vs strategic voting, and types of strategy

The most realistic parameters for a simulation would vary depending on the country and political climate.

Many simulations of voting methods have been run to date, and relative conclusions found tend to be generally consistent.

Social utility / voter satisfaction

One desirable feature that can be explored in this way is the likelihood of a voting method to elect the candidate which maximizes voter utility or satisfaction, originally proposed by Laplace in 1795.[19][20]

This metric was introduced in a series of papers by Robert J. Weber, the inventor of Approval voting, in 1977, who calculated a voting system's "effectiveness" analytically for infinite voters using the impartial culture model.[11] He used this process to analyze First-past-the-post, two Approval variants, and Borda (in increasing order of effectiveness).

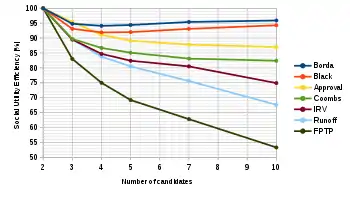
Merrill's efficiency results with an impartial culture model and 25 voters[21]

The same metric was developed further by Samuel Merrill III in the 1980s, under the name "social utility efficiency", using both a spatial model and impartial culture model, calculated statistically from random samples, with 25–201 voters and 2–10 candidates.[7] This analysis included FPTP, Runoff, IRV, Coombs, Approval, Black, and Borda (in increasing order of efficiency).

Bordley ran similar simulations in 1983, though he measured only total utility, not normalizing to average or max utility in each election.[22] He tested Random Winner, Dictatorship, FPTP, Approval, Copeland, and Borda (in increasing order of utility), with both uniform and normal utility distributions, and varying correlation, with 2–100 voters and 2–20 candidates.

Starting in 2000, Warren D. Smith (Princeton applied math PhD and founder of the Center for Range Voting) ran simulations with a somewhat different metric he called "Bayesian Regret".[12][23] This normalizes to the maximum utility candidate in each election, but not to the average utility (random winner), making it less comparable between scenarios. It is also reversed from other utility metrics: In Bayesian Regret, an impossibly perfect score would be a 0, while in SUE, an impossibly perfect score would be 100%. His unpublished[24] paper found that Range voting consistently scored as either the best method or among the best across the various conditions studied.[25] Other test results found the best method to be a range voting primary followed by a top-two general election (similar to STAR).[26][27]

In 2017, Jameson Quinn (at the time Vice-Chair of The Center for Election Science, now a statistics PhD) studied SUE under the name "Voter Satisfaction Efficiency",[28] using more complex and arguably more realistic parameters, examining a wider variety of scenarios and using a hierarchical cluster model of voter behavior. He analyzed a number of methods that had not been included in previous simulations, and his unpublished results found the best performers to be STAR voting, his own method 3-2-1 voting, Ranked pairs, or Score voting, depending on the scenario tested.[28][27]

In 2019, James Green-Armytage and Nicolaus Tideman compared utility and representativeness of the winner of various rules to select a runoff pair, finding for Condorcet methods that "the expected result with sincere voting tends to offer relatively high social welfare (though in most cases incrementally less than the utilitarian rules), and the outcomes are unlikely to be vulnerable to strategic manipulation."[29]

Strategic vulnerability
See also: Tactical voting

Another aspect which can be compared through such Monte Carlo simulations is strategic vulnerability. According to Gibbard's theorem, no deterministic voting method can be immune to strategic manipulation in all cases, but certainly some methods will have this problem more often than others. M. Balinski and R. Laraki, the inventors of the majority judgment method, performed such an investigation using a set of simulated elections based on the results from a poll of the 2007 French presidential election which they had carried out using rated ballots. Comparing range voting, Borda count, plurality voting, approval voting with two different absolute approval thresholds, Condorcet voting, and majority judgment, they found that range voting had the highest (worst) strategic vulnerability, while their own method majority judgment had the lowest (best).[30] More generally, such results on the majority judgment equally apply to other highest median rules.[31]

Balinski and Laraki also used the same information to investigate how likely it was that each of those methods, as well as runoff voting, would elect a centrist. Opinions differ on whether this is desirable or not. Some argue that methods which favor centrists are better because they are more stable; others argue that electing ideologically purer candidates gives voters more choice and a better chance to retrospectively judge the relative merits of those ideologies; while Balinski and Laraki argue that both centrist and extremist candidates should have a chance to win, to prevent forcing candidates into taking either position. According to their model, plurality, runoff voting, and approval voting with a higher approval threshold tended to elect extremists (100%, 98%, and 94% of the time, respectively); majority judgement elected both centrists and extremists (56% extremists); and range, Borda, and approval voting with a lower approval threshold elected centrists (6%; 0.25–13% depending on the number of candidates; and 6% extremists; respectively).[32] However, their model did not take into account voters' strategic reactions to the method used, such as "lesser of two evils" voting under plurality.

Tactical voting has implications for the practical social utility efficiency of a voting method. While Feddersen, Gailmard, and Sardoni find that "experimental results support the concept of bias toward unselfish outcomes in large elections,"[33] they observed what they termed ethical considerations dominating voter behavior as pivot probability decreased. This would imply that larger elections, or those perceived as having a wider margin of victory, would result in fewer tactical voters. Exit poll experiments have shown that voters tend to vote more sincerely for candidates they perceive have no chance of winning.[34] How voters precisely grade candidates is a topic that is not fully settled, although experiments show that their behavior depends on the grade scale, its length, and the possibility to give negative grades.[35] Score voting may thus yield greater support for third party and independent candidates, unless those candidates become viable.[36] These behaviors imply that voters vote tactically when they perceive that a candidate whom they prefer to that with the highest social utility can win, and vote honestly when they believe their candidate will win in spite of their honest vote.

Any ranked or cardinal rule can be made independent of Smith-dominated alternatives, and thus satisfy Condorcet, by restricting to the Smith set before applying the rule, considering higher scores as higher rankings in cardinal rules. Green-Armytage, Tideman, and Cosman find that adding a Condorcet provision to any rule cannot decrease its resistance to strategy, provided it satisfies the conditional majority determination property.[37] This is a weak property they define as "any group comprising a majority of voters is always able to cast their votes in such a way as to elect any candidate they wish, provided that the votes of the remaining minority are known to them and held constant." All rules satisfying majority also satisfy CMD. The authors state that "for any rule that possesses this property, and any election for which that rule is immune to strategy, the rule with a Condorcet provision added must also be immune to strategy." The addition of a Condorcet provision implies that when a Condorcet winner exists, the election is made immune to strategy, as Condorcet rules can only be manipulated by affecting how they resolve an election without a Condorcet winner; likewise, an independence of Smith-dominated alternatives provision does not make the election immune to strategy, but makes it immune to any strategy leveraging the existence of Smith-dominated alternatives.

Win region diagrams

Simulated elections in a one- or two-dimensional issue space can also be graphed in a way that shows which candidate would win when the electorate is centered on a given point. This visually illustrates issues like nonmonotonicity, clone-independence, and tendency to elect representative candidates vs unrepresentative extremists.[38][39][40]

"Soft" criteria

In addition to the above criteria, voting methods are judged using criteria that are not mathematically precise but are still important, such as simplicity, speed of vote-counting, the potential for fraud or disputed results, the opportunity for tactical voting or strategic nomination, and, for multiple-winner methods, the degree of proportionality produced.

The New Zealand Royal Commission on the Electoral System listed ten criteria for their evaluation of possible new electoral methods for New Zealand. These included fairness between political parties, effective representation of minority[41] or special interest groups, political integration, effective voter participation and legitimacy.

Convening a neutral body to assess methods using agreed-upon goals

The third methodology mentioned above, creating a set of imprecisely defined criteria, and then assigning a neutral body to evaluate each method according to these criteria is widely used by organizations or bodies which seek to choose a voting method, either for endorsement or adoption. For example, the Equal Vote Coalition evaluates voting methods according to five primary metrics:[42] equality, honesty, accuracy, simplicity, and expressiveness.

See also

Notes
  1. Approval fails the majority criterion because it does not always elect a candidate preferred by over half of voters; however, it always elects the candidate approved by the most voters.
  2. Condorcet, Smith and Independence of Smith-dominated alternatives criteria are incompatible with Independence of irrelevant alternatives, Consistency, Participation, Later-no-harm, Later-no-help, and Favorite betrayal criteria.
  3. In Approval, Range, and Majority Judgment, if all voters have perfect information about each other's true preferences and use rational strategy, any Majority Condorcet or Majority winner will be strategically forced – that is, win in all of one or more strong Nash equilibria. In particular if every voter knows that "A or B are the two most-likely to win" and places their "approval threshold" between the two, then the Condorcet winner, if one exists and is in the set {A,B}, will always win. These methods also satisfy the majority criterion in the weaker sense that any majority can force their candidate to win, if it so desires. Laslier, J-F (2006), "Strategic approval voting in a large electorate" (PDF), IDEP Working Papers, Marseille, France (405)
  4. Approval voting, range voting, and majority judgment satisfy IIA if it is assumed that voters rate candidates individually and independently of knowing the available alternatives in the election, using their own absolute scale. For this to hold, in some elections, some voters must use less than their full voting power or even abstain, despite having meaningful preferences among the available alternatives. If this assumption is not made, these methods fail IIA, as they become more ranked than rated methods.
  5. The original Independence of clones criterion applied only to ranked voting methods. (T. Nicolaus Tideman, "Independence of clones as a criterion for voting rules", Social Choice and Welfare Vol. 4, No. 3 (1987), pp. 185–206.) Tideman notes that "in the spirit of independence of clones", "if there were two or more candidates who were so similar that every voter would rank them as tied if given the chance to rank them [...], then the number of perfect clones present would have no effect on whether the perfect clones were in the set of winning candidates under approval voting". So, Approval Voting satisfies this mathematical criterion by definition. However, there is some disagreement about whether considerations of the voter in the process of making up his vote could be tactically influenced by clones (in a way that a voter would dispossess a candidate of his approval when a clone of him is introduced) and whether the definition of clones have to be extended to these considerations additionally to the handling of actual votes.
  6. Later-No-Harm and Later-No-Help assert that adding a later preference to a strictly ordered preference ballot should not help or harm an earlier preference. An Approval ballot records approvals but does not record explicit relative (e.g. later) preferences between approvals (while preferences exist from a voter's perspective). Meanwhile, a voter approving a less preferred candidate harms the probability of any other approved candidate winning, but does not help.
  7. If the number of candidates grows faster than the square root of the number of voters, this may not be the case, as ties at any point in the process, even between two non-viable candidates, could affect the final result. If the rule for resolving such ties involves no randomness, though, the method does pass the criterion.
  8. The number of piles that can be summed from various precincts is floor ((e−1) N!) − 1.
  9. Kemeny-Young does not pass the consistency criterion for winner, but the consistency criterion for full rankings, that is, if the electorate is divided in two parts and in both parts Kemeny-Young chooses the same ranking, Kemeny-Young will also choose that ranking for the combined electorate.
  10. Each prospective Kemeny-Young ordering has score equal to the sum of the pairwise entries that agree with it, and so the best ordering can be found using the pairwise matrix.
  11. Bucklin voting, with skipped and equal-rankings allowed, meets the same criteria as Majority Judgment; in fact, Majority Judgment may be considered a form of Bucklin voting. Without allowing equal rankings, Bucklin's criteria compliance is worse; in particular, it fails Independence of Irrelevant Alternatives, which for a ranked method like this variant is incompatible with the Majority Criterion.
  12. Majority Judgment does not always elect a candidate preferred over all others by over half of voters; however, it always elects the candidate uniquely top-rated by over half of voters.
  13. Majority Judgment may elect a candidate uniquely least-preferred by over half of voters, but it never elects the candidate uniquely bottom-rated by over half of voters.
  14. Majority Judgment fails the mutual majority criterion, but satisfies the criterion if the majority ranks the mutually favored set above a given absolute grade and all others below that grade.
  15. Balinski and Laraki, Majority Judgment's inventors, point out that it meets a weaker criterion they call "grade consistency": if two electorates give the same rating for a candidate, then so will the combined electorate. Majority Judgment explicitly requires that ratings be expressed in a "common language", that is, that each rating has an absolute meaning. They claim that this is what makes "grade consistency" significant. Balinski M, MJ; Laraki, R (2007), A theory of measuring, electing and ranking, 104, USA: National Academy of Sciences, pp. 8720–25, PMID 17496140
  16. In Majority Judgment, Ranked Pairs, and Schulze voting, there is always a regret-free semi-honest ballot for any voter, holding other ballots constant. That is, if they know enough about how others will vote (for instance, in the case of Majority Judgment, the winning candidate and their winning median score), there is always at least one way for them to participate without grading any less-preferred candidate above any more-preferred one. However, this can cease to hold if voters have insufficient information.
  17. Majority judgment can actually pass or fail reversal symmetry depending on the rounding method used to find the median when there are even numbers of voters. For instance, in a two-candidate, two-voter race, if the ratings are converted to numbers and the two central ratings are averaged, then MJ meets reversal symmetry; but if the lower one is taken, it does not, because a candidate with ["fair","fair"] would beat a candidate with ["good","poor"] with or without reversal. However, for rounding methods which do not meet reversal symmetry, the odds of breaking it are comparable to the odds of an irresolvable (tied) result; that is, vanishingly small for large numbers of voters.
  18. Majority Judgment is summable at order KN, where K, the number of ranking categories, is set beforehand.
  19. Though Majority Judgment does not pass this or similar criteria, there are other similar median methods, such as those based on Bucklin voting, which can meet a related, weaker criterion: ranking an additional candidate below the median grade (rather than your own grade) of your favorite candidate, cannot harm your favorite. Balinski, M., and R. Laraki. “A Theory of Measuring, Electing, and Ranking.” Proceedings of the National Academy of Sciences 104, no. 21 (2007): 8720.
  20. In fact, Majority Judgment ballots use ratings expressed in "common language" rather than numbers, that is, each rating has an absolute meaning.
  21. A variant of Minimax that counts only pairwise opposition, not opposition minus support, fails the Condorcet criterion and meets later-no-harm.
  22. Since plurality does not allow marking later preferences on the ballot at all, it is impossible to either harm or help a favorite candidate by marking later preferences, and so it trivially passes both Later-No-Harm and Later-No-Help. However, because it forces truncation, it shares some problems with methods that merely encourage truncation by failing Later-No-Harm. Similarly, though to a lesser degree, because it doesn't allow voters to distinguish between all but one of the candidates, it shares some problems with methods which fail Later-No-Help, which encourage voters to make such distinctions dishonestly.
  23. Once for each round.
  24. That is, second-round votes cannot help or harm candidates already eliminated.
  25. Later preferences are only possible between the two candidates who make it to the second round.
  26. STAR voting will elect a majority candidate X if X is in the runoff, and X's voters can guarantee they make the runoff by strategically giving the highest score to X and the lowest score to all opponents. However, if there are two or more opponents that get any points from X's voters, these opponents could shut X out of the runoff. Thus, STAR fails the majority criterion.
  27. As with the majority criterion, STAR voting fails the mutual majority criterion. However, the more candidates are in the mutual majority set, the greater the chance that at least one of them will be in the runoff, and thus be guaranteed to win.
  28. STAR does not define a full outcome ordering, only a winner. With any number of candidates besides 3, the winner cannot stay the same if the ballots are reversed.
  29. In STAR voting, in order for favorite betrayal to be strategically advantageous, four separate things must be true: the favorite candidate X must be in the runoff under an honest vote, X must lose the runoff under an honest vote, the betrayal beneficiary Y must not be in the runoff under an honest vote, and the Y must win the runoff under a strategic vote.
  30. Sortition, uniformly randomly chosen candidate is winner. Arbitrary winner, some external entity, not a voter, chooses the winner. These methods are not, properly speaking, voting methods at all, but are included to show that even a non-voting method can still pass some of the criteria.
  31. Random ballot, uniformly randomly chosen ballot determines winner. This and closely related methods are of mathematical interest because they are the only possible methods which are truly strategy-free, that is, your best vote will never depend on anything about the other voters. However, this method is not generally considered as a serious proposal for a practical method.

References
  1. Bowler, Shaun; Farrell, David M.; Pettit, Robin T. (2005-04-01). "Expert opinion on electoral systems: So which electoral system is "best"?". Journal of Elections, Public Opinion and Parties. 15 (1): 3–19. doi:10.1080/13689880500064544. ISSN 1745-7289.
  2. Vasiljev, Sergei (April 1, 2008), Cardinal Voting: The Way to Escape the Social Choice Impossibility, SSRN eLibrary, SSRN 1116545. Note that in practice, voters could change their votes depending on who is in the race (especially in cardinal voting methods). However, this possibility is ignored, because if it were accounted for, no deterministic method could possibly pass this criterion.
  3. Consistency implies participation, but not vice versa. For example, range voting complies with participation and consistency, but median ratings satisfies participation and fails consistency.
  4. Woodall, Douglas (December 1994), "Properties of Preferential Election Rules", Voting Matters (3)
  5. Small, Alex (August 22, 2010), Geometric construction of voting methods that protect voters' first choices, arXiv:1008.4331, Bibcode:2010arXiv1008.4331S
  6. Amy, Douglas J.; Behind the Ballot Box: A Citizen’s Guide to Voting Systems, p. 120 ISBN 0275965864
  7. Merrill, Samuel (1984). "A Comparison of Efficiency of Multicandidate Electoral Systems". American Journal of Political Science. 28 (1): 23–48. doi:10.2307/2110786. ISSN 0092-5853. JSTOR 2110786.
  8. Mueller, Dennis C. (2003). Public choice III. Cambridge: Cambridge University Press. ISBN 0-511-06504-3. OCLC 191952945.
  9. Shentrup, Clay (2007-07-07). "Voter Satisfaction Index". Center for Range Voting. Retrieved 2019-07-24. Voter satisfaction index, or "VSI" for short (also called "social utility efficiency" ... a lower number is actually better, and this can confuse people who are new to the concept. ... the utility units have an arbitrary magnitude, making it difficult to compare Bayesian regret figures
  10. Quinn, Jameson (2017-02-10). "Voter Satisfaction Efficiency FAQ". GitHub Pages. Retrieved 2019-07-24.
  11. Weber, Robert J. (September 1978). "Comparison of Public Choice Systems". Cowles Foundation Discussion Papers. Cowles Foundation for Research in Economics. No. 498.
  12. Smith, Warren D. (2006). "Bayesian Regret for dummies". RangeVoting.org. Retrieved 2021-01-31.
  13. Cooper, Alexandra L. (2001). "Nominating Presidential Candidates: The Primary Season Compared to Two Alternatives". Political Research Quarterly. 54 (4): 771–793. doi:10.2307/449234. ISSN 1065-9129.
  14. Hansen, Jeremy A (2014). "Comparing Approval At-Large to Plurality At-Large in Multi-Member Districts". Conference: Fifth International Workshop on Computational Social Choice.
  15. Diss, Mostapha; Doghmi, Ahmed (2016). "Multi-winner scoring election methods: Condorcet consistency and paradoxes". Public Choice. 169 (1–2): 97–116. doi:10.1007/s11127-016-0376-x. ISSN 0048-5829.
  16. Poundstone, William (2008), Gaming the Vote: Why Elections Aren't Fair (and What We Can Do About It), New York: Hill and Young, p. 239
  17. Smith, Warren. "Range Voting: The Best Way to Select a Leader?". Rangevoting.org. Retrieved 28 December 2020. The [Bayesian Regret] of a voting system depends not only on what voting system it is, but also on the number of voters and candidates, how the simulation makes each voter feel about each candidate, how ignorant voters are, how strategic they are versus how honest, etc.
  18. "Voter Satisfaction Efficiency (VSE) summary". Jameson Quinn. Retrieved 2021-02-04. Voter Satisfaction Efficiency, or VSE, is a measure of the quality of a election method... To calculate VSE, you simulate thousands of elections, using voters who cluster on issues in a realistic way. Since the voters are simulated, you can know exactly how satisfied they would be by each candidate; that is, how close the candidate is on the issues they care about.
  19. Black, Duncan. (1986). The Theory of Committees and Elections. Dordrecht: Springer Netherlands. pp. 180–185. ISBN 978-94-009-4225-7. OCLC 851382489. a single voter … attributes a certain measurable merit to the candidate of his first choice, some lesser (measurable) merit to the candidate whom he places second … Now the candidate who ought to be elected, Laplace postulates, is that one to whom most merit is attributed by the group of voters.
  20. Pivato, Marcus (2016-06-01). "Asymptotic utilitarianism in scoring rules". Social Choice and Welfare. 47 (2): 431–458. doi:10.1007/s00355-016-0971-2. ISSN 0176-1714.
  21. Merrill, Samuel (1984). "A Comparison of Efficiency of Multicandidate Electoral Systems". American Journal of Political Science. 28 (1): 23–48. doi:10.2307/2110786. ISSN 0092-5853. JSTOR 2110786.
  22. Bordley, Robert F. (1983). "A Pragmatic Method for Evaluating Election Schemes through Simulation". The American Political Science Review. 77 (1): 123–141. doi:10.2307/1956015. ISSN 0003-0554.
  23. WDS, "Appendix" (PDF), Range vote (unpublished paper), Temple, archived from the original (PDF) on March 26, 2009
  24. Poundstone 2008, p. 257: "Range voting is still largely a samizdat enterprise on the fringes of social choice theory. The most glaring example must be Smith's pivotal 2000 paper. It has never been published in a journal."
  25. Poundstone 2008, p. 240.
  26. Smith, Warren D. (2007). "Range voting with mixtures of honest and strategic voters". RangeVoting.org. Retrieved 2021-02-03. Range2Runoff 0.15947
  27. Frohnmayer, Mark. "The Election Science Behind the Reform Movement". Equal Vote. Retrieved 28 December 2020.
  28. "Voter Satisfaction Efficiency (VSE) FAQ". Jameson Quinn. Retrieved 2021-02-03.
  29. Green-Armytage, James; Tideman, T. Nicolaus (2019-05-27). "Selecting the Runoff Pair" (PDF). Public Choice. Retrieved 2021-02-04.
  30. Balinski, M; Laraki, R (2011) [2007], "Election by Majority Judgement: Experimental Evidence", in Dolez, Bernard; Grofman, Bernard; Laurent, Annie (eds.), In Situ and Laboratory Experiments on Electoral Law Reform: French Presidential Elections, Springer
  31. Fabre, Adrien (2020). "Tie-breaking the Highest Median: Alternatives to the Majority Judgment" (PDF). Social Choice and Welfare. doi:10.1007/s00355-020-01269-9.
  32. Balinski & Laraki 2007.
  33. Feddersen, Timothy; Gailmard, Sean; Sandroni, Alvaro (2009). "Moral Bias in Large Elections: Theory and Experimental Evidence". The American Political Science Review. 103 (2): 175–192. doi:10.1017/S0003055409090224. JSTOR 27798496.
  34. "Honesty and Strategy in real-world voters". The center for range voting.
  35. Baujard, Antoinette; Igersheim, Herrade; Lebon, Isabelle; Gavrel, Frédéric; Laslier, Jean-François (2014). "How voters use grade scales in evaluative voting" (PDF). European Journal of Political Economy. 55: 14–28. doi:10.1016/j.ejpoleco.2017.09.006.
  36. "The "Nursery Effect" (Executive summary)". The center for range voting.
  37. Green-Armytage, James; Tideman, T. Nicolaus; Cosman, Rafael (2015-08-11). "Statistical evaluation of voting rules". Social Choice and Welfare. Springer Science and Business Media LLC. 46 (1): 183–212. doi:10.1007/s00355-015-0909-0. ISSN 0176-1714.
  38. These two-dimensional graphs are called Yee diagrams after their inventor, Ka-Ping Yee. His website includes some sample graphs. Yee also produced the Voteline simulator, which shows one-dimensional win region bars.
  39. "Yee diagram". Electowiki. 2020-08-03. Retrieved 2021-02-03.
  40. "Animated Voting Methods".
  41. The ballot limited designation is technically possible only if the members of the majority, dividing their votes, cannot determine, individually, the minority appointment: Buonomo, Giampiero (2001). "L''emicollegio' sceglie il rappresentante di minoranza (o di maggioranza)". Diritto&Giustizia Edizione Online.  – via Questia (subscription required)
  42. Frohnmayer, Mark. "Comparing STAR Voting and Ranked Choice". Equal Vote. Retrieved 28 December 2020.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.