Ductility
Ductility is a mechanical property commonly described as a material's amenability to drawing (e.g. into wire).[1] In materials science, ductility is defined by the degree to which a material can sustain plastic deformation under tensile stress before failure.[2][3] Ductility is an important consideration in engineering and manufacturing, defining a material's suitability for certain manufacturing operations (such as cold working) and its capacity to absorb mechanical overload.[4] Materials that are generally described as ductile include gold and copper.[5]


Malleability, a similar mechanical property, is characterized by a material's ability to deform plastically without failure under compressive stress.[6][7] Historically, materials were considered malleable if they were amenable to forming by hammering or rolling.[1] Lead is an example of a material which is, relatively, malleable but not ductile.[5][8]
Materials science
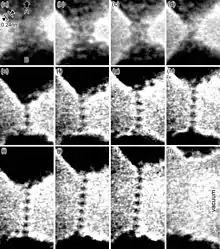
Ductility is especially important in metalworking, as materials that crack, break or shatter under stress cannot be manipulated using metal-forming processes such as hammering, rolling, drawing or extruding. Malleable materials can be formed cold using stamping or pressing, whereas brittle materials may be cast or thermoformed.
High degrees of ductility occur due to metallic bonds, which are found predominantly in metals; this leads to the common perception that metals are ductile in general. In metallic bonds valence shell electrons are delocalized and shared between many atoms. The delocalized electrons allow metal atoms to slide past one another without being subjected to strong repulsive forces that would cause other materials to shatter.
The ductility of steel varies depending on the alloying constituents. Increasing the levels of carbon decreases ductility. Many plastics and amorphous solids, such as Play-Doh, are also malleable. The most ductile metal is platinum and the most malleable metal is gold.[10][11] When highly stretched, such metals distort via formation, reorientation and migration of dislocations and crystal twins without noticeable hardening.[12]
Quantification of ductility
The quantities commonly used to define ductility in a tension test are percent elongation (sometimes denoted as ) and reduction of area (sometimes denoted as ) at fracture.[13] Fracture strain is the engineering strain at which a test specimen fractures during a uniaxial tensile test. Percent elongation, or engineering strain at fracture, can be written as: [14][15][16]
Percent reduction in area can be written as: [14][15][16]
where the area of concern is the cross-sectional area of the gage of the specimen.
According to Shigley's Mechanical Engineering Design [17] significant denotes about 5.0 percent elongation.
Ductile–brittle transition temperature
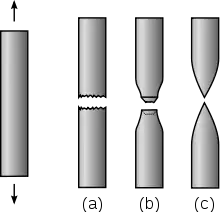
(a) Brittle fracture
(b) Ductile fracture
(c) Completely ductile fracture
The ductile–brittle transition temperature (DBTT), nil ductility temperature (NDT), or nil ductility transition temperature of a metal is the temperature at which the fracture energy passes below a predetermined value (for steels typically 40 J[18] for a standard Charpy impact test). DBTT is important since, once a material is cooled below the DBTT, it has a much greater tendency to shatter on impact instead of bending or deforming (low temperature embrittlement). For example, zamak 3 exhibits good ductility at room temperature but shatters when impacted at sub-zero temperatures. DBTT is a very important consideration in selecting materials that are subjected to mechanical stresses. A similar phenomenon, the glass transition temperature, occurs with glasses and polymers, although the mechanism is different in these amorphous materials.
In some materials, the transition is sharper than others and typically requires a temperature-sensitive deformation mechanism. For example, in materials with a body-centered cubic (bcc) lattice the DBTT is readily apparent, as the motion of screw dislocations is very temperature sensitive because the rearrangement of the dislocation core prior to slip requires thermal activation. This can be problematic for steels with a high ferrite content. This famously resulted in serious hull cracking in Liberty ships in colder waters during World War II, causing many sinkings. DBTT can also be influenced by external factors such as neutron radiation, which leads to an increase in internal lattice defects and a corresponding decrease in ductility and increase in DBTT.
The most accurate method of measuring the DBTT of a material is by fracture testing. Typically four point bend testing at a range of temperatures is performed on pre-cracked bars of polished material.
For experiments conducted at higher temperatures, dislocation activity increases. At a certain temperature, dislocations shield the crack tip to such an extent that the applied deformation rate is not sufficient for the stress intensity at the crack-tip to reach the critical value for fracture (KiC). The temperature at which this occurs is the ductile–brittle transition temperature. If experiments are performed at a higher strain rate, more dislocation shielding is required to prevent brittle fracture, and the transition temperature is raised.
See also
- Deformation
- Work hardening, which improves ductility in uniaxial tension by delaying the onset of instability
- Strength of materials
References
- Brande, William Thomas (1853). A Dictionary of Science, Literature, and Art: Comprising the History, Description, and Scientific Principles of Every Branch of Human Knowledge : with the Derivation and Definition of All the Terms in General Use. Harper & Brothers. p. 369.
- Kalpakjian, Serope, 1928- (1984). Manufacturing processes for engineering materials. Reading, Mass.: Addison-Wesley. p. 30. ISBN 0-201-11690-1. OCLC 9783323.CS1 maint: multiple names: authors list (link)
- "Ductility - What is Ductile Material". Nuclear Power. Retrieved 2020-11-14.
- Budynas, Richard G. (2015). Shigley's Mechanical Engineering Design—10th ed. McGraw Hill. p. 233. ISBN 978-0-07-339820-4..
- Chandler Roberts-Austen, William (1894). An Introduction to the Study of Metallurgy. London: C. Griffin. p. 16.
- "Malleability - Malleable Materials". Nuclear Power. Archived from the original on 2020-09-25. Retrieved 2020-11-14.
- DOE FUNDAMENTALS HANDBOOK MATERIAL SCIENCE. Volume 1, Module 2 – Properties of Metals. U.S. Department of Energy. January 1993. p. 25.
- Rich, Jack C. (1988). The Materials and Methods of Sculpture. Courier Dover Publications. p. 129. ISBN 978-0-486-25742-6..
- Masuda, Hideki (2016). "Combined Transmission Electron Microscopy – In situ Observation of the Formation Process and Measurement of Physical Properties for Single Atomic-Sized Metallic Wires". In Janecek, Milos; Kral, Robert (eds.). Modern Electron Microscopy in Physical and Life Sciences. InTech. doi:10.5772/62288. ISBN 978-953-51-2252-4.
- Vaccaro, John (2002) Materials handbook, Mc Graw-Hill handbooks, 15th ed.
- Schwartz, M. (2002) CRC encyclopedia of materials parts and finishes, 2nd ed.
- Lah, Che; Akmal, Nurul; Trigueros, Sonia (2019). "Synthesis and modelling of the mechanical properties of Ag, Au and Cu nanowires". Sci. Technol. Adv. Mater. 20 (1): 225–261. Bibcode:2019STAdM..20..225L. doi:10.1080/14686996.2019.1585145. PMC 6442207. PMID 30956731.
- Dieter, G. (1986) Mechanical Metallurgy, McGraw-Hill, ISBN 978-0-07-016893-0
- "Ductility Review - Strength Mechanics of Materials - Engineers Edge". www.engineersedge.com. Retrieved 2020-07-14.
- Askeland, Donald R. (2016). "6-4 Properties Obtained from the Tensile Test". The science and engineering of materials. Wright, Wendelin J. (Seventh ed.). Boston, MA. p. 195. ISBN 978-1-305-07676-1. OCLC 903959750.
- Callister, William D., Jr. (2010). "6.6 Tensile Properties". Materials science and engineering : an introduction. Rethwisch, David G. (8th ed.). Hoboken, NJ. p. 166. ISBN 978-0-470-41997-7. OCLC 401168960.
- Budynas, Richard G. (2015). Shigley's Mechanical Engineering Design—10th ed. McGraw Hill. p. 233. ISBN 978-0-07-339820-4..
- John, Vernon (1992). Introduction to Engineering Materials, 3rd ed. New York: Industrial Press. ISBN 0-8311-3043-1.
External links
| Look up ductility in Wiktionary, the free dictionary. |
| Look up malleability in Wiktionary, the free dictionary. |