Gömböc

If analyzed quantitatively in terms of flatness and thickness, the discovered mono-monostatic body (defined in §History) is the most sphere-like, apart from the sphere itself. Because of this, it was named gömböc, a diminutive form of gömb ("sphere" in Hungarian). The word gömböc referred originally to a sausage-like food: seasoned pork filled in pig-stomach, similar to haggis. There is a Hungarian folk tale about an anthropomorphic gömböc that swallows several people whole.[8]

When a roly-poly toy is pushed, the height of the center of mass rises from the green line to the orange line, and the center of mass is no longer over the point of contact with the ground.

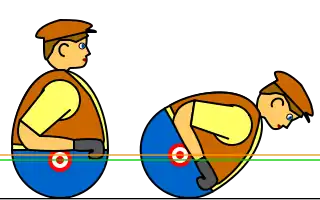
In geometry, a body with a single stable resting position is called monostatic, and the term mono-monostatic has been coined to describe a body which additionally has only one unstable point of balance. (The previously known monostatic polyhedron does not qualify, as it has three unstable equilibria.) A sphere weighted so that its center of mass is shifted from the geometrical center is a mono-monostatic body. A more common example is the Comeback Kid, Weeble or roly-poly toy (see left figure). Not only does it have a low center of mass, but it also has a specific shape. At equilibrium, the center of mass and the contact point are on the line perpendicular to the ground. When the toy is pushed, its center of mass rises and also shifts away from that line. This produces a righting moment which returns the toy to the equilibrium position.

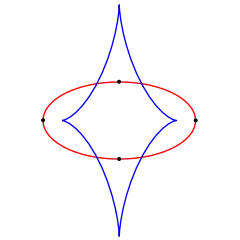
The above examples of mono-monostatic objects are necessarily inhomogeneous, that is, the density of their material varies across their body. The question of whether it is possible to construct a three-dimensional body which is mono-monostatic but also homogeneous and convex was raised by Russian mathematician Vladimir Arnold in 1995. The requirement of being convex is essential as it is trivial to construct a mono-monostatic non-convex body (an example would be a ball with a cavity inside it). Convex means that a straight line between any two points on a body lies inside the body, or, in other words, that the surface has no sunken regions but instead bulges outward (or is at least flat) at every point. It was already well known, from a geometrical and topological generalization of the classical four-vertex theorem, that a plane curve has at least four extrema of curvature, specifically, at least two local maxima and at least two local minima (see right figure), meaning that a (convex) mono-monostatic object does not exist in two dimensions. Whereas a common anticipation was that a three-dimensional body should also have at least four extrema, Arnold conjectured that this number could be smaller.[9]

An ellipse (red) and its evolute (blue), showing the four vertices of the curve. Each vertex corresponds to a cusp on the evolute.

The characteristic shape of the gömböc

The problem was solved in 2006 by Gábor Domokos and Péter Várkonyi. Domokos is an engineer and is the head of Mechanics, Materials and Structures at Budapest University of Technology and Economics. Since 2004, he has been the youngest member of the Hungarian Academy of Sciences. Várkonyi was trained as an architect; he was a student of Domokos and a silver medalist at the International Physics Olympiad in 1997. After staying as a postdoctoral researcher at Princeton University in 2006–2007, he assumed an assistant professor position at Budapest University of Technology and Economics.[9][10] Domokos had previously been working on mono-monostatic bodies. In 1995 he met Arnold at a major mathematics conference in Hamburg, where Arnold presented a plenary talk illustrating that most geometrical problems have four solutions or extremal points. In a personal discussion, however, Arnold questioned whether four is a requirement for mono-monostatic bodies and encouraged Domokos to seek examples with fewer equilibria.[11]

The rigorous proof of the solution can be found in references of their work.[9] The summary of the results is that the three-dimensional homogeneous convex (mono-monostatic) body, which has one stable and one unstable equilibrium point, does exist and is not unique. Such bodies are hard to visualize, describe or identify. Their form is dissimilar to any typical representative of any other equilibrium geometrical class. They should have minimal "flatness", and, to avoid having two unstable equilibria, must also have minimal "thinness". They are the only non-degenerate objects having simultaneously minimal flatness and thinness. The shape of those bodies is very sensitive to small variation, outside which it is no longer mono-monostatic. For example, the first solution of Domokos and Várkonyi closely resembled a sphere, with a shape deviation of only 10⁻⁵. It was dismissed, as it was extremely hard to test experimentally.[12] Their published solution was less sensitive; yet it has a shape tolerance of 10⁻³, that is 0.1 mm for a 10 cm size.[13]

Domokos and his wife developed a classification system for shapes based on their points of equilibrium by analyzing pebbles and noting their equilibrium points.[14] In one experiment, they tried 2,000 pebbles collected on the beaches of the Greek island of Rhodes and found not a single mono-monostatic body among them, illustrating the difficulty of finding or constructing such a body.[9][12]

The solution of Domokos and Várkonyi has curved edges and resembles a sphere with a squashed top. In the top figure, it rests in its stable equilibrium. Its unstable equilibrium position is obtained by rotating the figure 180° about a horizontal axis. Theoretically, it will rest there, but the smallest perturbation will bring it back to the stable point. The mathematical gömböc has sphere-like properties. In particular, its flatness and thinness are minimal, and this is the only type of nondegenerate object with this property.[9] Domokos and Várkonyi are interested to find a polyhedral solution with the surface consisting of a minimal number of flat planes. There is a prize [15] to anyone who finds the minimal respective numbers F,E,V of faces, edges and vertices for such a polyhedron, which amounts to $1,000,000 divided by the number C=F+E+V-2, which is called the mechanical complexity of mono-monostatic polyhedra. Obviously, one can approximate a curvilinear gömböc with a finite number of discrete surfaces; however, their estimate is that it would take thousands of planes to achieve that. They hope, by offering this prize, to stimulate finding a radically different solution from their own.[4]

The shape of the Indian star tortoise resembles a gömböc. This tortoise rolls easily without relying much on its limbs.

The balancing properties of the gömböc are associated with the "righting response" ⁠— the ability to turn back when placed upside down⁠ ⁠— of shelled animals such as tortoises and beetles. This may happen in a fight or predator attack and is crucial for their survival. The presence of only one stable and unstable point in a gömböc means that it would return to one equilibrium position no matter how it is pushed or turned around. Whereas relatively flat animals (such as beetles) heavily rely on momentum and thrust developed by moving their limbs and wings, the limbs of many dome-shaped tortoises are too short to be of use in righting themselves.

Domokos and Várkonyi spent a year measuring tortoises in the Budapest Zoo, Hungarian Museum of Natural History and various pet shops in Budapest, digitizing and analyzing their shells, and attempting to "explain" their body shapes and functions from their geometry work. Their first biology paper was rejected five times, but finally accepted by the biology journal Proceedings of the Royal Society.[1] It was then immediately popularized in several science news reports, including the science journals Nature[3] and Science.[4][16] The reported model can be summarized as flat shells in tortoises are advantageous for swimming and digging. However, the sharp shell edges hinder the rolling. Those tortoises usually have long legs and neck and actively use them to push the ground, in order to return to the normal position if placed upside down. On the contrary, "rounder" tortoises easily roll on their own; those have shorter limbs and use them little when recovering lost balance. (Some limb movement would always be needed because of imperfect shell shape, ground conditions, etc.) Round shells also resist better the crushing jaws of a predator and are better for thermal regulation.[1][2][3][4]

The Argentine snake-necked turtle is an example of a flat turtle, which relies on its long neck and legs to turn over when placed upside down.

The explanation of tortoise body shape, using the gömböc theory, has already been accepted by some biologists. For example, Robert McNeill Alexander, one of the pioneers of modern biomechanics, used it in his plenary lecture on optimization in evolution in 2008.[17]

The gömböc has motivated research about the evolution of natural shapes: while gömböc-shaped pebbles are rare, the connection between geometric shape and the number of static balance points appears to be a key to understand natural shape evolution:[18] both experimental and numerical evidence indicates that the number N of static equilibrium points of sedimentary particles is being reduced in natural abrasion. This observation helped to identify the geometric partial differential equations governing this process and these models provided key evidence not only on the provenance of Martian pebbles,[19] but also on the shape of the interstellar asteroid ʻOumuamua.[20]

Although both chipping by collisions and frictional abrasion gradually eliminates balance points, still, shapes stop short of becoming a Gömböc; the latter, having N=2 balance points, appears as an unattainable end point of this natural process. The likewise invisible starting point appears to be the cube with N=26 balance points, confirming a postulate by Plato who identified the four classical elements and the cosmos with the five Platonic solids, in particular, he identified the element Earth with the cube. While this claim has been viewed for a long time only as a metaphor, recent research [21] proved that it is qualitatively correct: the most generic fragmentation patterns in nature produce fragments which can be approximated by polyhedra and the respective statistical averages for the numbers of faces, vertices, and edges are 6, 8, and 12, respectively, agreeing with the corresponding values of the cube. This is well reflected in the allegory of the cave, where Plato explains that the immediately visible physical world (in the current example, the shape of individual natural fragments) may only be a distorted shadow of the true essence of the phenomenon, an idea (in the current example, the cube).

This result was broadly reported on by leading popular science journals, including Science,[22] Popular Mechanics,[23] Quanta,[24] Wired,[25] Futura-Sciences, [26] the Italian edition of Scientific American [27] and the Greek daily journal To Vima.[28] In 2020, Science put this research among the top 10 most interesting articles of the year [29] and in the "Breakthrough of the Year, top online news, and science book highlights" podcast [30] news editor David Grimm discussed it with host Sarah Crespi among the 4 most notable research items, calling it the most philosophical paper, by far.[31]

Due to their vicinity to the sphere, all mono-monostatic shapes have very small tolerance for imperfections and even for the physical gömböc design this tolerance is daunting (<0.01%). Nevertheless, if we drop the requirement of homogeneity, the gömböc design serves as a good starting geometry if we want to find the optimal shape for self-righting objects carrying bottom weights. This inspired a team of engineers led by Vijay Kumar at the University of Pennsylvania [32] to design gömböc-like cages for drones exposed to mid-air collisions. A team led by Robert S. Langer from the Massachusetts Institute of Technology and Harvard University proposed[33] a Gömböc-inspired capsule that releases insulin in the stomach and could replace injections for patients with type-1 diabetes. The key element of the new capsule is its ability to find a unique position in the stomach, and this ability is based on its bottom weight and its overall geometry, optimized for self-righting. According to the article, after studying the papers on the gömböc[9] and the geometry of turtles,[1] the authors ran an optimization, which produced a mono-monostatic capsule with a contour almost identical to the frontal view of the gömböc. When competing for the 2017 America's Cup the Emirates Team New Zealand developed a simulation software to optimize the performance of their AC50 catamaran and decided to christen the software "Gomboc" in reference to the desired mono-stable balance of the boat as well to honor similar optimization efforts dedicated to the development of the Gömböc shape.[34] The Gömböc software is fast becoming the standard tool of naval architects for all performance boats.[35]

The strict shape tolerance of gömböcs hindered production. The first prototype of a gömböc was manufactured in summer 2006 using three-dimensional rapid prototyping technology. Its accuracy, however, was below requirements, and the gömböc would often get stuck in an intermediate position rather than returning to the stable equilibrium. The technology was improved by using numerical control milling to increase the spatial accuracy to the required level and to use various construction materials. In particular, transparent (especially lightly colored) solids are visually appealing, as they demonstrate the homogeneous composition. Current materials for gömböcs include various metals and alloys, plastics such as Plexiglass. Beyond computer-controlled milling, a special hybrid technology (using milling and molding) has been developed to produce functional but light and more affordable gömböc models.[36] The balancing properties of a gömböc are affected by mechanical defects and dust both on its body and on the surface on which it rests. If damaged, the process of restoring the original shape is more complex than producing a new one.[37] Although in theory the balancing properties should not depend on the material and object size, in practice, both larger and heavier gömböcs have better chances to return to equilibrium in case of defects.[38]

This is a map showing individual gömböc models around the world. By clicking this link you can view the interactive version of this map.

In 2007, a series of individual gömböc models has been launched. These models carry a unique number N in the range 1 ≤ N ≤ Y where Y denotes the current year. Each number is produced only once, however, the order of production is not according to N, rather, at request. Initially these models were produced by rapid prototyping, with the serial number appearing inside, printed with a different material having the same density. Now all individual models are made by Numerical control (CNC) machining and the production process of each individual gömböc model includes the manufacturing of individual tools which are subsequently discarded. The first individually numbered Gömböc model (Gömböc 001) was presented by Domokos and Várkonyi as a gift to Vladimir Arnold on occasion of his 70th birthday.[39] and Professor Arnold later donated this piece to the Steklov Institute of Mathematics where it is on exhibit. While the majority of the existing numbered pieces are owned by private individuals, many pieces are public at renowned institutions worldwide.

There are two types of gömböc models which do not carry a serial number. Eleven pieces were manufactured for the World Expo 2010, and the logo of the Hungarian Pavilion was engraved into these pieces. The other non-numbered type of individual gömböc models are the insignia of the Stephen Smale Prize in Mathematics, awarded by the Foundations of Computational Mathematics every third year.

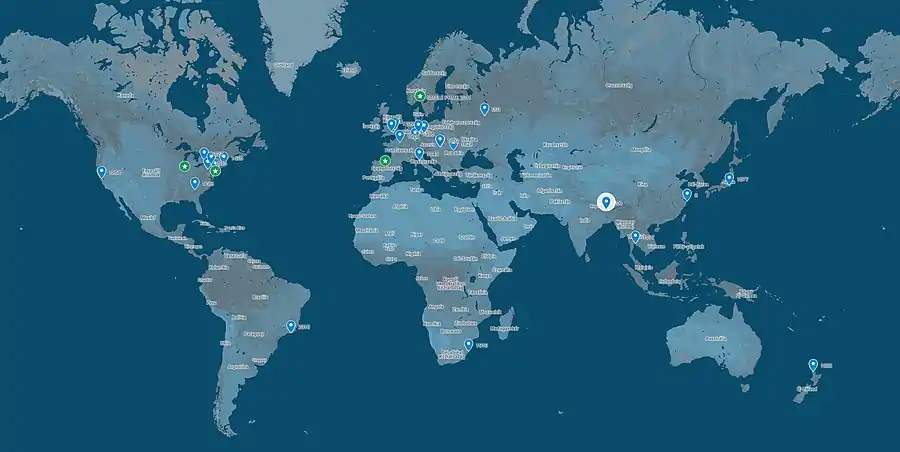
For more information on individual Gömböc pieces see the table below, click on the interactive version of the accompanying map or see the online booklet.[40]

Serial number	Institution	Location	Number's explanation	Date of exhibit	Technology	Material	Height (mm)	Link to more detail	Other comments
1	Steklov Institute of Mathematics	Moscow, Russia	First-ever numbered gömböc	Aug 2007	Rapid prototyping	Plastic	85	Picture of exhibit	Gift of Vladimir Arnold
8	Hungarian Pavilion	Dinghai, China	The number 8 is considered as a lucky number in Chinese numerology	Dec 2017	assembled from CNC-made parts	Plexiglass	500	Picture of exhibit View of pavilion	First on exhibit at the World Expo 2010
13	Windsor Castle	Windsor, Berkshire, United Kingdom		Feb 2017	CNC	99.99% certified silver	90	Picture of exhibit	Sponsored by Ottó Albrecht
108	Residence of the Shamarpa	Kalimpong, India	The number of volumes of the Kangyur, containing the teachings of Buddha	Feb 2008	CNC	AlMgSi alloy	90	Pictures of the event of donation	Gift of the Kamala Buddhist Community
400	New College, Oxford	Oxford, United Kingdom	Anniversary of the foundation of the chair for the Savilian Professor of Geometry	Nov 2019	CNC	Bronze	90	Picture of exhibit	Sponsored by Ottó Albrecht
1209	University of Cambridge	Cambridge, United Kingdom	Year of foundation	Jan 2009	CNC	AlMgSi alloy	90	Catalog of the Whipple Museum	Part of the Whipple Collection. Gift of the inventors
1343	University of Pisa	Pisa, Italy	Year of foundation	Apr 2019	CNC	AlMgSi alloy	90	Picture of exhibit	Sponsored by Ottó Albrecht
1348	Windsor Castle	Windsor, Berkshire, United Kingdom	Year of foundation of the Order of the Garter	Feb 2017	CNC	Clear plexiglass	180	Picture of ceremony	Sponsored by Ottó Albrecht
1386	University of Heidelberg	Heidelberg, Germany	Year of foundation	Jul 2019	CNC	Clear plexiglass	180	Picture of exhibit	Sponsored by Ottó Albrecht
1409	Leipzig University	Leipzig, Germany	Year of foundation	Dec 2014	CNC	AlMgSi alloy	90	Picture of exhibit	Sponsored by Ottó Albrecht
1546	Trinity College, Cambridge	Cambridge, United Kingdom	Year of foundation	Dec 2008	CNC	AlMgSi alloy	90	Picture of exhibit	Gift of Domokos
1636	Harvard University	Boston, Massachusetts, United States	Year of foundation	Jun 2019	CNC	AlMgSi alloy	90	Picture of exhibit	Part of the Mathematical Model Collection
1737	University of Göttingen	Göttingen, Germany	Year of foundation	Oct 2012	CNC	AlMgSi alloy	90	Picture of exhibit	Part of the Mathematical Model Collection
1740	University of Pennsylvania	Philadelphia, Pennsylvania, United States	Year of foundation	Dec 2020	CNC	AlMgSi alloy	90	Picture of exhibit	Sponsored by Ottó Albrecht
1746	Princeton University	Princeton, New Jersey, United States	Year of foundation	Jul 2016	CNC	Clear plexiglass	180	Picture of exhibit	Sponsored by Ottó Albrecht
1785	University of Georgia	Athens, Georgia, United States	Year of foundation	Jan 2017	CNC	AlMgSi alloy	90	Picture of exhibit	Sponsored by Ottó Albrecht
1802	Hungarian National Museum	Budapest, Hungary	Year of foundation	Mar 2012	CNC	Clear plexiglass	195	Picture of exhibit	Sponsored by Thomas Cholnoky
1821	Crown Estate	London, United Kingdom	Year of invention of the electric motor by Michael Faraday	May 2012	CNC	AlMgSi alloy	90	Picture of ceremony	Environmental Safety Prize awarded to E.ON Climate and Renewables
1823	Bolyai Museum, Teleki Library	Romania Târgu Mureș, Romania	Year of the Temesvár Letter by János Bolyai when he announced his discovery of non-Euclidean geometry	Oct 2012	CNC	AlMgSi alloy	90	Picture of exhibit	Sponsored by Ottó Albrecht
1825	Hungarian Academy of Sciences	Budapest, Hungary	Year of foundation	Oct 2009	CNC	AlMgSi alloy	180	Picture of exhibit	On exhibit in the Academy's main building
1827	University of Toronto	Toronto, Ontario, Canada	Year of foundation	Jun 2019	CNC	AlMgSi alloy	90	Picture of exhibit	Part of the Mathematical Collection. Sponsored by Ottó Albrecht
1828	Technical University of Dresden	Dresden, Saxony, Germany	Year of foundation	Jun 2020	CNC	AlMgSi alloy	90	Picture of exhibit	Part of the Digital Archive of Mathematical Models (DAMM) . Sponsored by Ottó Albrecht
1837	National and Kapodistrian University of Athens	Athens, Greece	Year of foundation	Dec 2019	CNC	AlMgSi alloy	90	Picture of exhibit	Gift of the Hungarian Embassy
1855	Pennsylvania State University	College Park, Pennsylvania, United States	Year of foundation	Sep 2015	CNC	AlMgSi alloy	90	Picture of exhibit	Sponsored by Ottó Albrecht
1865	Cornell University	Ithaca, New York, United States	Year of foundation	Sep 2018	CNC	AlMgSi alloy	90	Picture of exhibit	Gift of Domokos
1868	University of California, Berkeley	Berkeley, California, United States	Year of foundation	Nov 2018	CNC	AlMgSi alloy	90	Picture of exhibit	Sponsored by Ottó Albrecht
1877	University of Tokyo	Tokyo, Japan	Year of foundation	Aug 2018	CNC	AlMgSi alloy	90	Picture of exhibit	Part of the Mathematical Model Collection. Sponsored by Ottó Albrecht
1883	University of Auckland	Auckland, New Zealand	Year of foundation	Feb 2017	CNC	Titanium	90	Picture of exhibit
1893	Sobolev Institute of Mathematics	Novosibirsk, Russia	Year of foundation of the city of Novosibirsk	Dec 2019	CNC	AlMgSi alloy	90	Picture of exhibit	Sponsored by Ottó Albrecht
1896	Hungarian Patent Office	Budapest, Hungary	Year of foundation	Nov 2007	Rapid prototyping	Plastic	85	Picture of exhibit
1910	University of KwaZulu-Natal	Durban, South Africa	Year of foundation	Oct 2015	CNC	AlMgSi alloy	90	Picture of exhibit	Sponsored by Ottó Albrecht, presented by Hungarian ambassador András Király.
1911	University of Regina	Regina, Saskatchewan, Canada	Year of foundation	Mar 2020	CNC	AlMgSi alloy	90	Picture of exhibit	Sponsored by Ottó Albrecht
1917	Chulalongkorn University	Bangkok, Thailand	Year of foundation	Mar 2018	CNC	AlMgSi alloy	90	Picture of exhibit	Gift of the Hungarian Embassy
1924	Hungarian National Bank	Budapest, Hungary	Year of foundation	Aug 2008	CNC	AlMgSi alloy	180	Picture of exhibit
1928	Institut Henri Poincaré	Paris, France	Year of foundation	Apr 2011	CNC	AlMgSi alloy	90	Picture of exhibit	Part of the Mathematical Model Collection
1930	Moscow Power Engineering Institute	Moscow, Russia	Year of foundation	Dec 2020	CNC	AlMgSi alloy	90	Picture of exhibit	Gift of the Hungarian Embassy and the Hungarian Cultural Institute in Moscow.
1978	University of Tromsø - The Arctic University of Norway	Tromsø, Norway	Year of foundation of the Department of Mathematics	Aug 2020	CNC	AlMgSi alloy	90	Picture of exhibit	Part of the Mathematical Model Collection. Sponsored by Ottó Albrecht.
1996	University of Buenos Aires	Buenos Aires, Argentina	Year of naming the Physics Department after Juan José Giambiagi	Mar 2020	CNC	AlMgSi alloy	90	Picture of exhibit	Sponsored by Ottó Albrecht, presented by Hungarian ambassador Csaba Gelényi.
2013	University of Oxford	Oxford, United Kingdom	Year of opening of the Andrew Wiles Mathematical Building	Feb 2014	CNC	Stainless steel	180	Picture of exhibit	Sponsored by Tim Wong and Ottó Albrecht
2016	University of Auckland	Auckland, New Zealand	Year of opening of the Science Center	Feb 2017	CNC	Clear Plexiglass	180	Picture of exhibit
2018	Instituto Nacional de Matemática Pura e Aplicada	Rio de Janeiro, Brazil	Year of the International Congress of Mathematicians held in Rio de Janeiro	Oct 2018	CNC	AlMgSi alloy	90	Picture of exhibit	Sponsored by Ottó Albrecht

The gömböc has inspired a number of artists.

The award-winning short movie Gömböc (2010), directed by Ulrike Vahl, is a character sketch about four misfits who fight with everyday setbacks and barriers and who have one thing in common: if they fall down, then they rise again.[41]

The short film "The Beauty of Thinking" (2012), directed by Márton Szirmai, was a finalist at the GE Focus Forward festival. It tells the story of the discovery of the gömböc.[42][43]

The characteristic shape of the gömböc is curiously reflected in the critically acclaimed novel Climbing Days (2016) by Dan Richards as he describes scenery: "All over Montserrat the landscape reared as gömböc domes and pillars."[44]

A recent solo exhibition of conceptual artist Ryan Gander evolved around the theme of self-righting and featured seven large gömböc shapes gradually covered by black volcanic sand.[45]

The gömböc has also appeared around the globe in art galleries as a recurrent motive in the paintings of Vivien Zhang.[46]

In the fall of 2020, the Korzo Theatre [47] in The Hague and the Theatre Municipal in Biarritz presented the solo dance production "Gömböc" [48] by French choreographer Antonin Comestaz [49]

The invention of the gömböc has been in the focus of public and media attention, repeating the success of another Hungarian Ernő Rubik when he designed his cube-shaped puzzle in 1974.[50] For their discovery, Domokos and Várkonyi were decorated with the Knight's Cross of the Republic of Hungary.[51] The New York Times Magazine selected the gömböc as one of the 70 most interesting ideas of the year 2007.[52][53]

The Stamp News website[54] shows the new stamps issued on 30 April 2010, by Hungary, which illustrate a gömböc in different positions. The stamp booklets are arranged in such a manner that the gömböc appears to come to life when the booklet is flipped. The stamps were issued in association with the gömböc on display at the World Expo 2010 (1 May to 31 October). This was also covered by the Linn's Stamp News magazine.[55]

The Gömböc appeared in the July 12th 2009 episode of the QI series on BBC with host Stephen Fry and it also appeared on the US quiz show Jeopardy with host Alex Trebek, on October 1st 2020 .

In the internet series Video Game High School, an anthropomorphized gömböc is the antagonist of a children's game being made by the character Ki Swan in the Season 1 episode "Any Game In The House".

The role playing game webcomic Darths and Droids featured (but did not picture) a gömböc as a one-sided die in September 2018.

• Instability
• Monostatic polytope
• Self-righting watercraft

• Non-technical description of development, with short video
• Expo 2010 presentation of a gömböc with lots of photos