Garbled circuit

In the garbled circuit protocol, we make use of oblivious transfer. In the oblivious transfer, a string is transferred between a sender and a receiver in the following way: a sender has two strings ${\displaystyle S_{0}}$ and ${\displaystyle S_{1}}$. The receiver chooses ${\displaystyle i\in \{0,1\}}$ and the sender sends ${\displaystyle S_{i}}$ with the oblivious transfer protocol such that

1. the receiver doesn't get any information about ${\displaystyle S_{(1-i)}}$,
2. the value of ${\displaystyle i}$ is not exposed to the sender.

Note that while the receiver doesn't know the ${\displaystyle S_{0},S_{1}}$ values, in practice the receiver knows some information about what ${\displaystyle S_{i}}$ encodes so that the receiver is not blindly choosing ${\displaystyle i}$. That is, if ${\displaystyle S_{0}}$ encodes a false value, ${\displaystyle S_{1}}$ encodes a true value and the receiver wants to get the encoded true value, the receiver chooses ${\displaystyle i=1}$.

The oblivious transfer can be built using asymmetric cryptography like the RSA cryptosystem.

Operator ${\displaystyle \parallel }$ is string concatenation. Operator ${\displaystyle \oplus }$ is bit-wise XOR. k is a security parameter and the length of keys. It should be greater than 80 and is usually set at 128.

The Boolean circuit for small functions can be generated by hand. It is conventional to make the circuit out of 2-input XOR and AND gates. It is important that the generated circuit has the minimum number of AND gates (see Free XOR optimization). There are methods that generate the optimized circuit in term of number of AND gates using logic synthesis technique.[5] The circuit for the Millionaires' Problem is a digital comparator circuit (which is a chain of full adders working as a subtractor and outputing the carry flag). A full adder circuit can be implemented using only one AND gate and some XOR gates. This means the total number of AND gates for the circuit of the Millionaires' Problem is equal to the bit-width of the inputs.

Wires and their labels at an AND gate

Construction of the truth table of an AND gate

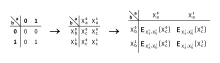
Alice (garbler) encrypts the Boolean circuit in this step to obtain a garbled circuit. Alice assigns two randomly generated strings called labels to each wire in the circuit: one for Boolean semantic 0 and one for 1. (The label is k-bit long where k the security parameter and is usually set to 128.) Next, she goes to all the gates in the circuit and replaces 0 and 1 in the truth tables with the corresponding labels. The table below shows the truth table for an AND gate with two inputs ${\displaystyle w^{a},w^{b}}$ and output ${\displaystyle w^{c}}$:

Alice replaced 0 and 1 with the corresponding labels:

a	b	c
${\displaystyle X_{0}^{a}}$	${\displaystyle X_{0}^{b}}$	${\displaystyle X_{0}^{c}}$
${\displaystyle X_{0}^{a}}$	${\displaystyle X_{1}^{b}}$	${\displaystyle X_{0}^{c}}$
${\displaystyle X_{1}^{a}}$	${\displaystyle X_{0}^{b}}$	${\displaystyle X_{0}^{c}}$
${\displaystyle X_{1}^{a}}$	${\displaystyle X_{1}^{b}}$	${\displaystyle X_{1}^{c}}$

She then encrypts the output entry of the truth table with the corresponding two input labels. The encrypted table is called garbled table. This is done such that one can decrypt the garbled table only if he has the correct two input labels. In the table below, ${\displaystyle Enc_{k}(X)}$ is a double-key symmetric encryption in which k is the secret key and X is the value to be encrypted (see Fixed-Key Blockcipher).

Garbled Table
${\displaystyle Enc_{X_{0}^{a},X_{0}^{b}}(X_{0}^{c})}$
${\displaystyle Enc_{X_{0}^{a},X_{1}^{b}}(X_{0}^{c})}$
${\displaystyle Enc_{X_{1}^{a},X_{0}^{b}}(X_{0}^{c})}$
${\displaystyle Enc_{X_{1}^{a},X_{1}^{b}}(X_{1}^{c})}$

After this, Alice randomly permutes the table such that the output value cannot be determined from the row. The protocol's name, garbled, is derived from this random permutation.

Alice sends the computed garbled tables for all gates in the circuit to Bob. Bob needs input labels to open the garbled tables. Thus, Alice chooses the labels corresponding to her input ${\displaystyle a}$ and sends them to Bob. For example, if Alice's input is ${\displaystyle \mathbf {a} =a_{4}a_{3}a_{2}a_{1}a_{0}=01101}$, then she sends ${\displaystyle X_{0}^{a_{4}}}$, ${\displaystyle X_{1}^{a_{3}}}$, ${\displaystyle X_{1}^{a_{2}}}$, ${\displaystyle X_{0}^{a_{1}}}$, and ${\displaystyle X_{1}^{a_{0}}}$ to Bob. Bob will not learn anything about Alice's input, ${\displaystyle \mathbf {a} }$, since the labels are randomly generated by Alice and they look like random strings to Bob.

Bob needs the labels corresponding to his input as well. He receives his labels through oblivious transfers for each bit of his input. For example, if Bob's input is ${\displaystyle \mathbf {b} =b_{4}b_{3}b_{2}b_{1}b_{0}=10100}$, Bob first asks for ${\displaystyle b_{0}=0}$ between Alice's labels ${\displaystyle X_{0}^{b_{0}}}$ and ${\displaystyle X_{1}^{b_{0}}}$. Through a 1-out-of-2 oblivious transfer, he receives ${\displaystyle X_{0}^{b_{0}}}$ and so on. After the oblivious transfers, Alice will not learn anything about Bob's input and Bob will not learn anything about the other labels.

After the data transfer, Bob has the garbled tables and the input labels. He goes through all gates one by one and tries to decrypt the rows in their garbled tables. He is able to open one row for each table and retrieve the corresponding output label: ${\displaystyle X^{c}=Dec_{X^{a},X^{b}}(garbled\_table[i])}$, where ${\displaystyle 0\leq i\leq 3}$. He continues the evaluation until he reaches to the output labels.

After the evaluation, Bob obtains the output label, ${\displaystyle X^{c}}$, and Alice knows its mapping to Boolean value since she has both labels: ${\displaystyle X_{0}^{c}}$ and ${\displaystyle X_{1}^{c}}$. Either Alice can share her information to Bob or Bob can reveal the output to Alice such that one or both of them learn the output.

In this optimization, Alice generates a random bit, ${\displaystyle s}$, called select bit for each wire ${\displaystyle w^{a}}$. She then sets the first bit of label 0, ${\displaystyle X_{0}^{a}}$ to ${\displaystyle s}$ and the first bit of label 1, ${\displaystyle X_{1}^{a}}$, to ${\displaystyle {\bar {s}}}$ (NOT of ${\displaystyle s}$). She then, instead of randomly permuting, sorts the garbled table according to the inputs select bit. This way, Bob does not need to test all four rows of the table to find the correct one, since he has the input labels and can find the correct row and decrypt it with one attempt. This reduces the evaluation load by 4 times. It also does not reveal anything about the output value because the select bits are randomly generated.[6]

This optimization reduces the size of garbled tables from 4 rows to 3 rows. Here, instead of generating a label for the output wire of a gate randomly, Alice generates it using a function of the input labels. She generates the output labels such that the first entry of the garbled table becomes all 0 and no longer needs to be sent:[7]

${\displaystyle {\begin{aligned}&Enc_{X_{0}^{a},X_{0}^{b}}(X_{0}^{c})=0\\&X_{0}^{c}=Dec_{X_{0}^{a},X_{0}^{b}}(0).\end{aligned}}}$

In this optimization, Alice generates a global random (k-1)-bit value ${\displaystyle R}$ which is kept secret. During the garbling of the input gates ${\displaystyle w^{a}}$ and ${\displaystyle w^{b}}$, she only generates the labels ${\displaystyle (X_{0}^{a},X_{0}^{b})}$ and computes the other labels as ${\displaystyle X_{1}^{a}=X_{0}^{a}\oplus (R\parallel 1)}$ and ${\displaystyle X_{1}^{b}=X_{0}^{b}\oplus (R\parallel 1)}$. Using these values, the label of an XOR gate's output wire ${\displaystyle w^{c}}$ with input wires ${\displaystyle w^{a}}$, ${\displaystyle w^{b}}$ is set to ${\displaystyle X^{c}=X^{a}\oplus X^{b}}$. The proof of security for this optimization is given in the Free-XOR paper.[8]

Free XOR optimization implies an important point that the amount of data transfer (communication) and number of encryption and decryption (computation) of the garbled circuit protocol relies only on the number of AND gates in the Boolean circuit not the XOR gates. Thus, between two Boolean circuits representing the same function, the one with the smaller number of AND gates is preferred.

This method allows to efficiently garble and evaluate AND gates using fixed-key AES, instead of costly cryptographic hash function like SHA-2. In this garbling scheme which is compatible with the Free XOR and Row Reduction techniques, the output key ${\displaystyle X^{c}}$ is encrypted with the input token ${\displaystyle X^{a}}$ and ${\displaystyle X^{b}}$ using the encryption function ${\displaystyle Enc(X^{a},X^{b},T,X^{c})=\pi (K)\oplus K\oplus X^{c}}$, where ${\displaystyle K=2X^{a}\oplus 4X^{b}\oplus T}$, ${\displaystyle \pi }$ is a fixed-key block cipher (e.g., instantiated with AES), and ${\displaystyle T}$ is a unique-per-gate number (e.g., gate identifier) called tweak.[9]

This optimization reduce the size of garbled table for AND gates from 3 row in Row Reduction to 2 rows. It is shown that this is the theoretical minimum for the number of rows in the garbled table, for a certain class of garbling techniques.[10]