Hoffman nucleation theory
Hoffman nucleation theory is a theory developed by John D. Hoffman and coworkers in the 1970s and 80s that attempts to describe the crystallization of a polymer in terms of the kinetics and thermodynamics of polymer surface nucleation.[1] The theory introduces a model where a surface of completely crystalline polymer is created and introduces surface energy parameters to describe the process. Hoffman nucleation theory is more of a starting point for polymer crystallization theory and is better known for its fundamental roles in the Hoffman–Weeks lamellar thickening and Lauritzen–Hoffman growth theory.
Polymer morphology
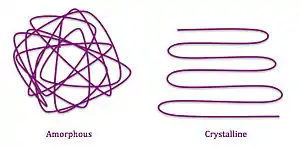
Polymers contain different morphologies on the molecular level which give rise to their macro properties. Long range disorder in the polymer chain is representative of amorphous solids, and the chain segments are considered amorphous. Long range polymer order is similar to crystalline material, and chain segments are considered crystalline.
The thermal characteristics of polymers are fundamentally different from those of most solid materials. Solid materials typically have one melting point, the Tm, above which the material loses internal molecular ordering and becomes a liquid. Polymers have both a melting temperature Tm and a glass transition temperature Tg. Above the Tm, the polymer chains lose their molecular ordering and exhibit reptation, or mobility. Below the Tm, but still above the Tg, the polymer chains lose some of their long-range mobility and can form either crystalline or amorphous regions. In this temperature range, as the temperature decreases, amorphous regions can transition into crystalline regions, causing the bulk material to become more crystalline over all. Below the Tg, molecular motion is stopped and the polymer chains are essentially frozen in place. In this temperature range, amorphous regions can no longer transition into crystalline regions, and the polymer as a whole has reached its maximum crystallinity.
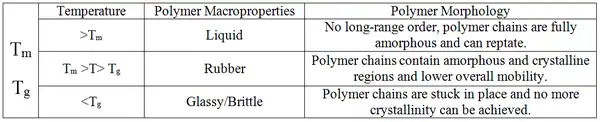
Hoffman nucleation theory addresses the amorphous to crystalline polymer transition, and this transition can only occur in the temperature range between the Tm and Tg. The transition from an amorphous to a crystalline single polymer chain is related to the random thermal energy required to align and fold sections of the chain to form ordered regions titled lamellae, which are a subset of even bigger structures called spherulites. The crystallization of polymers can be brought about by several different methods, and is a complex topic in itself.
Nucleation
Nucleation is the formation and growth of a new phase with or without the presence of external surface. The presence of this surface results in heterogeneous nucleation whereas in its absence homogeneous nucleation occurs. Heterogeneous nucleation occurs in cases where there are pre-existing nuclei present, such as tiny dust particles suspended in a liquid or gas or reacting with a glass surface containing SiO2. For the process of Hoffman nucleation and its progression to Lauritzen–Hoffman growth theory, homogeneous nucleation is the main focus. Homogeneous nucleation occurs where no such contaminants are present and is less commonly seen. Homogeneous nucleation begins with small clusters of molecules forming from one phase to the next. As the clusters grow, they aggregate through the condensation of other molecules. The size continues to increase and ultimately form macroscopic droplets (or bubbles depending on the system).
Nucleation is often described mathematically through the change in Gibbs free energy of n moles of vapor at vapor pressure P that condenses into a drop. Also the nucleation barrier, in polymer crystallization, consists of both enthalpic and entropic components that must be over come. This barrier consists of selection processes taking place in different length and time scales which relates to the multiple regimes later on.[2] This barrier is the free energy required to overcome in order to form nuclei. It is the formation of the nuclei from the bulk to a surface that is the interfacial free energy. The interfacial free energy is always a positive term and acts to destabilize the nucleus allowing the continuation of the growing polymer chain. The nucleation continues as a favorable reaction.
Thermodynamics of polymer crystallization
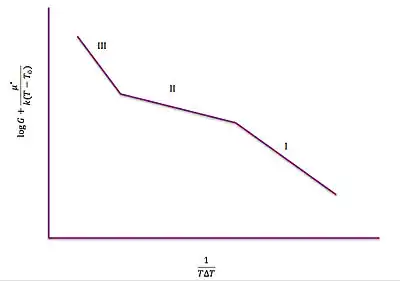
The Lauritzen–Hoffman plot (right) models the three different regimes when (logG) + U*/k(T-T0) is plotted against (TΔT)−1.[3] It can be used to describe the rate at which secondary nucleation competes with lateral addition at the growth front among the different temperatures. This theory can be used to help understand the preferences of nucleation and growth based on the polymer's properties including its standard melting temperature.
Lamellar thickening (Hoffman–Weeks plot)
For many polymers, the change between the initial lamellar thickness at Tc is roughly the same as at Tm and can thus be modeled by the Gibbs–Thomson equation fairly well. However, since it implies that the lamellar thickness over the given supercooling range (Tm–Tc) is unchanged, and many homogeneous nucleation of polymers implies a change of thickness at the growth front, Hoffman and Weeks pursued a more accurate representation.[4] In this regard, the Hoffman-Weeks plot was created and can be modeled through the equation
where β is representative of a thickening factor given by L = L0 β and Tcand Tm are the crystallization and melting temperatures, respectively.
Applying this experimentally for a constant β allows for the determination of the equilibrium melting temperature, Tm° at the intersection of Tcand Tm.[3]
Kinetics of polymer crystallization
The crystallization process of polymers does not always obey simple chemical rate equations. Polymers can crystallize through a variety of different regimes and unlike simple molecules, the polymer crystal lamellae have two very different surfaces. The two most prominent theories in polymer crystallization kinetics are the Avrami equation and Lauritzen–Hoffman growth theory.[5]
Lauritzen–Hoffman growth theory
The Lauritzen–Hoffman growth theory breaks the kinetics of polymer crystallization into ultimately two rates. The model breaks down into the addition of monomers onto a growing surface. This initial step is generally associated with the nucleation of the polymer. From there, the kinetics become the rate which the polymer grows on the surface, or the lateral growth rate, in comparison with the growth rate onto the polymer extending the chain, the secondary nucleation rate. These two rates can result in three situations.[6]
Three regimes of crystallization kinetics
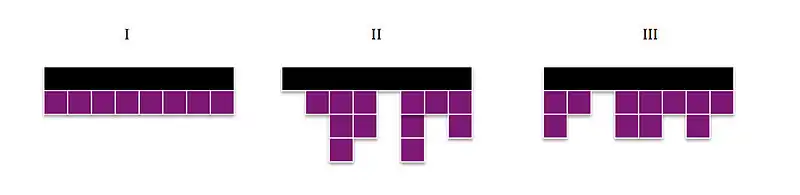
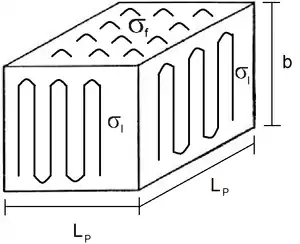
For Regime I, the growth rate on the front laterally, referred to as g, is the rate-determining step (RDS) and exceeds the secondary nucleation rate, i. In this instance of g >> i, monolayers are formed one at a time so that if the substrate has a length of Lp and thickness, b, the overall linear growth can be described through the equation
and the rate of nucleation in specific can further be described by
with Kg equal to
where
- σl is the lateral/lamellae surface free energy per unit area
- σf is the fold surface free energy per unit area
- Tm0 is the equilibrium melting temperature
- k is equal to Boltzmann constant
- Δh is equal to the change of enthalpy of fusion (or latent heat of fusion) per repeat unit at the standard temperature[3]
This shows that in Region I, lateral nucleation along the front successfully dominates at temperatures close to the melting temperature, however at more extreme temperatures other forces such as diffusion can impact nucleation rates.
In Regime II, the lateral growth rate is either comparable or smaller than the nucleation rate g ≤ i, which causes secondary (or more) layers to form before the initial layer has been covered. This allows the linear growth rate to be modeled by
Using the assumption that g and i are independent of time, the rate at which new layers are formed can be approximated and the rate of nucleation in regime II can be expressed as
with Kg' equal to about 1/2 of the Kg from Regime I,
Lastly, Regime III in the L-H model depicts the scenario where lateral growth is inconsequential to the overall rate, since the nucleation of multiple sites causes i >> g. This means that the growth rate can be modeled by the same equation as Regime I,
where GIII° is the prefactor for Regime III and can be experimentally determined through applying the Lauritzen–Hoffman Plot.[7]
Polyethylene crystallization kinetics
A reza's crystallization depends on the time it takes for layers of its chains to fold and orient themselves in the same direction. This time increases with a molecule's weight and branching.[8] The table below shows that the growth rate is higher for Sclair 14B.1 than Sclair 2907 (20%), where 2907 is less highly branched than 14B.1.[8] Here Gc is the crystal growth rate, or how quickly it orders itself depending on the layers, and t is the time it takes to order.
| Polymer | Growth Temp (°C) | Gc (μm*min−1) | t (ms) |
|---|---|---|---|
| Sclair 2907 (20%) | 119 | 3.5-6.8 | 4.4-8.6 |
| Sclair 14B.1 | 119 | ~0.2 | ~150 |
Further testing and applications
Many additional tests have since been run to apply and compare Hoffman's principles to reality. Among the experiments done, some of the more notable secondary nucleation tests are briefly explained in the table below.
| Secondary nucleation testing | Experimental results observed |
|---|---|
| Potassium chloride (KCl) | Secondary nuclei form at a rate proportional to the degree of supercooling (above certain levels of agitation) and achieve the same amount of nucleation regardless of the shape of the parent crystal. This is due to the substantially greater effect of secondary nucleation over primary nucleation of the original crystal. This was proven through both temperature and shape dependent nuclei stimulated growth experiments to confirm that in cases of secondary nucleation only the degree and temperature of supercooling change the nucleation rate, whereas the parent crystal only serves to act as a catalytic initiator of the process.[9] |
| Isotactic poly (vinylcyclohexane) (PVCH) | PVCH crystals were experimentally shown to increase their spread and lateral growth at high temperatures indicating that although they were feasibly unable to reach Regime III temperatures, extrapolations and hypotheses from the experiment point to confirmation of the expected behavior in each of the three regimes. Experiments concluded that additional growth mechanisms such as crystal twinning and twin boundary interactions can alter the traditional LH theory, but further research is needed to model each individual influence.[10] |
| Zinc oxide (ZnO) | Zinc oxide crystals were proven to undergo secondary nucleation under an odd mixture of conditions including the addition of a diamine as well as surface etching. Overall, testing has shown that the morphology of the secondary crystals can fluctuate greatly depending on the amount of diamine added, due to its ability to deplete the substrate and hinder the growth prematurely.[11] |
References
- N. B. Hannay (1976). "7". Treatise on Solid State Chemistry. 3. Plenum Press. doi:10.1002/pol.1977.130150310.
- Cheng, Stephen; Lotz, Bernard (2005). "Enthalpic and entropic origins of nucleation barriers during polymer crystallization: the Hoffman–Lauritzen theory and beyond". Polymer. 46 (20): 8662–8681. doi:10.1016/j.polymer.2005.03.125.
- Muthukumar, M (2004). "Nucleation in Polymer Crystallization". Advances in Chemical Physics. 128. ISBN 0-471-44528-2.
- Marand, Herve; Xu, Jiannong; Srinivas, Srivatsan (1998). "Determination of the Equilibrium Melting Temperature of Polymer Crystals: Linear and Nonlinear Hoffman-Weeks Extrapolations". Macromolecules. 31 (23): 8219–8229. Bibcode:1998MaMol..31.8219M. doi:10.1021/ma980747y.
- Paul C. Painter, Michael M. Coleman (1997). "8". Fundamentals of Polymer Science An Introductory Text, Second Edition. CRC Press.
- Snyder, Chad R.; Marand, Herve; Mansfield, Marc L. (1996). "Lateral Substrate Completion Rate in the Lauritzen-Hoffman Secondary Surface Nucleation Theory: Nature of the Friction Coefficient". Macromolecules. 29 (23): 7508–7513. Bibcode:1996MaMol..29.7508S. doi:10.1021/ma960589f.
- Snyder, Chad R.; Marand, Herve (1997). "Effect of Chain Transport in the Secondary Surface Nucleation Based Flux Theory and in the Lauritzen-Hoffman Crystal Growth Rate Formalism". Macromolecules. 30 (9): 2759–2766. Bibcode:1997MaMol..30.2759S. doi:10.1021/ma961633u.
- el Maaty, M.I. Abo; Bassett, D. C. (4 October 2006). "On the time for fold surfaces to order during the crystallization of polyethylene from the melt and its dependence on molecular parameters". Polymer. 47 (21): 7469–7476. doi:10.1016/j.polymer.2006.08.015.
- Melia, T.P.; Moffitt, W.P. (1964). "Secondary Nucleation from Aqueous Solution". Industrial & Engineering Chemistry Fundamentals. 3 (4): 314–317. doi:10.1021/i160012a006.
- Alcazar, Daniel; Thierry, Annette; Schultz, Patrick; Kawaguchi, Akiyoshi; Cheng, Stephen Z. D.; Lotz, Bernard (2006). "Determination of the Extent of Lateral Spread and Density of Secondary Nucleation in Polymer Single Crystal Growth". Macromolecules. 39 (26): 9120–9131. Bibcode:2006MaMol..39.9120A. doi:10.1021/ma061697x.
- Sounart, Thomas L.; Liu, Jun; Voigt, James A.; Huo, Mae; Spoerke, Erik D.; McKenzie, Bonnie (2007). "Secondary Nucleation and Growth of ZnO". J. Am. Chem. Soc. 129 (51): 15786–15793. doi:10.1021/ja071209g.