Interval order
In mathematics, especially order theory, the interval order for a collection of intervals on the real line is the partial order corresponding to their left-to-right precedence relation—one interval, I1, being considered less than another, I2, if I1 is completely to the left of I2. More formally, a poset is an interval order if and only if there exists a bijection from to a set of real intervals, so , such that for any we have in exactly when . Such posets may be equivalently characterized as those with no induced subposet isomorphic to the pair of two-element chains, in other words as the -free posets .[1]
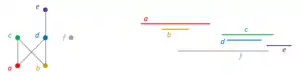
.svg.png.webp)
The subclass of interval orders obtained by restricting the intervals to those of unit length, so they all have the form , is precisely the semiorders.
The complement of the comparability graph of an interval order (, ≤) is the interval graph .
Interval orders should not be confused with the interval-containment orders, which are the inclusion orders on intervals on the real line (equivalently, the orders of dimension ≤ 2).
Interval orders and dimension
| Unsolved problem in mathematics: What is the complexity of determining the order dimension of an interval order? (more unsolved problems in mathematics) |
An important parameter of partial orders is order dimension: the dimension of a partial order is the least number of linear orders whose intersection is . For interval orders, dimension can be arbitrarily large. And while the problem of determining the dimension of general partial orders is known to be NP-hard, determining the dimension of an interval order remains a problem of unknown computational complexity.[2]
A related parameter is interval dimension, which is defined analogously, but in terms of interval orders instead of linear orders. Thus the interval dimension of a partially ordered set is the least integer for which there exist interval orders on with exactly when and . The interval dimension of an order is never greater than its order dimension,.[3]
Combinatorics
In addition to being isomorphic to -free posets, unlabeled interval orders on are also in bijection with a subset of fixed-point-free involutions on ordered sets with cardinality .[4] These are the involutions with no so-called left- or right-neighbor nestings where, for any involution on , a left nesting is an such that and a right nesting is an such that .
Such involutions, according to semi-length, have ordinary generating function [5]
The coefficient of in the expansion of gives the number of unlabeled interval orders of size . The sequence of these numbers (sequence A022493 in the OEIS) begins
- 1, 2, 5, 15, 53, 217, 1014, 5335, 31240, 201608, 1422074, 10886503, 89903100, 796713190, 7541889195, 75955177642, …
Notes
References
- Bousquet-Mélou, Mireille; Claesson, Anders; Dukes, Mark; Kitaev, Sergey (2010), "(2+2) free posets, ascent sequences and pattern avoiding permutations", Journal of Combinatorial Theory, Series A, 117 (7): 884–909, arXiv:0806.0666, doi:10.1016/j.jcta.2009.12.007, MR 2652101, S2CID 8677150.
- Felsner, S. (1992), Interval Orders: Combinatorial Structure and Algorithms (PDF), Ph.D. dissertation, Technical University of Berlin.
- Felsner, S.; Habib, M.; Möhring, R. H. (1994), "On the interplay between interval dimension and dimension" (PDF), SIAM Journal on Discrete Mathematics, 7 (1): 32–40, doi:10.1137/S089548019121885X, MR 1259007.
- Fishburn, Peter C. (1970), "Intransitive indifference with unequal indifference intervals", Journal of Mathematical Psychology, 7 (1): 144–149, doi:10.1016/0022-2496(70)90062-3, MR 0253942.
- Zagier, Don (2001), "Vassiliev invariants and a strange identity related to the Dedekind eta-function", Topology, 40 (5): 945–960, doi:10.1016/s0040-9383(00)00005-7, MR 1860536.
Further reading
- Fishburn, Peter (1985), Interval Orders and Interval Graphs: A Study of Partially Ordered Sets, John Wiley
