Involution (mathematics)
In mathematics, an involution, or an involutory function, is a function f that is its own inverse,
- f(f(x)) = x
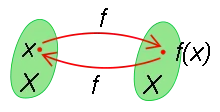
for all x in the domain of f.[1] Equivalently, applying f twice produces the original value.
The term anti-involution refers to involutions based on antihomomorphisms (see § Quaternion algebra, groups, semigroups below)
- f(xy) = f(y) f(x)
such that
- xy = f(f(xy)) = f( f(y) f(x) ) = f(f(x)) f(f(y)) = xy.
General properties
Any involution is a bijection.
The identity map is a trivial example of an involution. Common examples in mathematics of nontrivial involutions include multiplication by −1 in arithmetic, the taking of reciprocals, complementation in set theory and complex conjugation. Other examples include circle inversion, rotation by a half-turn, and reciprocal ciphers such as the ROT13 transformation and the Beaufort polyalphabetic cipher.
The number of involutions, including the identity involution, on a set with n = 0, 1, 2, ... elements is given by a recurrence relation found by Heinrich August Rothe in 1800:
- and for
The first few terms of this sequence are 1, 1, 2, 4, 10, 26, 76, 232 (sequence A000085 in the OEIS); these numbers are called the telephone numbers, and they also count the number of Young tableaux with a given number of cells.[2] The composition g ∘ f of two involutions f and g is an involution if and only if they commute: g ∘ f = f ∘ g.[3]
Every involution on an odd number of elements has at least one fixed point. More generally, for an involution on a finite set of elements, the number of elements and the number of fixed points have the same parity.[4]
Involution throughout the fields of mathematics
Pre-calculus
Basic examples of involutions are the functions:
- , or , as well as their composition
These are not the only pre-calculus involutions. Another one within the positive reals is:
The graph of an involution (on the real numbers) is line-symmetric over the line . This is due to the fact that the inverse of any general function will be its reflection over the 45° line . This can be seen by "swapping" with . If, in particular, the function is an involution, then it will serve as its own reflection.
Other elementary involutions are useful in solving functional equations.
Euclidean geometry
A simple example of an involution of the three-dimensional Euclidean space is reflection through a plane. Performing a reflection twice brings a point back to its original coordinates.
Another involution is reflection through the origin; not a reflection in the above sense, and so, a distinct example.
These transformations are examples of affine involutions.
Projective geometry
An involution is a projectivity of period 2, that is, a projectivity that interchanges pairs of points.[5]:24
- Any projectivity that interchanges two points is an involution.
- The three pairs of opposite sides of a complete quadrangle meet any line (not through a vertex) in three pairs of an involution. This theorem has been called Desargues's Involution Theorem.[6] Its origins can be seen in Lemma IV of the lemmas to the Porisms of Euclid in Volume VII of the Collection of Pappus of Alexandria.[7]
- If an involution has one fixed point, it has another, and consists of the correspondence between harmonic conjugates with respect to these two points. In this instance the involution is termed "hyperbolic", while if there are no fixed points it is "elliptic". In the context of projectivities, fixed points are called double points.[5]:53
Another type of involution occurring in projective geometry is a polarity which is a correlation of period 2. [8]
Linear algebra
In linear algebra, an involution is a linear operator T on a vector space, such that . Except for in characteristic 2, such operators are diagonalizable for a given basis with just 1s and −1s on the diagonal of the corresponding matrix. If the operator is orthogonal (an orthogonal involution), it is orthonormally diagonalizable.
For example, suppose that a basis for a vector space V is chosen, and that e1 and e2 are basis elements. There exists a linear transformation f which sends e1 to e2, and sends e2 to e1, and which is the identity on all other basis vectors. It can be checked that f(f(x)) = x for all x in V. That is, f is an involution of V.
For a specific basis, any linear operator can be represented by a matrix T. Every matrix has a transpose, obtained by swapping rows for columns. This transposition is an involution on the set of matrices.
The definition of involution extends readily to modules. Given a module M over a ring R, an R endomorphism f of M is called an involution if f 2 is the identity homomorphism on M.
Involutions are related to idempotents; if 2 is invertible then they correspond in a one-to-one manner.
Quaternion algebra, groups, semigroups
In a quaternion algebra, an (anti-)involution is defined by the following axioms: if we consider a transformation then it is an involution if
- (it is its own inverse)
- and (it is linear)
An anti-involution does not obey the last axiom but instead
This former law is sometimes called antidistributive. It also appears in groups as (xy)−1 = y−1x−1. Taken as an axiom, it leads to the notion of semigroup with involution, of which there are natural examples that are not groups, for example square matrix multiplication (i.e. the full linear monoid) with transpose as the involution.
Ring theory
In ring theory, the word involution is customarily taken to mean an antihomomorphism that is its own inverse function. Examples of involutions in common rings:
- complex conjugation on the complex plane
- multiplication by j in the split-complex numbers
- taking the transpose in a matrix ring.
Group theory
In group theory, an element of a group is an involution if it has order 2; i.e. an involution is an element a such that a ≠ e and a2 = e, where e is the identity element.[9]
Originally, this definition agreed with the first definition above, since members of groups were always bijections from a set into itself; i.e., group was taken to mean permutation group. By the end of the 19th century, group was defined more broadly, and accordingly so was involution.
A permutation is an involution precisely if it can be written as a product of one or more non-overlapping transpositions.
The involutions of a group have a large impact on the group's structure. The study of involutions was instrumental in the classification of finite simple groups.
An element x of a group G is called strongly real if there is an involution t with xt = x−1 (where xt = t−1⋅x⋅t).
Coxeter groups are groups generated by involutions with the relations determined only by relations given for pairs of the generating involutions. Coxeter groups can be used, among other things, to describe the possible regular polyhedra and their generalizations to higher dimensions.
Mathematical logic
The operation of complement in Boolean algebras is an involution. Accordingly, negation in classical logic satisfies the law of double negation: ¬¬A is equivalent to A.
Generally in non-classical logics, negation that satisfies the law of double negation is called involutive. In algebraic semantics, such a negation is realized as an involution on the algebra of truth values. Examples of logics which have involutive negation are Kleene and Bochvar three-valued logics, Łukasiewicz many-valued logic, fuzzy logic IMTL, etc. Involutive negation is sometimes added as an additional connective to logics with non-involutive negation; this is usual, for example, in t-norm fuzzy logics.
The involutiveness of negation is an important characterization property for logics and the corresponding varieties of algebras. For instance, involutive negation characterizes Boolean algebras among Heyting algebras. Correspondingly, classical Boolean logic arises by adding the law of double negation to intuitionistic logic. The same relationship holds also between MV-algebras and BL-algebras (and so correspondingly between Łukasiewicz logic and fuzzy logic BL), IMTL and MTL, and other pairs of important varieties of algebras (resp. corresponding logics).
In the study of binary relations, every relation has a converse relation. Since the converse of the converse is the original relation, the conversion operation is an involution on the category of relations. Binary relations are ordered through inclusion. While this ordering is reversed with the complementation involution, it is preserved under conversion.
Computer science
The XOR bitwise operation with a given value for one parameter is an involution. XOR masks were once used to draw graphics on images in such a way that drawing them twice on the background reverts the background to its original state. The NOT bitwise operation is also an involution, and is a special case of the XOR operation where one parameter has all bits set to 1.
Another example is a bit mask and shift function operating on color values stored as integers, say in the form RGB, that swaps R and B, resulting in the form BGR. f(f(RGB))=RGB, f(f(BGR))=BGR.
The RC4 cryptographic cipher is an involution, as encryption and decryption operations use the same function.
Practically all mechanical cipher machines implement a reciprocal cipher, an involution on each typed-in letter. Instead of designing two kinds of machines, one for encrypting and one for decrypting, all the machines can be identical and can be set up (keyed) the same way.[10]
See also
References
- Russell, Bertrand (1903), Principles of mathematics (2nd ed.), W. W. Norton & Company, Inc, p. 426, ISBN 9781440054167
- Knuth, Donald E. (1973), The Art of Computer Programming, Volume 3: Sorting and Searching, Reading, Mass.: Addison-Wesley, pp. 48, 65, MR 0445948.
- Kubrusly, Carlos S. (2011), The Elements of Operator Theory, Springer Science & Business Media, Problem 1.11(a), p. 27, ISBN 9780817649982.
- Zagier, D. (1990), "A one-sentence proof that every prime p≡ 1 (mod 4) is a sum of two squares", American Mathematical Monthly, 97 (2): 144, doi:10.2307/2323918, JSTOR 2323918, MR 1041893.
- A.G. Pickford (1909) Elementary Projective Geometry, Cambridge University Press via Internet Archive
- J. V. Field and J. J. Gray (1987) The Geometrical Work of Girard Desargues, (New York: Springer), p. 54
- Ivor Thomas (editor) (1980) Selections Illustrating the History of Greek Mathematics, Volume II, number 362 in the Loeb Classical Library (Cambridge and London: Harvard and Heinemann), pp. 610–3
- H. S. M. Coxeter (1969) Introduction to Geometry, pp 244–8, John Wiley & Sons
- John S. Rose. "A Course on Group Theory". p. 10, section 1.13.
- Greg Goebel. "The Mechanization of Ciphers". 2018.
Further reading
- Ell, Todd A.; Sangwine, Stephen J. (2007). "Quaternion involutions and anti-involutions". Computers & Mathematics with Applications. 53 (1): 137–143. arXiv:math/0506034. doi:10.1016/j.camwa.2006.10.029. S2CID 45639619.
- Knus, Max-Albert; Merkurjev, Alexander; Rost, Markus; Tignol, Jean-Pierre (1998), The book of involutions, Colloquium Publications, 44, With a preface by J. Tits, Providence, RI: American Mathematical Society, ISBN 0-8218-0904-0, Zbl 0955.16001
- "Involution", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
