Inverted snub dodecadodecahedron
In geometry, the inverted snub dodecadodecahedron (or vertisnub dodecadodecahedron) is a nonconvex uniform polyhedron, indexed as U60.[1] It is given a Schläfli symbol sr{5/3,5}.
| Inverted snub dodecadodecahedron | |
|---|---|
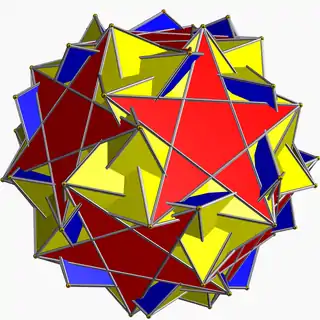 | |
| Type | Uniform star polyhedron |
| Elements | F = 84, E = 150 V = 60 (χ = −6) |
| Faces by sides | 60{3}+12{5}+12{5/2} |
| Wythoff symbol | | 5/3 2 5 |
| Symmetry group | I, [5,3]+, 532 |
| Index references | U60, C76, W114 |
| Dual polyhedron | Medial inverted pentagonal hexecontahedron |
| Vertex figure | 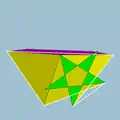 3.3.5.3.5/3 |
| Bowers acronym | Isdid |

Cartesian coordinates
Cartesian coordinates for the vertices of an inverted snub dodecadodecahedron are all the even permutations of
- (±2α, ±2, ±2β),
- (±(α+β/τ+τ), ±(-ατ+β+1/τ), ±(α/τ+βτ-1)),
- (±(-α/τ+βτ+1), ±(-α+β/τ-τ), ±(ατ+β-1/τ)),
- (±(-α/τ+βτ-1), ±(α-β/τ-τ), ±(ατ+β+1/τ)) and
- (±(α+β/τ-τ), ±(ατ-β+1/τ), ±(α/τ+βτ+1)),
with an even number of plus signs, where
- β = (α2/τ+τ)/(ατ−1/τ),
where τ = (1+√5)/2 is the golden mean and α is the negative real root of τα4−α3+2α2−α−1/τ, or approximately −0.3352090. Taking the odd permutations of the above coordinates with an odd number of plus signs gives another form, the enantiomorph of the other one.
Related polyhedra
Medial inverted pentagonal hexecontahedron
| Medial inverted pentagonal hexecontahedron | |
|---|---|
 | |
| Type | Star polyhedron |
| Face |  |
| Elements | F = 60, E = 150 V = 84 (χ = −6) |
| Symmetry group | I, [5,3]+, 532 |
| Index references | DU60 |
| dual polyhedron | Inverted snub dodecadodecahedron |

The medial inverted pentagonal hexecontahedron (or midly petaloid ditriacontahedron) is a nonconvex isohedral polyhedron. It is the dual of the uniform inverted snub dodecadodecahedron. Its faces are irregular nonconvex pentagons, with one very acute angle.
Proportions
Denote the golden ratio by , and let be the largest (least negative) real zero of the polynomial . Then each face has three equal angles of , one of and one of . Each face has one medium length edge, two short and two long ones. If the medium length is , then the short edges have length
- ,
and the long edges have length
- .
The dihedral angle equals . The other real zero of the polynomial plays a similar role for the medial pentagonal hexecontahedron.
References
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 0730208 p. 124
- Roman, Maeder. "60: inverted snub dodecadodecahedron". MathConsult.
External links
- Weisstein, Eric W. "Medial inverted pentagonal hexecontahedron". MathWorld.
- Weisstein, Eric W. "Inverted snub dodecadodecahedron". MathWorld.