Khatri–Rao product
In mathematics, the Khatri–Rao product is defined as[1][2]
in which the ij-th block is the mipi × njqj sized Kronecker product of the corresponding blocks of A and B, assuming the number of row and column partitions of both matrices is equal. The size of the product is then (Σi mipi) × (Σj njqj).
For example, if A and B both are 2 × 2 partitioned matrices e.g.:
we obtain:
This is a submatrix of the Tracy–Singh product of the two matrices (each partition in this example is a partition in a corner of the Tracy–Singh product) and also may be called the block Kronecker product.
Column-wise Khatri–Rao product
A column-wise Kronecker product of two matrices may also be called the Khatri–Rao product. This product assumes the partitions of the matrices are their columns. In this case m1 = m, p1 = p, n = q and for each j: nj = pj = 1. The resulting product is a mp × n matrix of which each column is the Kronecker product of the corresponding columns of A and B. Using the matrices from the previous examples with the columns partitioned:
so that:
This column-wise version of the Khatri–Rao product is useful in linear algebra approaches to data analytical processing[3] and in optimizing the solution of inverse problems dealing with a diagonal matrix.[4][5]
In 1996 the Column-wise Khatri–Rao product was proposed to estimate the Angle of arrivals (AOAs) and delays of multipath signals[6] and four coordinates of signals sources[7] at a digital antenna array.
Face-splitting product

The alternative concept of the matrix product, which uses row-wise splitting of matrices with a given quantity of rows, was proposed by V. Slyusar[8] in 1996.[7][9][10][11][12]
This matrix operation was named the "face-splitting product" of matrices[9][11] or the "transposed Khatri–Rao product". This type of operation is based on row-by-row Kronecker products of two matrices. Using the matrices from the previous examples with the rows partitioned:
the result can be obtained:[7][9][11]
Main properties
- Transpose (V. Slyusar, 1996[7][9][10]):
- ,
- Bilinearity and associativity[7][9][10]:
where A, B and C are matrices, and k is a scalar,
- ,[10]
- The mixed-product property (V. Slyusar, 1997[10]):
- ,
- ,
- ,[14]
- ,[10]
- ,[7]
- ,[14]
- [11][13],
Similarly:
, - [10],
, where and are vectors, - ,[15] ,
- ,[16]
where and are vectors (it is a combine of properties 3 an 8),
Similarly: - ,
where is vector convolution and is the Fourier transform matrix (this result is an evolving of count sketch properties[17] ), - [18],
where is matrix, is matrix, is a vector of 1's of length , and is a vector of 1's of length
or
,[19] where is matrix, means element by element multiplication and is a vector of 1's of length .
, where denotes the penetrating face product of matrices[11].
Similarly:
, where is matrix, is matrix,. - [10],
,[19] where is the vector consisting of the diagonal elements of , means stack the columns of a matrix on top of each other to give a vector. - [11][13].
Similarly:
, , where and are vectors
Examples[16]
Theorem[16]
- If , where are independent comprises a matrix with i.i.d. rows , such that and ,
- then with probability for any vector if the qwauntinty of rows
In particular, if the entries of are can get which matches the Johnson–Lindenstrauss lemma of when is small.
Block face-splitting product
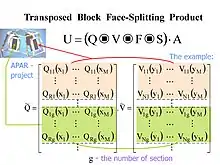
According to the definition of V. Slyusar [7][11] the block face-splitting product of two partitioned matrices with a given quantity of rows in blocks
can be written as :
- .
The transposed block face-splitting product (or Block column-wise version of the Khatri–Rao product) of two partitioned matrices with a given quantity of columns in blocks has a view:[7][11]
- .
Applications
The Face-splitting product and the Block Face-splitting product used in the tensor-matrix theory of digital antenna arrays. These operations used also in Artificial Intelligence and Machine learning systems to minimization of convolution and tensor sketch operations,[16] in a popular Natural Language Processing models, and hypergraph models of similarity,[20] Generalized linear array model in statistics[19] and two- and multidimensional P-spline approximation of data.[18]
See also
Notes
- Khatri C. G., C. R. Rao (1968). "Solutions to some functional equations and their applications to characterization of probability distributions". Sankhya. 30: 167–180. Archived from the original on 2010-10-23. Retrieved 2008-08-21.
- Zhang X; Yang Z; Cao C. (2002), "Inequalities involving Khatri–Rao products of positive semi-definite matrices", Applied Mathematics E-notes, 2: 117–124
- See e.g. H. D. Macedo and J.N. Oliveira. A linear algebra approach to OLAP. Formal Aspects of Computing, 27(2):283–307, 2015.
- Lev-Ari, Hanoch (2005-01-01). "Efficient Solution of Linear Matrix Equations with Application to Multistatic Antenna Array Processing". Communications in Information & Systems. 05 (1): 123–130. doi:10.4310/CIS.2005.v5.n1.a5. ISSN 1526-7555.
- Masiero, B.; Nascimento, V. H. (2017-05-01). "Revisiting the Kronecker Array Transform". IEEE Signal Processing Letters. 24 (5): 525–529. Bibcode:2017ISPL...24..525M. doi:10.1109/LSP.2017.2674969. ISSN 1070-9908.
- Vanderveen, M. C., Ng, B. C., Papadias, C. B., & Paulraj, A. (n.d.). Joint angle and delay estimation (JADE) for signals in multipath environments. Conference Record of The Thirtieth Asilomar Conference on Signals, Systems and Computers. – DOI:10.1109/acssc.1996.599145
- Slyusar, V. I. (December 27, 1996). "End products in matrices in radar applications" (PDF). Radioelectronics and Communications Systems.– 1998, Vol. 41; Number 3: 50–53.
- Anna Esteve, Eva Boj & Josep Fortiana (2009): "Interaction Terms in Distance-Based Regression," Communications in Statistics – Theory and Methods, 38:19, p. 3501
- Slyusar, V. I. (1997-05-20). "Analytical model of the digital antenna array on a basis of face-splitting matrix products" (PDF). Proc. ICATT-97, Kyiv: 108–109.
- Slyusar, V. I. (1997-09-15). "New operations of matrices product for applications of radars" (PDF). Proc. Direct and Inverse Problems of Electromagnetic and Acoustic Wave Theory (DIPED-97), Lviv.: 73–74.
- Slyusar, V. I. (March 13, 1998). "A Family of Face Products of Matrices and its Properties" (PDF). Cybernetics and Systems Analysis C/C of Kibernetika I Sistemnyi Analiz. 1999. 35 (3): 379–384. doi:10.1007/BF02733426.
- Slyusar, V. I. (2003). "Generalized face-products of matrices in models of digital antenna arrays with nonidentical channels" (PDF). Radioelectronics and Communications Systems. 46 (10): 9–17.
- Vadym Slyusar. New Matrix Operations for DSP (Lecture). April 1999. – DOI: 10.13140/RG.2.2.31620.76164/1
- C. Radhakrishna Rao. Estimation of Heteroscedastic Variances in Linear Models.//Journal of the American Statistical Association, Vol. 65, No. 329 (Mar., 1970), pp. 161–172
- Kasiviswanathan, Shiva Prasad, et al. «The price of privately releasing contingency tables and the spectra of random matrices with correlated rows.» Proceedings of the forty-second ACM symposium on Theory of computing. 2010.
- Thomas D. Ahle, Jakob Bæk Tejs Knudsen. Almost Optimal Tensor Sketch. Published 2019. Mathematics, Computer Science, ArXiv
- Ninh, Pham; Rasmus, Pagh (2013). Fast and scalable polynomial kernels via explicit feature maps. SIGKDD international conference on Knowledge discovery and data mining. Association for Computing Machinery. doi:10.1145/2487575.2487591.
- Eilers, Paul H.C.; Marx, Brian D. (2003). "Multivariate calibration with temperature interaction using two-dimensional penalized signal regression". Chemometrics and Intelligent Laboratory Systems. 66 (2): 159–174. doi:10.1016/S0169-7439(03)00029-7.
- Currie, I. D.; Durban, M.; Eilers, P. H. C. (2006). "Generalized linear array models with applications to multidimensional smoothing". Journal of the Royal Statistical Society. 68 (2): 259–280. doi:10.1111/j.1467-9868.2006.00543.x.
- Bryan Bischof. Higher order co-occurrence tensors for hypergraphs via face-splitting. Published 15 February, 2020, Mathematics, Computer Science, ArXiv
References
- Khatri C. G., C. R. Rao (1968). "Solutions to some functional equations and their applications to characterization of probability distributions". Sankhya. 30: 167–180. Archived from the original on 2010-10-23. Retrieved 2008-08-21.
- Zhang X; Yang Z; Cao C. (2002), "Inequalities involving Khatri–Rao products of positive semi-definite matrices", Applied Mathematics E-notes, 2: 117–124
- Matrix Algebra & Its Applications to Statistics & Econometrics./C. R. Rao with M. Bhaskara Rao. – World Scientific. – 1998. – p. 216.