Kirkwood gap

A Kirkwood gap is a gap or dip in the distribution of the semi-major axes (or equivalently of the orbital periods) of the orbits of main-belt asteroids. They correspond to the locations of orbital resonances with Jupiter.

Histogram showing the four most prominent Kirkwood gaps and a possible division into inner, middle and outer main-belt asteroids:
  inner main-belt (a < 2.5 AU)
  intermediate main-belt (2.5 AU < a < 2.82 AU)
  outer main-belt (a > 2.82 AU)
Relation between Jovian orbital resonance and the distance from the Sun in Kirkwood gaps

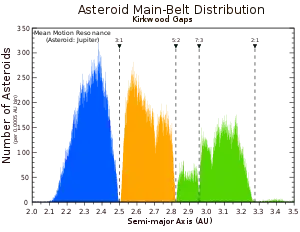
For example, there are very few asteroids with semimajor axis near 2.50 AU, period 3.95 years, which would make three orbits for each orbit of Jupiter (hence, called the 3:1 orbital resonance). Other orbital resonances correspond to orbital periods whose lengths are simple fractions of Jupiter's. The weaker resonances lead only to a depletion of asteroids, while spikes in the histogram are often due to the presence of a prominent asteroid family (see List of asteroid families).

The gaps were first noticed in 1866 by Daniel Kirkwood, who also correctly explained their origin in the orbital resonances with Jupiter while a professor at Jefferson College in Canonsburg, Pennsylvania.[1]

Most of the Kirkwood gaps are depleted, unlike the mean-motion resonances (MMR) of Neptune or Jupiter's 3:2 resonance, that retain objects captured during the giant planet migration of the Nice model. The loss of objects from the Kirkwood gaps is due to the overlapping of the ν5 and ν6 secular resonances within the mean-motion resonances. The orbital elements of the asteroids vary chaotically as a result and evolve onto planet-crossing orbits within a few million years.[2] The 2:1 MMR has a few relatively stable islands within the resonance, however. These islands are depleted due to slow diffusion onto less stable orbits. This process, which has been linked to Jupiter and Saturn being near a 5:2 resonance, may have been more rapid when Jupiter's and Saturn's orbits were closer together.[3]

More recently, a relatively small number of asteroids have been found to possess high eccentricity orbits which do lie within the Kirkwood gaps. Examples include the Alinda and Griqua groups. These orbits slowly increase their eccentricity on a timescale of tens of millions of years, and will eventually break out of the resonance due to close encounters with a major planet.

Main gaps

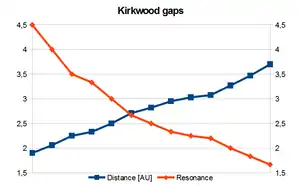
The most prominent Kirkwood gaps are located at mean orbital radii of:[4]

  • 2.06 AU (4:1 resonance)
  • 2.50 AU (3:1 resonance), home to the Alinda group of asteroids
  • 2.82 AU (5:2 resonance)
  • 2.95 AU (7:3 resonance)
  • 3.27 AU (2:1 resonance), Hecuba gap, home to the Griqua group of asteroids.

Weaker and/or narrower gaps are also found at:

  • 1.90 AU (9:2 resonance)
  • 2.25 AU (7:2 resonance)
  • 2.33 AU (10:3 resonance)
  • 2.71 AU (8:3 resonance)
  • 3.03 AU (9:4 resonance)
  • 3.075 AU (11:5 resonance)
  • 3.47 AU (11:6 resonance)
  • 3.70 AU (5:3 resonance).

Asteroid zones

The gaps are not seen in a simple snapshot of the locations of the asteroids at any one time because asteroid orbits are elliptical, and many asteroids still cross through the radii corresponding to the gaps. The actual spatial density of asteroids in these gaps does not differ significantly from the neighboring regions.[5]

The main gaps occur at the 3:1, 5:2, 7:3, and 2:1 mean-motion resonances with Jupiter. An asteroid in the 3:1 Kirkwood gap would orbit the Sun three times for each Jovian orbit, for instance. Weaker resonances occur at other semi-major axis values, with fewer asteroids found than nearby. (For example, an 8:3 resonance for asteroids with a semi-major axis of 2.71 AU).[6]

The main or core population of the asteroid belt may be divided into the inner and outer zones, separated by the 3:1 Kirkwood gap at 2.5 AU, and the outer zone may be further divided into middle and outer zones by the 5:2 gap at 2.82 AU:[7]

  • 4:1 resonance (2.06 AU)
    • Zone I population (inner zone)
  • 3:1 resonance (2.5 AU)
    • Zone II population (middle zone)
  • 5:2 resonance gap (2.82 AU)
    • Zone III population (outer zone)
  • 2:1 resonance gap (3.28 AU)

4 Vesta is the largest asteroid in the inner zone, 1 Ceres and 2 Pallas in the middle zone, and 10 Hygiea in the outer zone. 87 Sylvia is probably the largest Main Belt asteroid beyond the outer zone.

See also

References
  1. Coleman, Helen Turnbull Waite (1956). Banners in the Wilderness: The Early Years of Washington and Jefferson College. University of Pittsburgh Press. p. 158. OCLC 2191890.
  2. Moons, Michèle; Morbidelli, Alessandro (1995). "Secular resonances inside mean-motion commensurabilities: the 4/1, 3/1, 5/2 and 7/3 cases". Icarus. 114 (1): 33–50. Bibcode:1995Icar..114...33M. doi:10.1006/icar.1995.1041.
  3. Moons, Michèle; Morbidelli, Alessandro; Migliorini, Fabio (1998). "Dynamical Structure of the 2/1 Commensurability with Jupiter and the Origin of the Resonant Asteroids". Icarus. 135 (2): 458–468. Bibcode:1998Icar..135..458M. doi:10.1006/icar.1998.5963.
  4. Minton, David A.; Malhotra, Renu (2009). "A record of planet migration in the main asteroid belt" (PDF). Nature. 457 (7233): 1109–1111. arXiv:0906.4574. Bibcode:2009Natur.457.1109M. doi:10.1038/nature07778. PMID 19242470. Retrieved 13 December 2016.
  5. McBride, N. & Hughes, D. W. (1990). "The spatial density of asteroids and its variation with asteroidal mass". Monthly Notices of the Royal Astronomical Society. 244: 513–520. Bibcode:1990MNRAS.244..513M.
  6. Ferraz-Mello, S. (June 14–18, 1993). "Kirkwood Gaps and Resonant Groups". proceedings of the 160th International Astronomical Union. Belgirate, Italy: Kluwer Academic Publishers. pp. 175–188. Bibcode:1994IAUS..160..175F.
  7. Klacka, Jozef (1992). "Mass distribution in the asteroid belt". Earth, Moon, and Planets. 56 (1): 47–52. Bibcode:1992EM&P...56...47K. doi:10.1007/BF00054599.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.