Lunar node

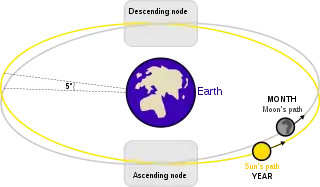
A lunar node is either of the two orbital nodes of the Moon, that is, the two points at which the orbit of the Moon intersects the ecliptic. The ascending (or north) node is where the Moon moves into the northern ecliptic hemisphere, while the descending (or south) node is where the Moon enters the southern ecliptic hemisphere.

The lunar nodes are the two points where the Moon's orbital path crosses the ecliptic, the Sun's apparent yearly path on the celestial sphere.

A lunar eclipse can occur only when the full Moon is near (within 11° 38' ecliptic longitude) either lunar node, while a solar eclipse can occur only when the new Moon is near (within 17° 25') either lunar node.

Because the orbital plane of the Moon precesses in space, the lunar nodes also precess around the ecliptic, completing one revolution (called a draconic or nodal period) in 18.612958 years (6,798.383 days). (This is not the same length as a saros.) The same cycle measured against an inertial frame of reference, such as International Celestial Reference System (ICRS), a coordinate system relative to the fixed stars, is 18.599525 years.

Both solar eclipses of July 2000 (on the 1st and 31st days) occurred around the time when the Moon was at its ascending node. Ascending-node eclipses recur after one draconic year on average, which is about 0.94901 Gregorian year, as do descending-node eclipses.

Names and symbols
The dragon in Peter Apian's Astronomicum Caesareum, 1540.

The nodes are called by different names in different cultures of the world.

In Hindu astronomy, the nodes are considered with the seven planets among the nine Navagrahas; the ascending node ☊ is called Rahu and the descending node ☋ is called Ketu.[1] In Tibetan astrology (partially based on the Kalachakra Tantra) these nodes are respectively named Rahu and Kalagni.[2]

In medieval texts, the nodes are referred to as ras wa dhanav al-tinnîn in Arabic. rosh ha-tely u-zenavo in Hebrew, and caput draconis (head of the dragon) or cauda draconis (tail of the dragon) in Latin.[3] The ascending node is referred to as the dragon's head with the astronomical or astrological symbol of ☊ and the descending node is known as the dragon's tail with the symbol ☋.

Declination extremes
See also: Lunar standstill

The Moon's orbit is inclined about 5.14° to the ecliptic; hence, the Moon can be up to about 5° north or south of the ecliptic. The ecliptic is inclined about 23.44° to the celestial equator, whose plane is perpendicular to the rotational axis of Earth. As a result, once during the 18.6-year nodal period (when the ascending node of the Moon's orbit coincides with the vernal equinox), the Moon's declination reaches a maximum and minimum (northern and southern extremes): about 28.6° from the celestial equator. Therefore, the moonrise or moonset azimuth has its northern- and southernmost points on the horizon; the Moon at culmination has its lowest and highest altitude (when the body transits the meridian); and first sightings of the new moon potentially have their latest times. Furthermore, occultations by the Moon of the Pleiades star cluster, which is over 4° north of the ecliptic, occur during a comparatively brief period once every nodal period.

Effect on tides

The precession of the lunar nodes has a small effect on Earth's tides – atmospheric, oceanic, or crustal.[4][5] The U.S. National Oceanic and Atmospheric Administration (NOAA) determines mean lower low water (MLLW) at a location by averaging the height of the lowest tide recorded at that location each day during a 19-year recording period, known as the National Tidal Datum Epoch.[6] The 19-year recording period is the nearest full-year count to the 18.6-year cycle of the lunar nodes.[7]

See also

References
  1. Hartner, Willy (1938), "The Pseudoplanetary Nodes of the Moon's Orbit in Hindu and Islamic Iconographies: A Contribution to the History of Ancient and Medieval Astrology", Ars Islamica, 5 (2): 112–154, JSTOR 4520926
  2. Berzin, Alexander (1987), "An Introduction to Tibetan Astronomy and Astrology", The Tibet Journal, 12 (1): 17–28, JSTOR 43300228
  3. Sela, Shlomo (2003), Abraham Ibn Ezra and the Rise of Medieval Hebrew Science, Brill's Series in Jewish Studies, 32, Leiden / Boston: Brill, pp. 124–126, 244–245, ISBN 9789004129733
  4. Godin, G. (2015). The Use of Nodal Corrections in the Calculation of Harmonic Constants. The International Hydrographic Review, 63(2). Retrieved from https://journals.lib.unb.ca/index.php/ihr/article/view/23428
  5. Kaye, Clifford A.; Stuckey, Gary W. (1973). "Nodal Tidal Cycle of 18.6 Yr.: Its Importance in Sea-Level Curves of the East Coast of the United States and Its Value in Explaining Long-Term Sea-Level Changes". Geology. 1 (3): 141. doi:10.1130/0091-7613(1973)1<141:NTCOYI>2.0.CO;2. ISSN 0091-7613.
  6. "Tidal Datums". Tides and Currents. NOAA.
  7. "Tidal Datums and Their Applications" (PDF). Tides and Currents. Silver Spring, MD: NOAA (Special Publication NOS CO-OPS 1). June 2000.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.