RC5
In cryptography, RC5 is a symmetric-key block cipher notable for its simplicity. Designed by Ronald Rivest in 1994,[2] RC stands for "Rivest Cipher", or alternatively, "Ron's Code" (compare RC2 and RC4). The Advanced Encryption Standard (AES) candidate RC6 was based on RC5.
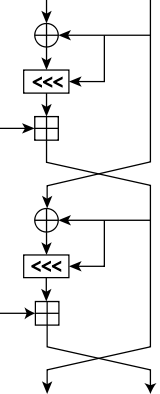 One round (two half-rounds) of the RC5 block cipher | |
| General | |
|---|---|
| Designers | Ron Rivest |
| First published | 1994 |
| Successors | RC6, Akelarre |
| Cipher detail | |
| Key sizes | 0 to 2040 bits (128 suggested) |
| Block sizes | 32, 64 or 128 bits (64 suggested) |
| Structure | Feistel-like network |
| Rounds | 1-255 (12 suggested originally) |
| Best public cryptanalysis | |
| 12-round RC5 (with 64-bit blocks) is susceptible to a differential attack using 244 chosen plaintexts.[1] | |
Description
Unlike many schemes, RC5 has a variable block size (32, 64 or 128 bits), key size (0 to 2040 bits) and number of rounds (0 to 255). The original suggested choice of parameters were a block size of 64 bits, a 128-bit key and 12 rounds.
A key feature of RC5 is the use of data-dependent rotations; one of the goals of RC5 was to prompt the study and evaluation of such operations as a cryptographic primitive . RC5 also consists of a number of modular additions and eXclusive OR (XOR)s. The general structure of the algorithm is a Feistel-like network. The encryption and decryption routines can be specified in a few lines of code. The key schedule, however, is more complex, expanding the key using an essentially one-way function with the binary expansions of both e and the golden ratio as sources of "nothing up my sleeve numbers". The tantalising simplicity of the algorithm together with the novelty of the data-dependent rotations has made RC5 an attractive object of study for cryptanalysts. The RC5 is basically denoted as RC5-w/r/b where w=word size in bits, r=number of rounds, b=number of 8-bit bytes in the key.
Algorithm
RC5 encryption and decryption both expand the random key into 2(r+1) words that will be used sequentially (and only once each) during the encryption and decryption processes. All of the below comes from Rivest's revised paper on RC5.[3]
Key expansion
The key expansion algorithm is illustrated below, first in pseudocode, then example C code copied directly from the reference paper's appendix.
Following the naming scheme of the paper, the following variable names are used:
- w - The length of a word in bits, typically 16, 32 or 64. Encryption is done in 2-word blocks.
- u = w/8 - The length of a word in bytes.
- b - The length of the key in bytes.
- K[] - The key, considered as an array of bytes (using 0-based indexing).
- c - The length of the key in words (or 1, if b = 0).
- L[] - A temporary working array used during key scheduling. initialized to the key in words.
- r - The number of rounds to use when encrypting data.
- t = 2(r+1) - the number of round subkeys required.
- S[] - The round subkey words.
- Pw - The first magic constant, defined as , where Odd is the nearest odd integer to the given input, e is the base of the natural logarithm, and w is defined above. For common values of w, the associated values of Pw are given here in hexadecimal:
- For w = 16: 0xB7E1
- For w = 32: 0xB7E15163
- For w = 64: 0xB7E151628AED2A6B
- Qw - The second magic constant, defined as , where Odd is the nearest odd integer to the given input, where is the golden ratio, and w is defined above. For common values of w, the associated values of Qw are given here in hexadecimal:
- For w = 16: 0x9E37
- For w = 32: 0x9E3779B9
- For w = 64: 0x9E3779B97F4A7C15
# Break K into words
# u = w / 8
c = ceiling(max(b, 1) / u)
# L is initially a c-length list of 0-valued w-length words
for i = b-1 down to 0 do:
L[i / u] = (L[i / u] <<< 8) + K[i]
# Initialize key-independent pseudorandom S array
# S is initially a t=2(r+1) length list of undefined w-length words
S[0] = P_w
for i = 1 to t-1 do:
S[i] = S[i - 1] + Q_w
# The main key scheduling loop
i = j = 0
A = B = 0
do 3 * max(t, c) times:
A = S[i] = (S[i] + A + B) <<< 3
B = L[j] = (L[j] + A + B) <<< (A + B)
i = (i + 1) % t
j = (j + 1) % c
# return S
The example source code is provided from the appendix of Rivest's paper on RC5. The implementation is designed to work with w = 32, r = 12, and b = 16.
void RC5_SETUP(unsigned char *K)
{
// w = 32, r = 12, b = 16
// c = max(1, ceil(8 * b/w))
// t = 2 * (r+1)
WORD i, j, k, u = w/8, A, B, L[c];
for (i = b-1, L[c-1] = 0; i != -1; i--)
L[i/u] = (L[i/u] << 8) + K[i];
for (S[0] = P, i = 1; i < t; i++)
S[i] = S[i-1] + Q;
for (A = B = i = j = k = 0; k < 3 * t; k++, i = (i+1) % t, j = (j+1) % c)
{
A = S[i] = ROTL(S[i] + (A + B), 3);
B = L[j] = ROTL(L[j] + (A + B), (A + B));
}
}
Encryption
Encryption involved several rounds of a simple function. 12 or 20 rounds seem to be recommended, depending on security needs and time considerations. Beyond the variables used above, the following variables are used in this algorithm:
- A, B - The two words composing the block of plaintext to be encrypted.
A = A + S[0]
B = B + S[1]
for i = 1 to r do:
A = ((A ^ B) <<< B) + S[2 * i]
B = ((B ^ A) <<< A) + S[2 * i + 1]
# The ciphertext block consists of the two-word wide block composed of A and B, in that order.
return A, B
The example C code given by Rivest is this.
void RC5_ENCRYPT(WORD *pt, WORD *ct)
{
WORD i, A = pt[0] + S[0], B = pt[1] + S[1];
for (i = 1; i <= r; i++)
{
A = ROTL(A ^ B, B) + S[2*i];
B = ROTL(B ^ A, A) + S[2*i + 1];
}
ct[0] = A; ct[1] = B;
}
Decryption
Decryption is a fairly straightforward reversal of the encryption process. The below pseudocode shows the process.
for i = r down to 1 do:
B = ((B - S[2 * i + 1]) >>> A) ^ A
A = ((A - S[2 * i]) >>> B) ^ B
B = B - S[1]
A = A - S[0]
return A, B
The example C code given by Rivest is this.
void RC5_DECRYPT(WORD *ct, WORD *pt)
{
WORD i, B=ct[1], A=ct[0];
for (i = r; i > 0; i--)
{
B = ROTR(B - S[2*i + 1], A) ^ A;
A = ROTR(A - S[2*i], B) ^ B;
}
pt[1] = B - S[1]; pt[0] = A - S[0];
}
Cryptanalysis
12-round RC5 (with 64-bit blocks) is susceptible to a differential attack using 244 chosen plaintexts.[1] 18–20 rounds are suggested as sufficient protection.
A number of these challenge problems have been tackled using distributed computing, organised by Distributed.net. Distributed.net has brute-forced RC5 messages encrypted with 56-bit and 64-bit keys and has been working on cracking a 72-bit key since November 3, 2002.[4] As of December 13, 2019, 6.222% of the keyspace has been searched and based on the rate recorded that day, it would take 102 years to complete 100% of the keyspace.[5] The task has inspired many new and novel developments in the field of cluster computing.[6]
RSA Security, which had a patent on the algorithm,[7] offered a series of US$10,000 prizes for breaking ciphertexts encrypted with RC5, but these contests have been discontinued as of May 2007.[8] As a result, distributed.net decided to fund the monetary prize. The individual who discovers the winning key will receive US$1,000, their team (if applicable) will receive US$1,000 and the Free Software Foundation will receive US$2,000.[9]
References
- Biryukov A. and Kushilevitz E. (1998). Improved Cryptanalysis of RC5. EUROCRYPT 1998.
- Rivest, R. L. (1994). "The RC5 Encryption Algorithm" (PDF). Proceedings of the Second International Workshop on Fast Software Encryption (FSE) 1994e. pp. 86–96.
- http://people.csail.mit.edu/rivest/Rivest-rc5rev.pdf
- "distributed.net: Project RC5". www.distributed.net. Retrieved 14 December 2019.
- RC5-72 / Overall Project Stats
- "Archived copy". Archived from the original on 2014-10-28. Retrieved 2014-10-28.CS1 maint: archived copy as title (link)
- Rivest, R. L, "Block Encryption Algorithm With Data Dependent Rotation", U.S. Patent 5,724,428, issued on 3 March 1998.
- "distributed.net: Project RC5". www.distributed.net. Retrieved 14 December 2019.
- "distributed.net: staff blogs – 2008 – September – 08". Retrieved 15 December 2019.
