Van der Waals surface

The Van der Waals surface of a molecule is an abstract representation or model of that molecule, illustrating where, in very rough terms, a surface might reside for the molecule based on the hard cutoffs of Van der Waals radii for individual atoms, and it represents a surface through which the molecule might be conceived as interacting with other molecules. Also referred to as a Van der Waals envelope, the Van der Waals surface is named for Johannes Diderik van der Waals, a Dutch theoretical physicist and thermodynamicist who developed theory to provide a liquid-gas equation of state that accounted for the non-zero volume of atoms and molecules, and on their exhibiting an attractive force when they interacted (theoretical constructions that also bear his name). Van der Waals surfaces are therefore a tool used in the abstract representations of molecules, whether accessed, as they were originally, via hand calculation, or via physical wood/plastic models, or now digitally, via computational chemistry software. Practically speaking, CPK models, developed by and named for Robert Corey, Linus Pauling, and Walter Koltun,[3] were the first widely used physical molecular models based on Van der Waals radii, and allowed broad pedagogical and research use of a model showing the Van der Waals surfaces of molecules.

Van der Waals radii
Elementradius (Å)
Hydrogen1.2 (1.09)[1]
Carbon1.7
Nitrogen1.55
Oxygen1.52
Fluorine1.47
Phosphorus1.8
Sulfur1.8
Chlorine1.75
Copper1.4
Van der Waals radii taken from
Bondi's compilation (1964).[2]
Values from other sources may
differ significantly (see text)

Van der Waals volume and Van der Waals surface area
Methane, CH4, space-filling, Van der Waal's-based representation, carbon (C ) in black, hydrogen (H) in white. In chemistry, a space-filling model is a type of three-dimensional (3D) molecular model where the atoms are represented by spheres whose radii are, either as Van der Waals radii or otherwise, proportional to the radii of the atoms. Center-to-center distances of the atoms are proportional to the distances between the atomic nuclei, all in the same scale. Atoms of different chemical elements are usually represented by spheres of different colors, see below.

Related to the title concept are the ideas of a Van der Waals volume, Vw, and a Van der Waals surface area, abbreviated variously as Aw, vdWSA, VSA, and WSA. A Van der Waals surface area is an abstract conception of the surface area of atoms or molecules from a mathematical estimation, either computing it from first principles or by integrating over a corresponding Van der Waals volume. In simplest case, for a spherical monatomic gas, it is simply the computed surface area of a sphere of radius equal to the Van der Waals radius of the gaseous atom:

.

The Van der Waals volume, a type of atomic or molecular volume, is a property directly related to the Van der Waals radius, and is defined as the volume occupied by an individual atom, or in a combined sense, by all atoms of a molecule. It may be calculated for atoms if the Van der Waals radius is known, and for molecules if its atoms radii and the inter-atomic distances and angles are known. As above, in simplest case, for a spherical monatomic gas, Vw is simply the computed volume of a sphere of radius equal to the Van der Waals radius of the gaseous atom:

.

For a molecule, Vw is the volume enclosed by the Van der Waals surface; hence, computation of Vw presumes ability to describe and compute a Van der Waals surface. Van der Waals volumes of molecules are always smaller than the sum of the Van der Waals volumes of their constituent atoms, due to the fact that the interatomic distances resulting from chemical bond are less than the sum of the atomic Van der Waals radii. In this sense, a Van der Waals surface of a homonuclear diatomic molecule can be viewed as an pictorial overlap of the two spherical Van der Waals surfaces of the individual atoms, likewise for larger molecules like methane, ammonia, etc. (see images).

Van der Waals radii and volumes may be determined from the mechanical properties of gases (the original method, determining the Van der Waals constant), from the critical point (e.g., of a fluid), from crystallographic measurements of the spacing between pairs of unbonded atoms in crystals, or from measurements of electrical or optical properties (i.e., polarizability or molar refractivity). In all cases, measurements are made on macroscopic samples and results are expressed as molar quantities. Van der Waals volumes of a single atom or molecules are arrived at by dividing the macroscopically determined volumes by the Avogadro constant. The various methods give radius values which are similar, but not identical—generally within 1–2 Å (100–200 pm). Useful tabulated values of Van der Waals radii are obtained by taking a weighted mean of a number of different experimental values, and, for this reason, different tables will be seen to present different values for the Van der Waals radius of the same atom. As well, it has been argued that the Van der Waals radius is not a fixed property of an atom in all circumstances, rather, that it will vary with the chemical environment of the atom.[2]

  • Ammonia, NH3, space-filling, Van der Waal's-based representation, nitrogen (N) in blue, hydrogen (H) in white.
  • Phosphine, PH3, space-filling, Van der Waal's-based representation, ball-and-stick model superimposed, phosphorus (P) in orange, hydrogen (H) in white.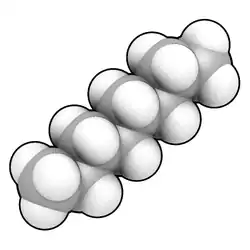
  • A space-filling model of n-octane, the straight chain (normal) hydrocarbon composed of 8 carbons and 18 hydrogens, formulae: CH3CH2(CH2)4CH2CH3 or C
    8    H
    18    . Note, the representative shown is of a single conformational "pose" of a population of molecules, which, because of low Gibbs energy barriers to rotation about its carbon-carbon bonds (giving the carbon "chain" great flexibility). normally is composed of a very large number of different such conformations (e.g., in solution).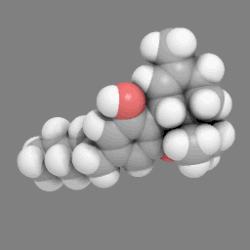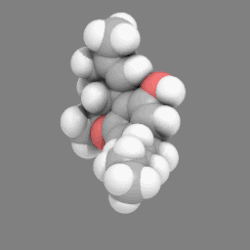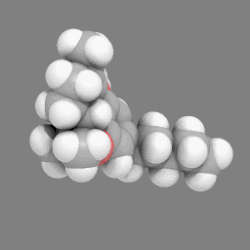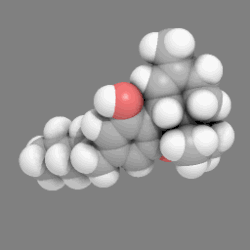
  • An example of a three-dimensional, space-filling, Van der Waal's-based model of a complex molecule, THC, the active agent in medical marijuana. You may need to click on the image to see rotation.
  • Hydrogen sulfide, H2S, space-filling, Van der Waal's-based representation, ball-and-stick model superimposed, sulfur (S) in yellow, hydrogen (H) in white over-shaded with blue. It also shows on it surface the electrostatic potential surface, computed for the molecule in unknown fashion, using computational chemistry tools. It is shaded from blue for electropositive areas to red for electronegative areas.

See also

Further reading

References and notes
  1. Rowland RS, Taylor R (1996). "Intermolecular nonbonded contact distances in organic crystal structures: comparison with distances expected from Van der Waals radii". J. Phys. Chem. 100 (18): 7384–7391. doi:10.1021/jp953141+.
  2. Bondi, A. (1964). "Van der Waals Volumes and Radii". J. Phys. Chem. 68 (3): 441–51. doi:10.1021/j100785a001.
  3. Robert B. Corey & Linus Pauling, 1953, "Molecular models of amino acids, peptides, and proteins," Rev. Sci. Instrum., 24(8), pp. 621–627, DOI 10.1063/1.1770803, see , accessed 23 June 2015.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.