Legendre transformation

In mathematics and physics, the Legendre transformation, named after Adrien-Marie Legendre, is an involutive transformation on the real-valued convex functions of one real variable. In physical problems, it is used to convert functions of one quantity (such as position, pressure, or temperature) into functions of the conjugate quantity (momentum, volume, and entropy, respectively). In this way, it is commonly used in classical mechanics to derive the Hamiltonian formalism out of the Lagrangian formalism and in thermodynamics to derive the thermodynamic potentials, as well as in the solution of differential equations of several variables.

The function

f(x)

is defined on the interval

[a,b]

. The difference

px-f(x)

takes a maximum at

x

. Thus,

f^{*}(p)=px^{\prime }-f(x^{\prime })

.

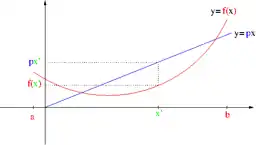
For sufficiently smooth functions on the real line, the Legendre transform $f^{*}$ of a function $f$ can be specified, up to an additive constant, by the condition that the functions' first derivatives are inverse functions of each other. This can be expressed in Euler's derivative notation as

Df(\cdot )=\left(Df^{*}\right)^{-1}(\cdot )~,

where

(\phi )^{-1}(\cdot )

means a function such that

(\phi )^{-1}(\phi (x))=x~,

or, equivalently, as $f'(f^{*\prime }(x^{*}))=x^{*}$ and $f^{*\prime }(f'(x))=x$ in Lagrange's notation.

The generalization of the Legendre transformation to affine spaces and non-convex functions is known as the convex conjugate (also called the Legendre–Fenchel transformation), which can be used to construct a function's convex hull.

Definition

Let $I\subset \mathbb {R}$ be an interval, and $f:I\to \mathbb {R}$ a convex function; then its Legendre transform is the function $f^{*}:I^{*}\to \mathbb {R}$ defined by

f^{*}(x^{*})=\sup _{x\in I}(x^{*}x-f(x)),\quad x^{*}\in I^{*}

where $\sup$ denotes the supremum, and the domain $I^{*}$ is

I^{*}=\left\{x^{*}\in \mathbb {R

The transform is always well-defined when $f(x)$ is convex.

The generalization to convex functions $f:X\to \mathbb {R}$ on a convex set $X\subset \mathbb {R} ^{n}$ is straightforward: $f^{*}:X^{*}\to \mathbb {R}$ has domain

X^{*}=\left\{x^{*}\in \mathbb {R} ^{n}:\sup _{x\in X}(\langle x^{*},x\rangle -f(x))<\infty \right\}

and is defined by

f^{*}(x^{*})=\sup _{x\in X}(\langle x^{*},x\rangle -f(x)),\quad x^{*}\in X^{*}~,

where $\langle x^{*},x\rangle$ denotes the dot product of $x^{*}$ and $x$ .

The function $f^{*}$ is called the convex conjugate function of $f$ . For historical reasons (rooted in analytic mechanics), the conjugate variable is often denoted $p$ , instead of $x^{*}$ . If the convex function $f$ is defined on the whole line and is everywhere differentiable, then

f^{*}(p)=\sup _{x\in I}(px-f(x))=\left(px-f(x)\right)|_{x=(f')^{-1}(p)}

can be interpreted as the negative of the $y$ -intercept of the tangent line to the graph of $f$ that has slope $p$ .

The Legendre transformation is an application of the duality relationship between points and lines. The functional relationship specified by $f$ can be represented equally well as a set of $(x,y)$ points, or as a set of tangent lines specified by their slope and intercept values.

Understanding the transform in terms of derivatives

For a differentiable convex function $f$ on the real line with an invertible first derivative, the Legendre transform $f^{*}$ can be specified, up to an additive constant, by the condition that the functions' first derivatives are inverse functions of each other. Explicitly, for a differentiable convex function $f$ on the real line with a first derivative $f'$ with inverse $(f')^{-1}$ , the Legendre transform $f^{*}$ (with derivative $(f^{*})'$ with inverse $((f^{*})^{\prime })^{-1}$ ) can be specified, up to an additive constant, by the condition that $f'$ and $(f^{*})^{\prime }$ are inverse functions of each other, i.e., $f'=((f^{*})^{\prime })^{-1}$ and $(f^{*})^{\prime }=(f')^{-1}$ .

To see this, first note that if $f$ is differentiable and ${\overline {x}}$ is a critical point of the function of $x\mapsto p\cdot x-f(x)$ , then the supremum is achieved at ${\overline {x}}$ (by convexity). Therefore, $f^{*}(p)=p\cdot {\overline {x}}-f({\overline {x}})$ .

Suppose that $f'$ is invertible and let $h$ denote its inverse. Then for each $p$ , the point $h(p)$ is the unique critical point of $x\mapsto px-f(x)$ . Indeed, $f'(h(p))=p$ and so $p-f'(h(p))=0$ . Hence we have $f^{*}(p)=p\cdot h(p)-f(h(p))$ for each $p$ . By differentiating with respect to $p$ we find

(f^{*})'(p)=h(p)+p\cdot h'(p)-f'(h(p))\cdot h'(p).

Since $f'(h(p))=p$ this simplifies to $(f^{*})'(p)=h(p)$ . In other words, $(f^{*})'$ and $f'$ are inverses.

In general, if $g'$ is an inverse of $f'$ , then $g'=(f^{*})'$ and so integration provides a constant $c$ so that $f^{*}=g+c$ .

In practical terms, given $f(x)$ , the parametric plot of $xf'(x)-f(x)$ versus $f'(x)$ amounts to the graph of $g(p)$ versus $p$ .

In some cases (e.g. thermodynamic potentials, below), a non-standard requirement is used, amounting to an alternative definition of $f *$ with a minus sign,

f(x)-f^{*}(p)=xp.

Properties

The Legendre transform of a convex function is convex.

Let us show this for the case of a doubly differentiable

f

with a non zero (and hence positive, due to convexity) double derivative.

For a fixed

p

, let

x

maximize

px - f (x)

. Then

f *(p) = px - f (x)

, noting that

x

depends on

p

. Thus,

f^{\prime }(x)=p~.

The derivative of

f

is itself differentiable with a positive derivative and hence strictly monotonic and invertible.

Thus

x = g (p)

where

g\equiv (f^{\prime })^{-1}

, meaning that

g

is defined so that

f'(g(p))=p

.

Note that

g

is also differentiable with the following derivative,

{\frac {dg(p)}{dp}}={\frac {1}{f''(g(p))}}~.

Thus

f *(p) = pg (p) - f (g (p))

is the composition of differentiable functions, hence differentiable.

Applying the product rule and the chain rule yields

{\begin{aligned}{\frac {d(f^{*})}{dp}}&=g(p)+\left(p-f'(g(p))\right)\cdot {\frac {dg(p)}{dp}}\\[4pt]&=g(p),\end{aligned}}

giving

{\frac {d^{2}(f^{*})}{dp^{2}}}={\frac {dg(p)}{dp}}={\frac {1}{f''(g(p))}}>0,

so

f *

is convex.

It follows that the Legendre transformation is an involution, i.e., $f ** = f$ :

By using the above equalities for

g (p)

,

f *(p)

and its derivative,

{\begin{aligned}f^{**}(x)&{}=\left(x\cdot p_{s}-f^{*}(p_{s})\right)_{|{\frac {d}{dp}}f^{*}(p=p_{s})=x}\\[5pt]&{}=g(p_{s})\cdot p_{s}-f^{*}(p_{s})\\[5pt]&{}=f(g(p_{s}))\\[5pt]&{}=f(x)~.\end{aligned}}

Examples

Example 1

e^x is plotted in red and its Legendre transform in dashed blue.

The exponential function $f(x)=e^{x}$ has $f^{*}(p)=p(\ln p-1)$ as a Legendre transform, since their respective first derivatives $e x$ and $ln p$ are inverse functions of each other.

This example illustrates that the respective domains of a function and its Legendre transform need not agree.

Example 2

Let $f (x) = cx 2$ defined on ℝ, where $c > 0$ is a fixed constant.

For $x *$ fixed, the function of $x$ , $x * x - f (x) = x * x - cx 2$ has the first derivative $x * - 2 cx$ and second derivative $-2 c$ ; there is one stationary point at $x = x */2 c$ , which is always a maximum.

Thus, $I * = ℝ$ and

f^{*}(x^{*})={\frac {{x^{*}}^{2}}{4c}}~.

The first derivatives of $f$ , 2 $cx$ , and of $f *$ , $x */(2 c)$ , are inverse functions to each other. Clearly, furthermore,

f^{**}(x)={\frac {1}{4(1/4c)}}x^{2}=cx^{2}~,

namely $f ** = f$ .

Example 3

Let $f (x) = x 2$ for $x \in I = [2, 3]$ .

For $x *$ fixed, $x * x - f (x)$ is continuous on $I$ compact, hence it always takes a finite maximum on it; it follows that $I * = ℝ$ .

The stationary point at $x = x */2$ is in the domain $[2, 3]$ if and only if $4 \leq x * \leq 6$ , otherwise the maximum is taken either at $x = 2$ , or $x = 3$ . It follows that

f^{*}(x^{*})={\begin{cases}2x^{*}-4,&x^{*}<4\\{\frac {{x^{*}}^{2}}{4}},&4\leqslant x^{*}\leqslant 6,\\3x^{*}-9,&x^{*}>6.\end{cases}}

Example 4

The function $f (x) = cx$ is convex, for every $x$ (strict convexity is not required for the Legendre transformation to be well defined). Clearly $x * x - f (x) = (x * - c) x$ is never bounded from above as a function of $x$ , unless $x * - c = 0$ . Hence $f *$ is defined on $I * = {c$ } and $f *(c) = 0$ .

One may check involutivity: of course $x * x - f *(x *)$ is always bounded as a function of $x * \in {c$ }, hence $I ** = ℝ$ . Then, for all $x$ one has

\sup _{x^{*}\in \{c\}}(xx^{*}-f^{*}(x^{*}))=xc,

and hence $f **(x) = cx = f (x)$ .

Example 5: several variables

Let

f(x)=\langle x,Ax\rangle +c

be defined on $X = ℝ n$ , where $A$ is a real, positive definite matrix.

Then $f$ is convex, and

\langle p,x\rangle -f(x)=\langle p,x\rangle -\langle x,Ax\rangle -c,

has gradient $p - 2 Ax$ and Hessian $-2 A$ , which is negative; hence the stationary point $x = A -1 p /2$ is a maximum.

We have $X * = ℝ n$ , and

f^{*}(p)={\frac {1}{4}}\langle p,A^{-1}p\rangle -c.

Behavior of differentials under Legendre transforms

The Legendre transform is linked to integration by parts, $pdx = d (px) - xdp$ .

Let $f$ be a function of two independent variables $x$ and $y$ , with the differential

df={\partial f \over \partial x}\,dx+{\partial f \over \partial y}\,dy=p\,dx+v\,dy.

Assume that it is convex in $x$ for all $y$ , so that one may perform the Legendre transform in $x$ , with $p$ the variable conjugate to $x$ . Since the new independent variable is $p$ , the differentials $dx$ and $dy$ devolve to $dp$ and $dy$ , i.e., we build another function with its differential expressed in terms of the new basis $dp$ and $dy$ .

We thus consider the function $g (p, y) = f - px$ so that

dg=df-p\,dx-x\,dp=-x\,dp+v\,dy

x=-{\frac {\partial g}{\partial p}}

v={\frac {\partial g}{\partial y}}.

The function $-g (p, y)$ is the Legendre transform of $f (x, y)$ , where only the independent variable $x$ has been supplanted by $p$ . This is widely used in thermodynamics, as illustrated below.

Applications

Analytical mechanics

A Legendre transform is used in classical mechanics to derive the Hamiltonian formulation from the Lagrangian formulation, and conversely. A typical Lagrangian has the form

L(v,q)={\tfrac {1}{2}}\langle v,Mv\rangle -V(q),

where $(v,q)$ are coordinates on $R n \times R n$ , $M$ is a positive real matrix, and

\langle x,y\rangle =\sum _{j}x_{j}y_{j}.

For every $q$ fixed, $L(v,q)$ is a convex function of $v$ , while $V(q)$ plays the role of a constant.

Hence the Legendre transform of $L(v,q)$ as a function of $v$ is the Hamiltonian function,

H(p,q)={\tfrac {1}{2}}\langle p,M^{-1}p\rangle +V(q)

.

In a more general setting, $(v,q)$ are local coordinates on the tangent bundle $T{\mathcal {M}}$ of a manifold ${\mathcal {M}}$ . For each $q$ , $L(v,q)$ is a convex function of the tangent space $V q$ . The Legendre transform gives the Hamiltonian $H(p,q)$ as a function of the coordinates $(p, q)$ of the cotangent bundle $T^{*}{\mathcal {M}}$ ; the inner product used to define the Legendre transform is inherited from the pertinent canonical symplectic structure. In this abstract setting, the Legendre transformation corresponds to the tautological one-form.

Thermodynamics

The strategy behind the use of Legendre transforms in thermodynamics is to shift from a function that depends on a variable to a new (conjugate) function that depends on a new variable, the conjugate of the original one. The new variable is the partial derivative of the original function with respect to the original variable. The new function is the difference between the original function and the product of the old and new variables. Typically, this transformation is useful because it shifts the dependence of, e.g., the energy from an extensive variable to its conjugate intensive variable, which can usually be controlled more easily in a physical experiment.

For example, the internal energy is an explicit function of the extensive variables entropy, volume, and chemical composition

U=U\left(S,V,\{N_{i}\}\right),

which has a total differential

dU=T\,dS-P\,dV+\sum \mu _{i}\,dN_{i}.

Stipulating some common reference state, by using the (non-standard) Legendre transform of the internal energy, $U$ , with respect to volume, $V$ , the enthalpy may be defined by writing

H=U+PV=H(S,P,\{N_{i}\}),

which is now explicitly function of the pressure $P$ , since

dH(S,P,\{N_{i}\})=T\,dS+V\,dP+\sum \mu _{i}\,dN_{i}.

The enthalpy is suitable for description of processes in which the pressure is controlled from the surroundings.

It is likewise possible to shift the dependence of the energy from the extensive variable of entropy, $S$ , to the (often more convenient) intensive variable $T$ , resulting in the Helmholtz and Gibbs free energies. The Helmholtz free energy, $A$ , and Gibbs energy, $G$ , are obtained by performing Legendre transforms of the internal energy and enthalpy, respectively,

A=U-TS~,

G=H-TS=U+PV-TS~.

The Helmholtz free energy is often the most useful thermodynamic potential when temperature and volume are controlled from the surroundings, while the Gibbs energy is often the most useful when temperature and pressure are controlled from the surroundings.

An example – variable capacitor

As another example from physics, consider a parallel-plate capacitor, in which the plates can move relative to one another. Such a capacitor would allow transfer of the electric energy which is stored in the capacitor into external mechanical work, done by the force acting on the plates. One may think of the electric charge as analogous to the "charge" of a gas in a cylinder, with the resulting mechanical force exerted on a piston.

Compute the force on the plates as a function of $x$ , the distance which separates them. To find the force, compute the potential energy, and then apply the definition of force as the gradient of the potential energy function.

The energy stored in a capacitor of capacitance $C (x)$ and charge $Q$ is

U(Q,\mathbf {x} )={\frac {1}{2}}QV={\frac {1}{2}}{\frac {Q^{2}}{C(\mathbf {x} )}},~

where the dependence on the area of the plates, the dielectric constant of the material between the plates, and the separation $x$ are abstracted away as the capacitance $C (x)$ . (For a parallel plate capacitor, this is proportional to the area of the plates and inversely proportional to the separation.)

The force $F$ between the plates due to the electric field is then

\mathbf {F} (\mathbf {x} )=-{\frac {dU}{d\mathbf {x} }}~.

If the capacitor is not connected to any circuit, then the charges on the plates remain constant as they move, and the force is the negative gradient of the electrostatic energy

\mathbf {F} (\mathbf {x} )={\frac {1}{2}}{\frac {dC}{d\mathbf {x} }}{\frac {Q^{2}}{C^{2}}}.

However, suppose, instead, that the voltage between the plates $V$ is maintained constant by connection to a battery, which is a reservoir for charge at constant potential difference; now the charge is variable instead of the voltage, its Legendre conjugate. To find the force, first compute the non-standard Legendre transform,

U^{*}=U-\left({\frac {\partial U}{\partial Q}}\right){\bigg |}_{\mathbf {x} }\cdot Q=U-{\frac {1}{2C(\mathbf {x} )}}\left({\frac {\partial Q^{2}}{\partial Q}}\right){\bigg |}_{\mathbf {x} }\cdot Q=U-QV={\frac {1}{2}}QV-QV=-{\frac {1}{2}}QV=-{\tfrac {1}{2}}V^{2}C(\mathbf {x} ).

The force now becomes the negative gradient of this Legendre transform, still pointing in the same direction,

\mathbf {F} (\mathbf {x} )=-{\frac {dU^{*}}{d\mathbf {x} }}~.

The two conjugate energies happen to stand opposite to each other, only because of the linearity of the capacitance—except now $Q$ is no longer a constant. They reflect the two different pathways of storing energy into the capacitor, resulting in, for instance, the same "pull" between a capacitor's plates.

Probability theory

In large deviations theory, the rate function is defined as the Legendre transformation of the logarithm of the moment generating function of a random variable. An important application of the rate function is in the calculation of tail probabilities of sums of i.i.d. random variables.

Microeconomics

Legendre transformation arises naturally in microeconomics in the process of finding the supply $S (P)$ of some product given a fixed price $P$ on the market knowing the cost function $C (Q)$ , i.e. the cost for the producer to make/mine/etc. $Q$ units of the given product.

A simple theory explains the shape of the supply curve based solely on the cost function. Let us suppose the market price for a one unit of our product is $P$ . For a company selling this good, the best strategy is to adjust the production $Q$ so that its profit is maximized. We can maximize the profit

{\text{profit}}={\text{revenue}}-{\text{costs}}=PQ-C(Q)

by differentiating with respect to $Q$ and solving

P-C'(Q_{opt})=0.

$Q opt$ represents the optimal quantity $Q$ of goods that the producer is willing to supply, which is indeed the supply itself:

S(P)=Q_{opt}(P)=(C^{'})^{-1}(P)

.

If we consider the maximal profit as a function of price, ${\text{profit}}_{\text{max}}(P)$ , we see that it is the Legendre transform of the cost function $C(Q)$ .

Geometric interpretation

For a strictly convex function, the Legendre transformation can be interpreted as a mapping between the graph of the function and the family of tangents of the graph. (For a function of one variable, the tangents are well-defined at all but at most countably many points, since a convex function is differentiable at all but at most countably many points.)

The equation of a line with slope $p$ and $y$ -intercept $b$ is given by $y=px+b.$ For this line to be tangent to the graph of a function $f$ at the point $\left(x_{0},f\left(x_{0}\right)\right)$ requires

f\left(x_{0}\right)=px_{0}+b

and

p=f^{\prime }\left(x_{0}\right).

Being the derivative of a strictly convex function, the function $f^{\prime }$ is strictly monotone and thus injective. The second equation can be solved for $x_{0}=f^{\prime -1}(p),$ allowing elimination of $x_{0}$ from the first, and solving for the $y$ -intercept $b$ of the tangent as a function of its slope $p,$

b=f\left(x_{0}\right)-px_{0}=f\left(f^{\prime -1}(p)\right)-p\cdot f^{\prime -1}(p)=-f^{\star }(p)

where $f^{\star }$ denotes the Legendre transform of $f.$

The family of tangent lines of the graph of $f$ parameterized by the slope $p$ is therefore given by

y=px-f^{\star }(p),

or, written implicitly, by the solutions of the equation

F(x,y,p)=y+f^{\star }(p)-px=0~.

The graph of the original function can be reconstructed from this family of lines as the envelope of this family by demanding

{\partial F(x,y,p) \over \partial p}=f^{\star \prime }(p)-x=0.

Eliminating $p$ from these two equations gives

y=x\cdot f^{\star \prime -1}(x)-f^{\star }\left(f^{\star \prime -1}(x)\right).

Identifying $y$ with $f(x)$ and recognizing the right side of the preceding equation as the Legendre transform of $f^{\star },$ yields

f(x)=f^{\star \star }(x)~.

Legendre transformation in more than one dimension

For a differentiable real-valued function on an open subset $U$ of $R n$ the Legendre conjugate of the pair $(U, f)$ is defined to be the pair $(V, g)$ , where $V$ is the image of $U$ under the gradient mapping $Df$ , and $g$ is the function on $V$ given by the formula

g(y)=\left\langle y,x\right\rangle -f(x),\qquad x=\left(Df\right)^{-1}(y)

where

\left\langle u,v\right\rangle =\sum _{k=1}^{n}u_{k}\cdot v_{k}

is the scalar product on $R n$ . The multidimensional transform can be interpreted as an encoding of the convex hull of the function's epigraph in terms of its supporting hyperplanes.[1]

Alternatively, if $X$ is a vector space and $Y$ is its dual vector space, then for each point $x$ of $X$ and $y$ of $Y$ , there is a natural identification of the cotangent spaces $T* X x$ with $Y$ and $T* Y y$ with $X$ . If $f$ is a real differentiable function over $X$ , then its exterior derivative, $df$ , is a section of the cotangent bundle $T* X$ and as such, we can construct a map from $X$ to $Y$ . Similarly, if $g$ is a real differentiable function over $Y$ , then $dg$ defines a map from $Y$ to $X$ . If both maps happen to be inverses of each other, we say we have a Legendre transform. The notion of the tautological one-form is commonly used in this setting.

When the function is not differentiable, the Legendre transform can still be extended, and is known as the Legendre-Fenchel transformation. In this more general setting, a few properties are lost: for example, the Legendre transform is no longer its own inverse (unless there are extra assumptions, like convexity).

Legendre transformation on manifolds

Let $M$ be a smooth manifold, and let $TM$ denote its tangent bundle. Let $L : TM \to R$ be a smooth function, which we will refer to as the Lagrangian. The Legendre transformation of $L$ is a morphism of vector bundles $F L : TM \to T * M$ defined as follows. Suppose that $n = dim M$ and that $U \subseteq M$ is a chart. Then $U \times R n$ is a chart on $TM$ , and for any point $(x, v)$ in this chart, the Legendre transformation of $L$ is defined by

\mathbf {F} L(x,v)=\left(x,{\frac {\partial L}{\partial v}}(x,v)\right).

The associated energy function is the function $E : TM \to R$ defined by

E(x,v)=\langle v,\mathbf {F} L(x,v)\rangle -L(x,v),

where the angle brackets denote the natural pairing of a tangent and cotangent vector. The Legendre transform can be further generalized to a function from a vector bundle over $M$ to its dual bundle.[2]

Further properties

Scaling properties

The Legendre transformation has the following scaling properties: For $a > 0$ ,

f(x)=a\cdot g(x)\Rightarrow f^{\star }(p)=a\cdot g^{\star }\left({\frac {p}{a}}\right)

f(x)=g(a\cdot x)\Rightarrow f^{\star }(p)=g^{\star }\left({\frac {p}{a}}\right).

It follows that if a function is homogeneous of degree $r$ then its image under the Legendre transformation is a homogeneous function of degree $s$ , where $1/ r + 1/ s = 1$ . (Since $f (x) = x r / r$ , with $r > 1$ , implies $f *(p) = p s / s$ .) Thus, the only monomial whose degree is invariant under Legendre transform is the quadratic.

Behavior under translation

f(x)=g(x)+b\Rightarrow f^{\star }(p)=g^{\star }(p)-b

f(x)=g(x+y)\Rightarrow f^{\star }(p)=g^{\star }(p)-p\cdot y

Behavior under inversion

f(x)=g^{-1}(x)\Rightarrow f^{\star }(p)=-p\cdot g^{\star }\left({\frac {1}{p}}\right)

Behavior under linear transformations

Let $A : R n \to R m$ be a linear transformation. For any convex function $f$ on $R n$ , one has

(Af)^{\star }=f^{\star }A^{\star }

where $A *$ is the adjoint operator of $A$ defined by

\left\langle Ax,y^{\star }\right\rangle =\left\langle x,A^{\star }y^{\star }\right\rangle ,

and $Af$ is the push-forward of $f$ along $A$

(Af)(y)=\inf\{f(x):x\in X,Ax=y\}.

A closed convex function $f$ is symmetric with respect to a given set $G$ of orthogonal linear transformations,

f(Ax)=f(x),\;\forall x,\;\forall A\in G

if and only if $f *$ is symmetric with respect to $G$ .

Infimal convolution

The infimal convolution of two functions $f$ and $g$ is defined as

\left(f\star _{\inf }g\right)(x)=\inf \left\{f(x-y)+g(y)\,|\,y\in \mathbf {R} ^{n}\right\}.

Let $f 1, ..., f m$ be proper convex functions on $R n$ . Then

\left(f_{1}\star _{\inf }\cdots \star _{\inf }f_{m}\right)^{\star }=f_{1}^{\star }+\cdots +f_{m}^{\star }.

Fenchel's inequality

For any function $f$ and its convex conjugate $f *$ Fenchel's inequality (also known as the Fenchel–Young inequality) holds for every $x \in X$ and $p \in X *$ , i.e., independent $x, p$ pairs,

\left\langle p,x\right\rangle \leq f(x)+f^{\star }(p).

References

"Archived copy". Archived from the original on 2015-03-12. Retrieved 2011-01-26.CS1 maint: archived copy as title (link)
Marsden, Jerrod E., and Ratiu, Tudor, Introduction to Mechanics and Symmetry: A Basic Exposition of Classical Mechanical Systems, Springer-Verlag, 1999, ISBN 978-0-387-98643-2, doi 10.1007/978-0-387-21792-5.

Courant, Richard; Hilbert, David (2008). Methods of Mathematical Physics. 2. John Wiley & Sons. ISBN 978-0471504399.
Arnol'd, Vladimir Igorevich (1989). Mathematical Methods of Classical Mechanics (2nd ed.). Springer. ISBN 0-387-96890-3.
Fenchel, W. (1949). "On conjugate convex functions", Can. J. Math 1: 73-77.
Rockafellar, R. Tyrrell (1996) [1970]. Convex Analysis. Princeton University Press. ISBN 0-691-01586-4.
Zia, R. K. P.; Redish, E. F.; McKay, S. R. (2009). "Making sense of the Legendre transform". American Journal of Physics. 77 (7): 614. arXiv:0806.1147. Bibcode:2009AmJPh..77..614Z. doi:10.1119/1.3119512.

External links

Legendre transform with figures at maze5.net
Legendre and Legendre-Fenchel transforms in a step-by-step explanation at onmyphd.com

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] "Archived copy". Archived from the original on 2015-03-12. Retrieved 2011-01-26.CS1 maint: archived copy as title (link)

[2] Marsden, Jerrod E., and Ratiu, Tudor, Introduction to Mechanics and Symmetry: A Basic Exposition of Classical Mechanical Systems, Springer-Verlag, 1999, ISBN 978-0-387-98643-2, doi 10.1007/978-0-387-21792-5.

Legendre transformation

Definition

Understanding the transform in terms of derivatives

Properties

Examples

Example 1

Example 2

Example 3

Example 4

Example 5: several variables

Behavior of differentials under Legendre transforms

Applications

Analytical mechanics

Thermodynamics

An example – variable capacitor

Probability theory

Microeconomics

Geometric interpretation

Legendre transformation in more than one dimension

Legendre transformation on manifolds

Further properties

Scaling properties

Behavior under translation

Behavior under inversion

Behavior under linear transformations

Infimal convolution

Fenchel's inequality

See also

References

Further reading

External links