List of pitch intervals

Below is a list of intervals expressible in terms of a prime limit (see Terminology), completed by a choice of intervals in various equal subdivisions of the octave or of other intervals.

Comparison between tunings: Pythagorean, equal-tempered, quarter-comma meantone, and others. For each, the common origin is arbitrarily chosen as C. The degrees are arranged in the order or the cycle of fifths; as in each of these tunings except just intonation all fifths are of the same size, the tunings appear as straight lines, the slope indicating the relative tempering with respect to Pythagorean, which has pure fifths (3:2, 702 cents). The Pythagorean A♭ (at the left) is at 792 cents, G♯ (at the right) at 816 cents; the difference is the Pythagorean comma. Equal temperament by definition is such that A♭ and G♯ are at the same level. ​1⁄4-comma meantone produces the "just" major third (5:4, 386 cents, a syntonic comma lower than the Pythagorean one of 408 cents). ​1⁄3-comma meantone produces the "just" minor third (6:5, 316 cents, a syntonic comma higher than the Pythagorean one of 294 cents). In both these meantone temperaments, the enharmony, here the difference between A♭ and G♯, is much larger than in Pythagorean, and with the flat degree higher than the sharp one.
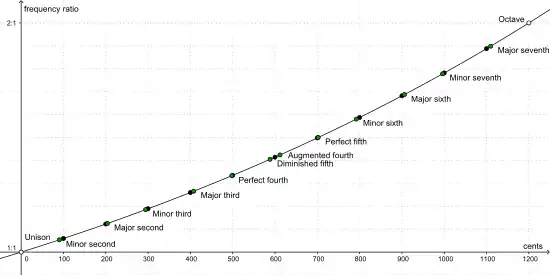
Comparison of two sets of musical intervals. The equal-tempered intervals are black; the Pythagorean intervals are green.

For commonly encountered harmonic or melodic intervals between pairs of notes in contemporary Western music theory, without consideration of the way in which they are tuned, see Interval (music) § Main intervals.

Terminology
  • The prime limit[1] henceforth referred to simply as the limit, is the largest prime number occurring in the factorizations of the numerator and denominator of the frequency ratio describing a rational interval. For instance, the limit of the just perfect fourth (4:3) is 3, but the just minor tone (10:9) has a limit of 5, because 10 can be factored into 2 × 5 (and 9 into 3 × 3). There exists another type of limit, the odd limit, a concept used by Harry Partch (bigger of odd numbers obtained after dividing numerator and denominator by highest possible powers of 2), but it is not used here. The term "limit" was devised by Partch.[1]
  • By definition, every interval in a given limit can also be part of a limit of higher order. For instance, a 3-limit unit can also be part of a 5-limit tuning and so on. By sorting the limit columns in the table below, all intervals of a given limit can be brought together (sort backwards by clicking the button twice).
  • Pythagorean tuning means 3-limit intonation—a ratio of numbers with prime factors no higher than three.
  • Just intonation means 5-limit intonation—a ratio of numbers with prime factors no higher than five.
  • Septimal, undecimal, tridecimal, and septendecimal mean, respectively, 7, 11, 13, and 17-limit intonation.
  • Meantone refers to meantone temperament, where the whole tone is the mean of the major third. In general, a meantone is constructed in the same way as Pythagorean tuning, as a stack of fifths: the tone is reached after two fifths, the major third after four, so that as all fifths are the same, the tone is the mean of the third. In a meantone temperament, each fifth is narrowed ("tempered") by the same small amount. The most common of meantone temperaments is the quarter-comma meantone, in which each fifth is tempered by ​1⁄4 of the syntonic comma, so that after four steps the major third (as C-G-D-A-E) is a full syntonic comma lower than the Pythagorean one. The extremes of the meantone systems encountered in historical practice are the Pythagorean tuning, where the whole tone corresponds to 9:8, i.e. (3:2)2/2, the mean of the major third (3:2)4/4, and the fifth (3:2) is not tempered; and the ​1⁄3-comma meantone, where the fifth is tempered to the extent that three ascending fifths produce a pure minor third.(See Meantone temperaments). The music program Logic Pro uses also ​1⁄2-comma meantone temperament.
  • Equal-tempered refers to X-tone equal temperament with intervals corresponding to X divisions per octave.
  • Tempered intervals however cannot be expressed in terms of prime limits and, unless exceptions, are not found in the table below.
  • The table can also be sorted by frequency ratio, by cents, or alphabetically.
  • Superparticular ratios are intervals that can be expressed as the ratio of two consecutive integers.

List
ColumnLegend
TETX-tone equal temperament (12-tet, etc.).
Limit3-limit intonation, or Pythagorean.
5-limit "just" intonation, or just.
7-limit intonation, or septimal.
11-limit intonation, or undecimal.
13-limit intonation, or tridecimal.
17-limit intonation, or septendecimal.
19-limit intonation, or novendecimal.
Higher limits.
MMeantone temperament or tuning.
SSuperparticular ratio (no separate color code).
List of musical intervals
CentsNote (from C)Freq. ratioPrime factorsInterval nameTETLimitMS
0.00C[2]1 : 11 : 1play Unison,[3] monophony,[4] perfect prime,[3] tonic,[5] or fundamental1, 123M
0.03 65537 : 6553665537 : 216play Sixty-five-thousand-five-hundred-thirty-seventh harmonic 65537S
0.40C♯−4375 : 437454×7 : 2×37play Ragisma[3][6]7S
0.72E+2401 : 240074 : 25×3×52play Breedsma[3][6]7S
1.00 21/120021/1200play Cent[7]1200
1.20 21/100021/1000play Millioctave1000
1.95 B♯++32805 : 3276838×5 : 215play Schisma[3][5]5
1.96 3:2÷(27/12)3 : 219/12Grad, Werckmeister[8]
3.99 101/100021/1000×51/1000play Savart or eptaméride301.03
7.71 B♯225 : 22432×52 : 25×7play Septimal kleisma,[3][6] marvel comma7S
8.11 B−15625 : 1555256 : 26×35play Kleisma or semicomma majeur[3][6]5
10.06 A++2109375 : 209715233×57 : 221play Semicomma,[3][6] Fokker's comma[3]5
10.85 C160 : 15925×5 : 3×53play Difference between 5:3 & 53:3253S
11.98C145 : 1445×29 : 24×32play Difference between 29:16 & 9:529S
12.50 21/9621/96play Sixteenth tone96
13.07B−1728 : 171526×33 : 5×73play Orwell comma[3][9]7
13.47C129 : 1283×43 : 27play Hundred-twenty-ninth harmonic43S
13.79 D126 : 1252×32×7 : 53play Small septimal semicomma,[6] small septimal comma,[3] starling comma7S
14.37 C♭↑↑−121 : 120112 : 23×3×5play Undecimal seconds comma[3]11S
16.67 C↑[lower-alpha 1]21/7221/72play 1 step in 72 equal temperament72
18.13 C96 : 9525×3 : 5×19play Difference between 19:16 & 6:519S
19.55 D--[2]2048 : 2025211 : 34×52play Diaschisma,[3][6] minor comma5
21.51 C+[2]81 : 8034 : 24×5play Syntonic comma,[3][5][6] major comma, komma, chromatic diesis, or comma of Didymus[3][6][10][11]5S
22.64 21/5321/53play Holdrian comma, Holder's comma, 1 step in 53 equal temperament53
23.46 B♯+++531441 : 524288312 : 219play Pythagorean comma,[3][5][6][10][11] ditonic comma[3][6]3
25.00 21/4821/48play Eighth tone48
26.84 C65 : 645×13 : 26play Sixty-fifth harmonic,[5] 13th-partial chroma[3]13S
27.26 C−64 : 6326 : 32×7play Septimal comma,[3][6][11] Archytas' comma,[3] 63rd subharmonic7S
29.2721/4121/41play 1 step in 41 equal temperament41
31.19 D♭↓56 : 5523×7 : 5×11play Undecimal diesis,[3] Ptolemy's enharmonic:[5] difference between (11 : 8) and (7 : 5) tritone11S
33.33C/D♭[lower-alpha 1]21/3621/36play Sixth tone36, 72
34.28 C51 : 503×17 : 2×52play Difference between 17:16 & 25:2417S
34.98 B♯-50 : 492×52 : 72play Septimal sixth tone or jubilisma, Erlich's decatonic comma or tritonic diesis[3][6]7S
35.70 D♭49 : 4872 : 24×3play Septimal diesis, slendro diesis or septimal 1/6-tone[3]7S
38.05 C46 : 452×23 : 32×5play Inferior quarter tone,[5] difference between 23:16 & 45:3223S
38.71 21/3121/31play 1 step in 31 equal temperament31
38.91 C↓♯+45 : 4432×5 : 4×11play Undecimal diesis or undecimal fifth tone 11S
40.00 21/3021/30play Fifth tone30
41.06 D−128 : 12527 : 53play Enharmonic diesis or 5-limit limma, minor diesis,[6] diminished second,[5][6] minor diesis or diesis,[3] 125th subharmonic5
41.72 D♭42 : 412×3×7 : 41play Lesser 41-limit fifth tone41S
42.75 C41 : 4041 : 23×5play Greater 41-limit fifth tone41S
43.83 C♯40 : 3923×5 : 3×13play Tridecimal fifth tone13S
44.97 C39 : 383×13 : 2×19play Superior quarter-tone,[5] novendecimal fifth tone19S
46.17 D-38 : 372×19 : 37play Lesser 37-limit quarter tone37S
47.43 C♯37 : 3637 : 22×32play Greater 37-limit quarter tone37S
48.77 C36 : 3522×32 : 5×7play Septimal quarter tone, septimal diesis,[3][6] septimal chroma,[2] superior quarter tone[5]7S
49.98 246 : 2393×41 : 239play Just quarter tone[11]239
50.00 C/D21/2421/24play Equal-tempered quarter tone24
50.18 D♭35 : 345×7 : 2×17play ET quarter-tone approximation,[5] lesser 17-limit quarter tone17S
50.72 B♯++59049 : 57344310 : 213×7play Harrison's comma (10 P5s - 1 H7)[3]7
51.68 C↓♯34 : 332×17 : 3×11play Greater 17-limit quarter tone17S
53.27 C↑33 : 323×11 : 25play Thirty-third harmonic,[5] undecimal comma, undecimal quarter tone11S
54.96 D♭-32 : 3125 : 31play Inferior quarter-tone,[5] thirty-first subharmonic31S
56.55 B♯+529 : 512232 : 29play Five-hundred-twenty-ninth harmonic23
56.77 C31 : 3031 : 2×3×5play Greater quarter-tone,[5] difference between 31:16 & 15:831S
58.69 C♯30 : 292×3×5 : 29play Lesser 29-limit quarter tone29S
60.75 C29 : 2829 : 22×7play Greater 29-limit quarter tone29S
62.96 D♭-28 : 2722×7 : 33play Septimal minor second, small minor second, inferior quarter tone[5]7S
63.81 (3 : 2)1/1131/11 : 21/11play Beta scale step18.75
65.34 C♯+27 : 2633 : 2×13 play Chromatic diesis,[12] tridecimal comma[3]13S
66.34 D♭133 : 1287×19 : 27play One-hundred-thirty-third harmonic19
66.67 C↑/C♯[lower-alpha 1]21/1821/18play Third tone18, 36, 72
67.90 D-26 : 252×13 : 52play Tridecimal third tone, third tone[5]13S
70.67 C♯[2]25 : 2452 : 23×3play Just chromatic semitone or minor chroma,[3] lesser chromatic semitone, small (just) semitone[11] or minor second,[4] minor chromatic semitone,[13] or minor semitone,[5] ​2⁄7-comma meantone chromatic semitone, augmented unison5S
73.68 D♭-24 : 2323×3 : 23play Lesser 23-limit semitone23S
75.00 21/1623/48play 1 step in 16 equal temperament, 3 steps in 4816, 48
76.96 C↓♯+23 : 2223 : 2×11play Greater 23-limit semitone23S
78.00 (3 : 2)1/931/9 : 21/9play Alpha scale step15.39
79.31 67 : 6467 : 26play Sixty-seventh harmonic[5]67
80.54 C↑-22 : 212×11 : 3×7play Hard semitone,[5] two-fifth tone small semitone11S
84.47 D♭21 : 203×7 : 22×5play Septimal chromatic semitone, minor semitone[3]7S
88.80 C♯20 : 1922×5 : 19play Novendecimal augmented unison19S
90.22 D♭−−[2]256 : 24328 : 35play Pythagorean minor second or limma,[3][6][11] Pythagorean diatonic semitone, Low Semitone[14]3
92.18 C♯+[2]135 : 12833×5 : 27play Greater chromatic semitone, chromatic semitone, semitone medius, major chroma or major limma,[3] small limma,[11] major chromatic semitone,[13] limma ascendant[5]5
93.60 D♭-19 : 1819 : 2×9Novendecimal minor secondplay 19S
97.36 D↓↓128 : 12127 : 112play 121st subharmonic,[5][6] undecimal minor second11
98.95 D♭18 : 172×32 : 17play Just minor semitone, Arabic lute index finger[3]17S
100.00 C♯/D♭21/1221/12play Equal-tempered minor second or semitone12M
104.96 C♯[2]17 : 1617 : 24play Minor diatonic semitone, just major semitone, overtone semitone,[5] 17th harmonic,[3] limma17S
111.45 25√5(5 : 1)1/25play Studie II interval (compound just major third, 5:1, divided into 25 equal parts)25
111.73 D♭-[2]16 : 1524 : 3×5play Just minor second,[15] just diatonic semitone, large just semitone or major second,[4] major semitone,[5] limma, minor diatonic semitone,[3] diatonic second[16] semitone,[14] diatonic semitone,[11] ​1⁄6-comma meantone minor second5S
113.69 C♯++2187 : 204837 : 211play Apotome[3][11] or Pythagorean major semitone,[6] Pythagorean augmented unison, Pythagorean chromatic semitone, or Pythagorean apotome3
116.72 (18 : 5)1/1921/19×32/19 : 51/19play Secor10.28
119.44 C♯15 : 143×5 : 2×7play Septimal diatonic semitone, major diatonic semitone,[3] Cowell semitone[5]7S
125.00 25/4825/48play 5 steps in 48 equal temperament48
128.30 D14 : 132×7 : 13play Lesser tridecimal 2/3-tone[17]13S
130.23 C♯+69 : 643×23 : 26play Sixty-ninth harmonic[5]23
133.24 D♭27 : 2533 : 52play Semitone maximus, minor second, large limma or Bohlen-Pierce small semitone,[3] high semitone,[14] alternate Renaissance half-step,[5] large limma, acute minor second5
133.33 C♯/D♭[lower-alpha 1]21/922/18play Two-third tone9, 18, 36, 72
138.57 D♭-13 : 1213 : 22×3play Greater tridecimal 2/3-tone,[17] Three-quarter tone[5]13S
150.00 C/D23/2421/8play Equal-tempered neutral second8, 24
150.64 D↓[2]12 : 1122×3 : 11play ​3⁄4 tone or Undecimal neutral second,[3][5] trumpet three-quarter tone,[11] middle finger [between frets][14]11S
155.14 D35 : 325×7 : 25play Thirty-fifth harmonic[5]7
160.90 D−−800 : 72925×52 : 36play Grave whole tone,[3] neutral second, grave major second5
165.00 D↑♭−[2]11 : 1011 : 2×5play Greater undecimal minor/major/neutral second, 4/5-tone[6] or Ptolemy's second[3]11S
171.43 21/721/7play 1 step in 7 equal temperament7
175.00 27/4827/48play 7 steps in 48 equal temperament48
179.70 71 : 6471 : 26play Seventy-first harmonic[5]71
180.45 E−−−65536 : 59049216 : 310play Pythagorean diminished third,[3][6] Pythagorean minor tone3
182.40 D-[2]10 : 92×5 : 32play Small just whole tone or major second,[4] minor whole tone,[3][5] lesser whole tone,[16] minor tone,[14] minor second,[11] half-comma meantone major second5S
200.00 D22/1221/6play Equal-tempered major second6, 12M
203.91 D[2]9 : 832 : 23play Pythagorean major second, Large just whole tone or major second[11] (sesquioctavan),[4] tonus, major whole tone,[3][5] greater whole tone,[16] major tone[14]3S
215.89 D145 : 1285×29 : 27play Hundred-forty-fifth harmonic29
223.46 E−[2]256 : 22528 : 32×52play Just diminished third,[16] 225th subharmonic5
225.00 23/1629/48play 9 steps in 48 equal temperament16, 48
227.79 73 : 6473 : 26play Seventy-third harmonic[5]73
231.17 D−[2]8 : 723 : 7play Septimal major second,[4] septimal whole tone[3][5]7S
240.00 21/521/5play 1 step in 5 equal temperament5
247.74 D♯15 : 133×5 : 13play Tridecimal ​5⁄4 tone[3]13
250.00 D/E25/2425/24play 5 steps in 24 equal temperament24
251.34 D♯37 : 3237 : 25play Thirty-seventh harmonic[5]37
253.08 D♯−125 : 10853 : 22×33play Semi-augmented whole tone,[3] semi-augmented second5
262.37 E↓♭64 : 5526 : 5×11play 55th subharmonic[5][6]11
268.80 D299 : 25613×23 : 28play Two-hundred-ninety-ninth harmonic23
266.87 E♭[2]7 : 67 : 2×3play Septimal minor third[3][4][11] or Sub minor third[14]7S
274.58 D♯[2]75 : 643×52 : 26play Just augmented second,[16] Augmented tone,[14] augmented second[5][13]5
275.00 211/48211/48play 11 steps in 48 equal temperament48
289.21 E↓♭13 : 1113 : 11play Tridecimal minor third[3]13
294.13 E♭−[2]32 : 2725 : 33play Pythagorean minor third[3][5][6][14][16] semiditone, or 27th subharmonic3
297.51 E♭[2]19 : 1619 : 24play 19th harmonic,[3] 19-limit minor third, overtone minor third[5]19
300.00 D♯/E♭23/1221/4play Equal-tempered minor third4, 12M
301.85 D♯-25 : 21[5]52 : 3×7play Quasi-equal-tempered minor third, 2nd 7-limit minor third, Bohlen-Pierce second[3][6]7
310.26 6:5÷(81:80)1/422 : 53/4play Quarter-comma meantone minor thirdM
311.98 (3 : 2)4/934/9 : 24/9play Alpha scale minor third3.85
315.64 E♭[2]6 : 52×3 : 5play Just minor third,[3][4][5][11][16] minor third,[14] ​1⁄3-comma meantone minor third5MS
317.60 D♯++19683 : 1638439 : 214play Pythagorean augmented second[3][6]3
320.14 E♭↑77 : 647×11 : 26play Seventy-seventh harmonic[5]11
325.00 213/48213/48play 13 steps in 48 equal temperament48
336.13 D♯-17 : 1417 : 2×7play Superminor third[18]17
337.15 E♭+243 : 20035 : 23×52play Acute minor third[3]5
342.48 E♭39 : 323×13 : 25play Thirty-ninth harmonic[5]13
342.86 22/722/7play 2 steps in 7 equal temperament7
342.91 E♭-128 : 10527 : 3×5×7play 105th subharmonic,[5] septimal neutral third[6]7
347.41 E↑♭−[2]11 : 911 : 32play Undecimal neutral third[3][5]11
350.00 D/E27/2427/24play Equal-tempered neutral third24
354.55 E↓+27 : 2233 : 2×11play Zalzal's wosta[6] 12:11 X 9:8[14]11
359.47 E[2]16 : 1324 : 13play Tridecimal neutral third[3]13
364.54 79 : 6479 : 26play Seventy-ninth harmonic[5]79
364.81 E−100 : 8122×52 : 34play Grave major third[3]5
375.00 25/16215/48play 15 steps in 48 equal temperament16, 48
384.36 F♭−−8192 : 6561213 : 38play Pythagorean diminished fourth,[3][6] Pythagorean 'schismatic' third[5]3
386.31 E[2]5 : 45 : 22play Just major third,[3][4][5][11][16] major third,[14] quarter-comma meantone major third5MS
397.10 E+161 : 1287×23 : 27play One-hundred-sixty-first harmonic23
400.00 E24/1221/3play Equal-tempered major third3, 12M
402.47 E323 : 25617×19 : 28play Three-hundred-twenty-third harmonic19
407.82 E+[2]81 : 6434 : 26play Pythagorean major third,[3][5][6][14][16] ditone3
417.51 F↓+[2]14 : 112×7 : 11play Undecimal diminished fourth or major third[3]11
425.00 217/48217/48play 17 steps in 48 equal temperament48
427.37 F♭[2]32 : 2525 : 52play Just diminished fourth,[16] diminished fourth,[5][13] 25th subharmonic5
429.06 E41 : 3241 : 25play Forty-first harmonic[5]41
435.08 E[2]9 : 732 : 7play Septimal major third,[3][5] Bohlen-Pierce third,[3] Super major Third[14]7
444.77 F↓128 : 9927 : 9×11play 99th subharmonic[5][6]11
450.00 E/F29/2429/24play 9 steps in 24 equal temperament24
450.05 83 : 6483 : 26play Eighty-third harmonic[5]83
454.21 F♭13 : 1013 : 2×5play Tridecimal major third or diminished fourth13
456.99 E♯[2]125 : 9653 : 25×3play Just augmented third, augmented third[5]5
462.35 E-64 : 4926 : 72play 49th subharmonic[5][6]7
470.78 F+[2]21 : 163×7 : 24play Twenty-first harmonic, narrow fourth,[3] septimal fourth,[5] wide augmented third, H7 on G7
475.00 219/48219/48play 19 steps in 48 equal temperament48
478.49 E♯+675 : 51233×52 : 29play Six-hundred-seventy-fifth harmonic, wide augmented third[3]5
480.00 22/522/5play 2 steps in 5 equal temperament5
491.27 E♯85 : 645×17 : 26play Eighty-fifth harmonic[5]17
498.04 F[2]4 : 322 : 3play Perfect fourth,[3][5][16] Pythagorean perfect fourth, Just perfect fourth or diatessaron[4]3S
500.00 F25/1225/12play Equal-tempered perfect fourth12M
501.42 F+171 : 12832×19 : 27play One-hundred-seventy-first harmonic19
510.51 (3 : 2)8/1138/11 : 28/11play Beta scale perfect fourth18.75
511.52 F43 : 3243 : 25play Forty-third harmonic[5]43
514.29 23/723/7play 3 steps in 7 equal temperament7
519.55 F+[2]27 : 2033 : 22×5play 5-limit wolf fourth, acute fourth,[3] imperfect fourth[16]5
521.51 E♯+++177147 : 131072311 : 217play Pythagorean augmented third[3][6] (F+ (pitch))3
525.00 27/16221/48play 21 steps in 48 equal temperament16, 48
531.53 F+87 : 643×29 : 26play Eighty-seventh harmonic[5]29
536.95 F↓♯+15 : 113×5 : 11play Undecimal augmented fourth[3]11
550.00 F/G211/24211/24play 11 steps in 24 equal temperament24
551.32 F↑[2]11 : 811 : 23play eleventh harmonic,[5] undecimal tritone,[5] lesser undecimal tritone, undecimal semi-augmented fourth[3]11
563.38 F♯+18 : 132×9 : 13play Tridecimal augmented fourth[3]13
568.72 F♯[2]25 : 1852 : 2×32play Just augmented fourth[3][5]5
570.88 89 : 6489 : 26play Eighty-ninth harmonic[5]89
575.00 223/48223/48play 23 steps in 48 equal temperament48
582.51 G♭[2]7 : 57 : 5play Lesser septimal tritone, septimal tritone[3][4][5] Huygens' tritone or Bohlen-Pierce fourth,[3] septimal fifth,[11] septimal diminished fifth[19]7
588.27 G♭−−1024 : 729210 : 36play Pythagorean diminished fifth,[3][6] low Pythagorean tritone[5]3
590.22 F♯+[2]45 : 3232×5 : 25play Just augmented fourth, just tritone,[4][11] tritone,[6] diatonic tritone,[3] 'augmented' or 'false' fourth,[16] high 5-limit tritone,[5] ​1⁄6-comma meantone augmented fourth5
595.03 G♭361 : 256192 : 28play Three-hundred-sixty-first harmonic19
600.00 F♯/G♭26/1221/2=√2play Equal-tempered tritone2, 12M
609.35 G♭91 : 647×13 : 26play Ninety-first harmonic[5]13
609.78 G♭−[2]64 : 4526 : 32×5play Just tritone,[4] 2nd tritone,[6] 'false' fifth,[16] diminished fifth,[13] low 5-limit tritone,[5] 45th subharmonic5
611.73 F♯++729 : 51236 : 29play Pythagorean tritone,[3][6] Pythagorean augmented fourth, high Pythagorean tritone[5]3
617.49 F♯[2]10 : 72×5 : 7play Greater septimal tritone, septimal tritone,[4][5] Euler's tritone[3]7
625.00 225/48225/48play 25 steps in 48 equal temperament48
628.27 F♯+23 : 1623 : 24play Twenty-third harmonic,[5] classic diminished fifth23
631.28 G♭[2]36 : 2522×32 : 52play Just diminished fifth[5]5
646.99 F♯+93 : 643×31 : 26play Ninety-third harmonic[5]31
648.68 G↓[2]16 : 1124 : 11play ` undecimal semi-diminished fifth[3]11
650.00 F/G213/24213/24play 13 steps in 24 equal temperament24
665.51 G47 : 3247 : 25play Forty-seventh harmonic[5]47
675.00 29/16227/48play 27 steps in 48 equal temperament16, 48
678.49 A−−−262144 : 177147218 : 311play Pythagorean diminished sixth[3][6]3
680.45 G−40 : 2723×5 : 33play 5-limit wolf fifth,[5] or diminished sixth, grave fifth,[3][6][11] imperfect fifth,[16]5
683.83 G95 : 645×19 : 26play Ninety-fifth harmonic[5]19
684.82 E++12167 : 8192233 : 213play 12167th harmonic23
685.71 24/7 : 1play 4 steps in 7 equal temperament
691.20 3:2÷(81:80)1/22×51/2 : 3play Half-comma meantone perfect fifthM
694.79 3:2÷(81:80)1/321/3×51/3 : 31/3play ​1⁄3-comma meantone perfect fifthM
695.81 3:2÷(81:80)2/721/7×52/7 : 31/7play ​2⁄7-comma meantone perfect fifthM
696.58 3:2÷(81:80)1/451/4play Quarter-comma meantone perfect fifthM
697.65 3:2÷(81:80)1/531/5×51/5 : 21/5play ​1⁄5-comma meantone perfect fifthM
698.37 3:2÷(81:80)1/631/3×51/6 : 21/3play ​1⁄6-comma meantone perfect fifthM
700.00 G27/1227/12play Equal-tempered perfect fifth12M
701.89 231/53231/53play 53-TET perfect fifth53
701.96 G[2]3 : 23 : 2play Perfect fifth,[3][5][16] Pythagorean perfect fifth, Just perfect fifth or diapente,[4] fifth,[14] Just fifth[11]3S
702.44 224/41224/41play 41-TET perfect fifth41
703.45 217/29217/29play 29-TET perfect fifth29
719.90 97 : 6497 : 26play Ninety-seventh harmonic[5]97
720.00 23/5 : 1play 3 steps in 5 equal temperament5
721.51 A−1024 : 675210 : 33×52play Narrow diminished sixth[3]5
725.00 229/48229/48play 29 steps in 48 equal temperament48
729.22 G-32 : 2124 : 3×7play 21st subharmonic,[5][6] septimal diminished sixth7
733.23 F+391 : 25617×23 : 28play Three-hundred-ninety-first harmonic23
737.65 A♭+49 : 327×7 : 25play Forty-ninth harmonic[5]7
743.01 A192 : 12526×3 : 53play Classic diminished sixth[3]5
750.00 G/A215/24215/24play 15 steps in 24 equal temperament24
755.23 G↑99 : 6432×11 : 26play Ninety-ninth harmonic[5]11
764.92 A♭[2]14 : 92×7 : 32play Septimal minor sixth[3][5]7
772.63 G♯25 : 1652 : 24play Just augmented fifth[5][16]
775.00 231/48231/48play 31 steps in 48 equal temperament48
781.79 π : 2play Wallis product
782.49 G↑-[2]11 : 711 : 7play Undecimal minor sixth,[5] undecimal augmented fifth,[3] Fibonacci numbers11
789.85 101 : 64101 : 26play Hundred-first harmonic[5]101
792.18 A♭−[2]128 : 8127 : 34play Pythagorean minor sixth,[3][5][6] 81st subharmonic3
798.40 A♭+203 : 1287×29 : 27play Two-hundred-third harmonic29
800.00 G♯/A♭28/1222/3play Equal-tempered minor sixth3, 12M
806.91 G♯51 : 323×17 : 25play Fifty-first harmonic[5]17
813.69 A♭[2]8 : 523 : 5play Just minor sixth[3][4][11][16]5
815.64 G♯++6561 : 409638 : 212play Pythagorean augmented fifth,[3][6] Pythagorean 'schismatic' sixth[5]3
823.80 103 : 64103 : 26play Hundred-third harmonic[5]103
825.00 211/16233/48play 33 steps in 48 equal temperament16, 48
832.18 G♯+207 : 12832×23 : 27play Two-hundred-seventh harmonic23
833.09 51/2+1 : 2φ : 1play Golden ratio (833 cents scale)
833.11 233 : 144233 : 24×32play Golden ratio approximation (833 cents scale) 233
835.19 A♭+81 : 5034 : 2×52play Acute minor sixth[3]5
840.53 A♭[2]13 : 813 : 23play Tridecimal neutral sixth,[3] overtone sixth,[5] thirteenth harmonic13
848.83 A♭↑209 : 12811×19 : 27play Two-hundred-ninth harmonic19
850.00 G/A217/24217/24play Equal-tempered neutral sixth24
852.59 A↓+[2]18 : 112×32 : 11play Undecimal neutral sixth,[3][5] Zalzal's neutral sixth11
857.09 A+105 : 643×5×7 : 26play Hundred-fifth harmonic[5]7
857.14 25/725/7play 5 steps in 7 equal temperament7
862.85 A−400 : 24324×52 : 35play Grave major sixth[3]5
873.50 A53 : 3253 : 25play Fifty-third harmonic[5]53
875.00 235/48235/48play 35 steps in 48 equal temperament48
879.86 A↓128 : 7727 : 7×11play 77th subharmonic[5][6]11
882.40 B−−−32768 : 19683215 : 39play Pythagorean diminished seventh[3][6]3
884.36 A[2]5 : 35 : 3play Just major sixth,[3][4][5][11][16] Bohlen-Pierce sixth,[3] ​1⁄3-comma meantone major sixth5M
889.76 107 : 64107 : 26play Hundred-seventh harmonic[5]107
892.54 B6859 : 4096193 : 212play 6859th harmonic19
900.00 A29/1223/4play Equal-tempered major sixth4, 12M
902.49 A32 : 1925 : 19play 19th subharmonic[5][6]19
905.87 A+[2]27 : 1633 : 24play Pythagorean major sixth[3][5][11][16]3
921.82 109 : 64109 : 26play Hundred-ninth harmonic[5]109
925.00 237/48237/48play 37 steps in 48 equal temperament48
925.42 B−[2]128 : 7527 : 3×52play Just diminished seventh,[16] diminished seventh,[5][13] 75th subharmonic5
925.79 A+437 : 25619×23 : 28play Four-hundred-thirty-seventh harmonic23
933.13 A[2]12 : 722×3 : 7play Septimal major sixth[3][4][5]7
937.63 A↑55 : 325×11 : 25play Fifty-fifth harmonic[5][20]11
950.00 A/B219/24219/24play 19 steps in 24 equal temperament24
953.30 A♯+111 : 643×37 : 26play Hundred-eleventh harmonic[5]37
955.03 A♯[2]125 : 7253 : 23×32play Just augmented sixth[5]5
957.21 (3 : 2)15/11315/11 : 215/11play 15 steps in Beta scale18.75
960.00 24/524/5play 4 steps in 5 equal temperament5
968.83 B♭[2]7 : 47 : 22play Septimal minor seventh,[4][5][11] harmonic seventh,[3][11] augmented sixth7
975.00 213/16239/48play 39 steps in 48 equal temperament16, 48
976.54 A♯+[2]225 : 12832×52 : 27play Just augmented sixth[16]5
984.21 113 : 64113 : 26play Hundred-thirteenth harmonic[5]113
996.09B♭−[2]16 : 924 : 32play Pythagorean minor seventh,[3] Small just minor seventh,[4] lesser minor seventh,[16] just minor seventh,[11] Pythagorean small minor seventh[5]3
999.47 B♭57 : 323×19 : 25play Fifty-seventh harmonic[5]19
1000.00A♯/B♭210/1225/6play Equal-tempered minor seventh6, 12M
1014.59 A♯+115 : 645×23 : 26play Hundred-fifteenth harmonic[5]23
1017.60B♭[2]9 : 532 : 5play Greater just minor seventh,[16] large just minor seventh,[4][5] Bohlen-Pierce seventh[3]5
1019.55 A♯+++59049 : 32768310 : 215play Pythagorean augmented sixth[3][6]3
1025.00 241/48241/48play 41 steps in 48 equal temperament48
1028.57 26/726/7play 6 steps in 7 equal temperament7
1029.58 B♭29 : 1629 : 24play Twenty-ninth harmonic,[5] minor seventh29
1035.00B↓[2]20 : 1122×5 : 11play Lesser undecimal neutral seventh, large minor seventh[3]11
1039.10 B♭+729 : 40036 : 24×52play Acute minor seventh[3]5
1044.44 B♭117 : 6432×13 : 26play Hundred-seventeenth harmonic[5]13
1044.86 B♭-64 : 3526 : 5×7play 35th subharmonic,[5] septimal neutral seventh[6]7
1049.36B↑♭−[2]11 : 611 : 2×3play ​21⁄4-tone or Undecimal neutral seventh,[3] undecimal 'median' seventh[5]11
1050.00 A/B221/2427/8play Equal-tempered neutral seventh8, 24
1059.17 59 : 3259 : 25play Fifty-ninth harmonic[5]59
1066.76 B−50 : 272×52 : 33play Grave major seventh[3]5
1071.70 B♭-13 : 713 : 7play Tridecimal neutral seventh[21]13
1073.78 B119 : 647×17 : 26play Hundred-nineteenth harmonic[5]17
1075.00 243/48243/48play 43 steps in 48 equal temperament48
1086.31 C′♭−−4096 : 2187212 : 37play Pythagorean diminished octave[3][6]3
1088.27 B[2]15 : 83×5 : 23play Just major seventh,[3][5][11][16] small just major seventh,[4] ​1⁄6-comma meantone major seventh5
1095.04 C♭32 : 1725 : 17play 17th subharmonic[5][6]17
1100.00 B211/12211/12play Equal-tempered major seventh12M
1102.64 B↑↑♭-121 : 64112 : 26play Hundred-twenty-first harmonic[5]11
1107.82 C′♭−256 : 13528 : 33×5play Octave − major chroma,[3] 135th subharmonic, narrow diminished octave5
1109.78 B+[2]243 : 12835 : 27play Pythagorean major seventh[3][5][6][11]3
1116.88 61 : 3261 : 25play Sixty-first harmonic[5]61
1125.00 215/16245/48play 45 steps in 48 equal temperament16, 48
1129.33 C′♭[2]48 : 2524×3 : 52play Classic diminished octave,[3][6] large just major seventh[4]5
1131.02 B123 : 643×41 : 26play Hundred-twenty-third harmonic[5]41
1137.04 B27 : 1433 : 2×7play Septimal major seventh[5]7
1138.04 C♭247 : 12813×19 : 27play Two-hundred-forty-seventh harmonic19
1145.04 B31 : 1631 : 24play Thirty-first harmonic,[5] augmented seventh31
1146.73 C↓64 : 3326 : 3×11play 33rd subharmonic[6]11
1150.00 B/C223/24223/24play 23 steps in 24 equal temperament24
1151.23 C35 : 185×7 : 2×32play Septimal supermajor seventh, septimal quarter tone inverted 7
1158.94 B♯[2]125 : 6453 : 26play Just augmented seventh,[5] 125th harmonic5
1172.74 C+63 : 3232×7 : 25play Sixty-third harmonic[5]7
1175.00 247/48247/48play 47 steps in 48 equal temperament48
1178.49 C′−160 : 8125×5 : 34play Octave − syntonic comma,[3] semi-diminished octave5
1179.59 B↑253 : 12811×23 : 27play Two-hundred-fifty-third harmonic[5]23
1186.42 127 : 64127 : 26play Hundred-twenty-seventh harmonic[5]127
1200.00 C′2 : 12 : 1play Octave[3][11] or diapason[4]1, 123MS
1223.46 B♯+++531441 : 524288312 : 218play Pythagorean augmented seventh[3][6]3
1525.86 21/2+1play Silver ratio
1901.96 G′3 : 13 : 1play Tritave or just perfect twelfth3
2400.00 C″4 : 122 : 1play Fifteenth or two octaves1, 123M
3986.31 E‴10 : 15×2 : 1play Decade, compound just major third5M

See also

Notes
  1. Maneri-Sims notation

References
  1. Fox, Christopher (2003). "Microtones and Microtonalities", Contemporary Music Review, v. 22, pt. 1-2. (Abingdon, Oxfordshire, UK: Routledge): p.13.
  2. Fonville, John. 1991. "Ben Johnston's Extended Just Intonation: A Guide for Interpreters". Perspectives of New Music 29, no. 2 (Summer): 106–37.
  3. "List of intervals", Huygens-Fokker Foundation. The Foundation uses "classic" to indicate "just" or leaves off any adjective, as in "major sixth".
  4. Partch, Harry (1979). Genesis of a Music, p.68-69. ISBN 978-0-306-80106-8.
  5. "Anatomy of an Octave", KyleGann.com. Gann leaves off "just" but includes "5-limit". He uses "median" for "neutral".
  6. Haluška, Ján (2003). The Mathematical Theory of Tone Systems, p.xxv-xxix. ISBN 978-0-8247-4714-5.
  7. Ellis, Alexander J.; Hipkins, Alfred J. (1884), "Tonometrical Observations on Some Existing Non-Harmonic Musical Scales", Proceedings of the Royal Society of London, 37 (232–234): 368–385, doi:10.1098/rspl.1884.0041, JSTOR 114325, S2CID 122407786.
  8. "Logarithmic Interval Measures", Huygens-Fokker.org. Accessed 2015-06-06.
  9. "Orwell Temperaments", Xenharmony.org.
  10. Partch (1979), p.70.
  11. Alexander John Ellis (1885). On the musical scales of various nations, p.488. s.n.
  12. William Smythe Babcock Mathews (1895). Pronouncing dictionary and condensed encyclopedia of musical terms, p.13. ISBN 1-112-44188-3.
  13. Anger, Joseph Humfrey (1912). A treatise on harmony, with exercises, Volume 3, p.xiv-xv. W. Tyrrell.
  14. Hermann Ludwig F. von Helmholtz (Alexander John Ellis, trans.) (1875). "Additions by the translator", On the sensations of tone as a physiological basis for the theory of music, p.644. No ISBN specified.
  15. A. R. Meuss (2004). Intervals, Scales, Tones and the Concert Pitch C. Temple Lodge Publishing. p. 15. ISBN 1902636465.
  16. Paul, Oscar (1885). A manual of harmony for use in music-schools and seminaries and for self-instruction, p.165. Theodore Baker, trans. G. Schirmer. Paul uses "natural" for "just".
  17. "13th-harmonic", 31et.com.
  18. Brabner, John H. F. (1884). The National Encyclopaedia, Vol.13, p.182. London. [ISBN unspecified]
  19. Sabat, Marc and von Schweinitz, Wolfgang (2004). "The Extended Helmholtz-Ellis JI Pitch Notation" [PDF], NewMusicBox.org. Accessed: 04:12, 15 March 2014 (UTC).
  20. Hermann L. F Von Helmholtz (2007). On the Sensations of Tone, p.456. ISBN 978-1-60206-639-7.
  21. "Gallery of Just Intervals", Xenharmonic.wikispaces.com.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.