Paracompact uniform honeycombs
In geometry, uniform honeycombs in hyperbolic space are tessellations of convex uniform polyhedron cells. In 3-dimensional hyperbolic space there are 23 Coxeter group families of paracompact uniform honeycombs, generated as Wythoff constructions, and represented by ring permutations of the Coxeter diagrams for each family. These families can produce uniform honeycombs with infinite or unbounded facets or vertex figure, including ideal vertices at infinity, similar to the hyperbolic uniform tilings in 2-dimensions.
 {3,3,6}     |
 {6,3,3} |
 {4,3,6}  |
 {6,3,4} |
 {5,3,6}  |
 {6,3,5} |
 {6,3,6} |
 {3,6,3} |
 {4,4,3} |
 {3,4,4} |
 {4,4,4} |
Regular paracompact honeycombs
Of the uniform paracompact H3 honeycombs, 11 are regular, meaning that their group of symmetries acts transitively on their flags. These have Schläfli symbol {3,3,6}, {6,3,3}, {3,4,4}, {4,4,3}, {3,6,3}, {4,3,6}, {6,3,4}, {4,4,4}, {5,3,6}, {6,3,5}, and {6,3,6}, and are shown below. Four have finite Ideal polyhedral cells: {3,3,6}, {4,3,6}, {3,4,4}, and {5,3,6}.
| 11 paracompact regular honeycombs | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
{6,3,3} |
{6,3,4} |
{6,3,5} |
{6,3,6} |
{4,4,3} |
{4,4,4} | ||||||
{3,3,6} |
{4,3,6} |
{5,3,6} |
{3,6,3} |
{3,4,4} | |||||||
| Name | Schläfli Symbol {p,q,r} |
Coxeter   |
Cell type {p,q} |
Face type {p} |
Edge figure {r} |
Vertex figure {q,r} |
Dual | Coxeter group |
|---|---|---|---|---|---|---|---|---|
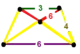
| Order-6 tetrahedral honeycomb | {3,3,6} | | {3,3} | {3} | {6} | {3,6} | {6,3,3} | [6,3,3] |
| Hexagonal tiling honeycomb | {6,3,3} | | {6,3} | {6} | {3} | {3,3} | {3,3,6} | |
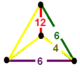
| Order-4 octahedral honeycomb | {3,4,4} | | {3,4} | {3} | {4} | {4,4} | {4,4,3} | [4,4,3] |
| Square tiling honeycomb | {4,4,3} | | {4,4} | {4} | {3} | {4,3} | {3,4,4} | |
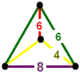
| Triangular tiling honeycomb | {3,6,3} | | {3,6} | {3} | {3} | {6,3} | Self-dual | [3,6,3] |
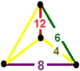
| Order-6 cubic honeycomb | {4,3,6} | | {4,3} | {4} | {4} | {3,4} | {6,3,4} | [6,3,4] |
| Order-4 hexagonal tiling honeycomb | {6,3,4} | | {6,3} | {6} | {4} | {3,4} | {4,3,6} | |
| Order-4 square tiling honeycomb | {4,4,4} | | {4,4} | {4} | {4} | {4,4} | Self-dual | [4,4,4] |
| Order-6 dodecahedral honeycomb | {5,3,6} | | {5,3} | {5} | {5} | {3,6} | {6,3,5} | [6,3,5] |
| Order-5 hexagonal tiling honeycomb | {6,3,5} | | {6,3} | {6} | {5} | {3,5} | {5,3,6} | |
| Order-6 hexagonal tiling honeycomb | {6,3,6} | | {6,3} | {6} | {6} | {3,6} | Self-dual | [6,3,6] |
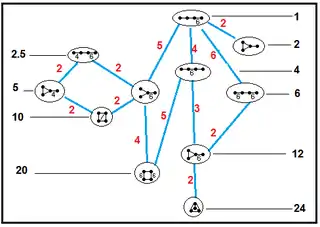
Coxeter groups of paracompact uniform honeycombs
 |
 |
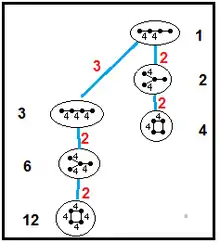| These graphs show subgroup relations of paracompact hyperbolic Coxeter groups. Order 2 subgroups represent bisecting a Goursat tetrahedron with a plane of mirror symmetry. | |
This is a complete enumeration of the 151 unique Wythoffian paracompact uniform honeycombs generated from tetrahedral fundamental domains (rank 4 paracompact coxeter groups). The honeycombs are indexed here for cross-referencing duplicate forms, with brackets around the nonprimary constructions.
The alternations are listed, but are either repeats or don't generate uniform solutions. Single-hole alternations represent a mirror removal operation. If an end-node is removed, another simplex (tetrahedral) family is generated. If a hole has two branches, a Vinberg polytope is generated, although only Vinberg polytope with mirror symmetry are related to the simplex groups, and their uniform honeycombs have not been systematically explored. These nonsimplectic (pyramidal) Coxeter groups are not enumerated on this page, except as special cases of half groups of the tetrahedral ones.
| Coxeter group | Simplex volume |
Commutator subgroup | Unique honeycomb count | |
|---|---|---|---|---|
| [6,3,3] | | 0.0422892336 | [1+,6,(3,3)+] = [3,3[3]]+ | 15 |
| [4,4,3] | | 0.0763304662 | [1+,4,1+,4,3+] | 15 |
| [3,3[3]] |   | 0.0845784672 | [3,3[3]]+ | 4 |
| [6,3,4] | | 0.1057230840 | [1+,6,3+,4,1+] = [3[]x[]]+ | 15 |
| [3,41,1] |   | 0.1526609324 | [3+,41+,1+] | 4 |
| [3,6,3] | | 0.1691569344 | [3+,6,3+] | 8 |
| [6,3,5] | | 0.1715016613 | [1+,6,(3,5)+] = [5,3[3]]+ | 15 |
| [6,31,1] | | 0.2114461680 | [1+,6,(31,1)+] = [3[]x[]]+ | 4 |
| [4,3[3]] | | 0.2114461680 | [1+,4,3[3]]+ = [3[]x[]]+ | 4 |
| [4,4,4] | | 0.2289913985 | [4+,4+,4+]+ | 6 |
| [6,3,6] | | 0.2537354016 | [1+,6,3+,6,1+] = [3[3,3]]+ | 8 |
| [(4,4,3,3)] |  | 0.3053218647 | [(4,1+,4,(3,3)+)] | 4 |
| [5,3[3]] | | 0.3430033226 | [5,3[3]]+ | 4 |
| [(6,3,3,3)] |    | 0.3641071004 | [(6,3,3,3)]+ | 9 |
| [3[]x[]] | | 0.4228923360 | [3[]x[]]+ | 1 |
| [41,1,1] | | 0.4579827971 | [1+,41+,1+,1+] | 0 |
| [6,3[3]] | | 0.5074708032 | [1+,6,3[3]] = [3[3,3]]+ | 2 |
| [(6,3,4,3)] |  | 0.5258402692 | [(6,3+,4,3+)] | 9 |
| [(4,4,4,3)] |  | 0.5562821156 | [(4,1+,4,1+,4,3+)] | 9 |
| [(6,3,5,3)] |  | 0.6729858045 | [(6,3,5,3)]+ | 9 |
| [(6,3,6,3)] | | 0.8457846720 | [(6,3+,6,3+)] | 5 |
| [(4,4,4,4)] | | 0.9159655942 | [(4+,4+,4+,4+)] | 1 |
| [3[3,3]] |  | 1.014916064 | [3[3,3]]+ | 0 |
The complete list of nonsimplectic (non-tetrahedral) paracompact Coxeter groups was published by P. Tumarkin in 2003.[1] The smallest paracompact form in H3 can be represented by 
or 
, or [∞,3,3,∞] which can be constructed by a mirror removal of paracompact hyperbolic group [3,4,4] as [3,4,1+,4] : 
= 
. The doubled fundamental domain changes from a tetrahedron into a quadrilateral pyramid. Another pyramid is or , constructed as [4,4,1+,4] = [∞,4,4,∞] : = .
Removing a mirror from some of the cyclic hyperbolic Coxeter graphs become bow-tie graphs: [(3,3,4,1+,4)] = [((3,∞,3)),((3,∞,3))] or 
, [(3,4,4,1+,4)] = [((4,∞,3)),((3,∞,4))] or 
, [(4,4,4,1+,4)] = [((4,∞,4)),((4,∞,4))] or 
. 
= 
, = , = .
Another nonsimplectic half groups is ↔ 
.
A radical nonsimplectic subgroup is 
↔ 
, which can be doubled into a triangular prism domain as 
↔ 
.
| Dimension | Rank | Graphs |
|---|---|---|
| H3 | 5 |
|
Linear graphs
[6,3,3] family
| # | Honeycomb name Coxeter diagram:     Schläfli symbol |
Cells by location (and count around each vertex) |
Vertex figure | Picture | ||||
|---|---|---|---|---|---|---|---|---|
| 1 |
2 |
3 |
4 |
Alt | ||||
| [137] | alternated hexagonal (  ↔  ) =  |
- | - | (4) (3.3.3.3.3.3) |
(4) (3.3.3) |
 (3.6.6) |
||
| [138] | cantic hexagonal ↔ |
(1) (3.3.3.3) |
- | (2) (3.6.3.6) |
(2) (3.6.6) |
 |
||
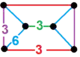| [139] | runcic hexagonal ↔ |
(1) (4.4.4) |
(1) (4.4.3) |
(1) (3.3.3.3.3.3) |
(3) (3.4.3.4) |
 |
||
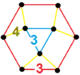| [140] | runcicantic hexagonal ↔ |
(1) (3.6.6) |
(1) (4.4.3) |
(1) (3.6.3.6) |
(2) (4.6.6) |
 |
||
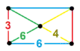| Nonuniform | snub rectified order-6 tetrahedral ↔ sr{3,3,6} |
 |
 |
 Irr. (3.3.3) |
 |
|||
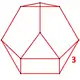| Nonuniform | cantic snub order-6 tetrahedral sr3{3,3,6} |
|||||||
| Nonuniform | omnisnub order-6 tetrahedral ht0,1,2,3{6,3,3} |
|
 |
Irr. (3.3.3) |
||||
[6,3,4] family
There are 15 forms, generated by ring permutations of the Coxeter group: [6,3,4] or
| # | Name of honeycomb Coxeter diagram Schläfli symbol |
Cells by location and count per vertex | Vertex figure | Picture | ||||
|---|---|---|---|---|---|---|---|---|
| 0 |
1 |
2 |
3 |
Alt | ||||
| [87] | alternated order-6 cubic ↔  h{4,3,6} |
(3.3.3) |
 (3.3.3.3.3.3) |
 (3.6.3.6) |
||||
| [88] | cantic order-6 cubic ↔ h2{4,3,6} |
(2) (3.6.6) |
- | - | (1) (3.6.3.6) |
(2) (6.6.6) |
 |
|
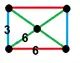| [89] | runcic order-6 cubic ↔ h3{4,3,6} |
(1) (3.3.3) |
- | - | (1) (6.6.6) |
(3) (3.4.6.4) |
 |
|
| [90] | runcicantic order-6 cubic ↔ h2,3{4,3,6} |
(1) (3.6.6) |
- | - | (1) (3.12.12) |
(2) (4.6.12) |
 |
|
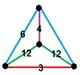| [141] | alternated order-4 hexagonal   ↔ ↔  h{6,3,4} |
- | - | (3.3.3.3.3.3) |
 (3.3.3.3) |
 (4.6.6) |
||
| [142] | cantic order-4 hexagonal ↔ ↔ h1{6,3,4} |
(1) (3.4.3.4) |
- | (2) (3.6.3.6) |
(2) (4.6.6) |
 |
||
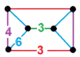| [143] | runcic order-4 hexagonal ↔ h3{6,3,4} |
(1) (4.4.4) |
(1) (4.4.3) |
(1) (3.3.3.3.3.3) |
(3) (3.4.4.4) |
 |
||
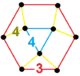| [144] | runcicantic order-4 hexagonal ↔ h2,3{6,3,4} |
(1) (3.8.8) |
(1) (4.4.3) |
(1) (3.6.3.6) |
(2) (4.6.8) |
 |
||
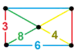| [151] | quarter order-4 hexagonal ↔ q{6,3,4} |
(3) |
(1) |
- | (1) |
(3) |
 |
|
| Nonuniform | bisnub order-6 cubic ↔ 2s{4,3,6} |
 (3.3.3.3.3.3) |
- | - | (3.3.3.3.6) |
+(3.3.3) |
 |
|
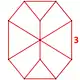| Nonuniform | runcic bisnub order-6 cubic |
|
|
|
|
|||
| Nonuniform | snub rectified order-6 cubic ↔ sr{4,3,6} |
 (3.3.3.3.3) |
 (3.3.3) |
 (3.3.3.4) |
(3.3.3.3.6) |
+(3.3.3) |
||
| Nonuniform | runcic snub rectified order-6 cubic sr3{4,3,6} |
|
|
|
|
|||
| Nonuniform | snub rectified order-4 hexagonal ↔  sr{6,3,4} |
(3.3.3.3.3.3) |
(3.3.3) |
- | (3.3.3.3.6) |
+(3.3.3) |
||
| Nonuniform | runcisnub rectified order-4 hexagonal sr3{6,3,4} |
|||||||
| Nonuniform | omnisnub rectified order-6 cubic ht0,1,2,3{6,3,4} |
(3.3.3.3.4) |
 (3.3.3.4) |
 (3.3.3.6) |
(3.3.3.3.6) |
+(3.3.3) |
||
[6,3,5] family
| # | Honeycomb name Coxeter diagram Schläfli symbol |
Cells by location (and count around each vertex) |
Vertex figure | Picture | ||||
|---|---|---|---|---|---|---|---|---|
0 |
1 |
2 |
3 |
Alt | ||||
| [145] | alternated order-5 hexagonal ↔ h{6,3,5} |
- | - | - | (20) (3)6 |
(12) (3)5 |
 (5.6.6) |
|
| [146] | cantic order-5 hexagonal ↔ h2{6,3,5} |
(1) (3.5.3.5) |
- | (2) (3.6.3.6) |
(2) (5.6.6) |
 |
||
| [147] | runcic order-5 hexagonal ↔ h3{6,3,5} |
(1) (5.5.5) |
(1) (4.4.3) |
(1) (3.3.3.3.3.3) |
(3) (3.4.5.4) |
 |
||
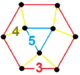| [148] | runcicantic order-5 hexagonal ↔ h2,3{6,3,5} |
(1) (3.10.10) |
(1) (4.4.3) |
(1) (3.6.3.6) |
(2) (4.6.10) |
 |
||
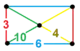| Nonuniform | snub rectified order-6 dodecahedral ↔ sr{5,3,6} |
 (3.3.5.3.5) |
- | (3.3.3.3) |
(3.3.3.3.3.3) |
irr. tet |
||
| Nonuniform | omnisnub order-5 hexagonal ht0,1,2,3{6,3,5} |
(3.3.5.3.5) |
 (3.3.3.5) |
(3.3.3.6) |
(3.3.6.3.6) |
irr. tet |
||
[6,3,6] family
There are 9 forms, generated by ring permutations of the Coxeter group: [6,3,6] or
| # | Name of honeycomb Coxeter diagram Schläfli symbol |
Cells by location and count per vertex | Vertex figure | Picture | |||
|---|---|---|---|---|---|---|---|
| 0 |
1 |
2 |
3 | ||||
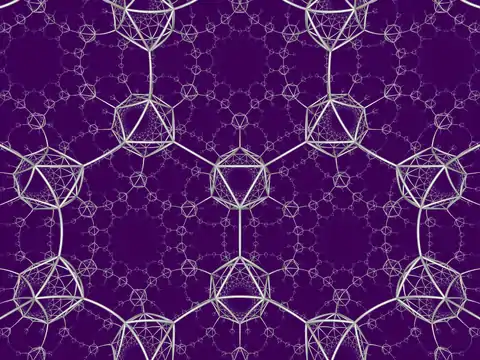
| 46 | order-6 hexagonal {6,3,6} |
- | - | - | (20) (6.6.6) |
(3.3.3.3.3.3) |
|
| 47 | rectified order-6 hexagonal t1{6,3,6} or r{6,3,6} |
(2) (3.3.3.3.3.3) |
- | - | (6) (3.6.3.6) |
 (6.4.4) |
 |
| 48 | truncated order-6 hexagonal t0,1{6,3,6} or t{6,3,6} |
(1) (3.3.3.3.3.3) |
- | - | (6) (3.12.12) |
 |
 |
| 49 | cantellated order-6 hexagonal t0,2{6,3,6} or rr{6,3,6} |
(1) (3.6.3.6) |
(2) (4.4.6) |
- | (2) (3.6.4.6) |
 |
 |
| 50 | Runcinated order-6 hexagonal t0,3{6,3,6} |
(1) (6.6.6) |
(3) (4.4.6) |
(3) (4.4.6) |
(1) (6.6.6) |
 |
 |
| 51 | cantitruncated order-6 hexagonal t0,1,2{6,3,6} or tr{6,3,6} |
(1) (6.6.6) |
(1) (4.4.6) |
- | (2) (4.6.12) |
 |
 |
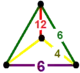| 52 | runcitruncated order-6 hexagonal t0,1,3{6,3,6} |
(1) (3.6.4.6) |
(1) (4.4.6) |
(2) (4.4.12) |
(1) (3.12.12) |
 |
 |
| 53 | omnitruncated order-6 hexagonal t0,1,2,3{6,3,6} |
(1) (4.6.12) |
(1) (4.4.12) |
(1) (4.4.12) |
(1) (4.6.12) |
 |
 |
| [1] | bitruncated order-6 hexagonal ↔  ↔  t1,2{6,3,6} or 2t{6,3,6} |
(2) (6.6.6) |
- | - | (2) (6.6.6) |
 |
 |
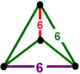| # | Name of honeycomb Coxeter diagram Schläfli symbol |
Cells by location and count per vertex | Vertex figure | Picture | ||||
|---|---|---|---|---|---|---|---|---|
| 0 |
1 |
2 |
3 |
Alt | ||||
| [47] | rectified order-6 hexagonal ↔    ↔ q{6,3,6} = r{6,3,6} |
(2) (3.3.3.3.3.3) |
- | - | (6) (3.6.3.6) |
(6.4.4) |
| |
| [54] | triangular ( ↔ ) = h{6,3,6} = {3,6,3} |
- | - | - | (3.3.3.3.3.3) |
(3.3.3.3.3.3) |
{6,3} |
|
| [55] | cantic order-6 hexagonal ( ↔ ) = h2{6,3,6} = r{3,6,3} |
(1) (3.6.3.6) |
- | (2) (6.6.6) |
(2) (3.6.3.6) |
 |
 | |
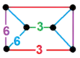| [149] | runcic order-6 hexagonal ↔ h3{6,3,6} |
(1) (6.6.6) |
(1) (4.4.3) |
(3) (3.4.6.4) |
(1) (3.3.3.3.3.3) |
 |
||
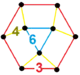| [150] | runcicantic order-6 hexagonal ↔ h2,3{6,3,6} |
(1) (3.12.12) |
(1) (4.4.3) |
(2) (4.6.12) |
(1) (3.6.3.6) |
 |
||
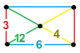| [137] | alternated hexagonal ( ↔ ↔ ) = 2s{6,3,6} = h{6,3,3} |
(3.3.3.3.6) |
- | - | (3.3.3.3.6) |
+(3.3.3) |
(3.6.6) |
|
| Nonuniform | snub rectified order-6 hexagonal sr{6,3,6} |
(3.3.3.3.3.3) |
(3.3.3.3) |
- | (3.3.3.3.6) |
+(3.3.3) |
||
| Nonuniform | alternated runcinated order-6 hexagonal ht0,3{6,3,6} |
(3.3.3.3.3.3) |
(3.3.3.3) |
(3.3.3.3) |
(3.3.3.3.3.3) |
+(3.3.3) |
||
| Nonuniform | omnisnub order-6 hexagonal ht0,1,2,3{6,3,6} |
(3.3.3.3.6) |
(3.3.3.6) |
(3.3.3.6) |
(3.3.3.3.6) |
+(3.3.3) |
||
[3,6,3] family
There are 9 forms, generated by ring permutations of the Coxeter group: [3,6,3] or
| # | Honeycomb name Coxeter diagram and Schläfli symbol |
Cell counts/vertex and positions in honeycomb |
Vertex figure | Picture | |||
|---|---|---|---|---|---|---|---|
| 0 |
1 |
2 |
3 | ||||
| 54 | triangular {3,6,3} |
- | - | - | (∞) {3,6} |
{6,3} |
|
| 55 | rectified triangular t1{3,6,3} or r{3,6,3} |
(2) (6)3 |
- | - | (3) (3.6)2 |
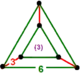 (3.4.4) |
|
| 56 | cantellated triangular t0,2{3,6,3} or rr{3,6,3} |
(1) (3.6)2 |
(2) (4.4.3) |
- | (2) (3.6.4.6) |
 |
 |
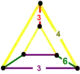| 57 | runcinated triangular t0,3{3,6,3} |
(1) (3)6 |
(6) (4.4.3) |
(6) (4.4.3) |
(1) (3)6 |
 |
 |
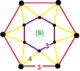| 58 | bitruncated triangular t1,2{3,6,3} or 2t{3,6,3} |
(2) (3.12.12) |
- | - | (2) (3.12.12) |
 |
 |
| 59 | cantitruncated triangular t0,1,2{3,6,3} or tr{3,6,3} |
(1) (3.12.12) |
(1) (4.4.3) |
- | (2) (4.6.12) |
 |
 |
| 60 | runcitruncated triangular t0,1,3{3,6,3} |
(1) (3.6.4.6) |
(1) (4.4.3) |
(2) (4.4.6) |
(1) (6)3 |
 |
 |
| 61 | omnitruncated triangular t0,1,2,3{3,6,3} |
(1) (4.6.12) |
(1) (4.4.6) |
(1) (4.4.6) |
(1) (4.6.12) |
 |
 |
| [1] | truncated triangular ↔ ↔ t0,1{3,6,3} or t{3,6,3} = {6,3,3} |
(1) (6)3 |
- | - | (3) (6)3 |
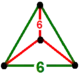 {3,3} |
 |
| # | Honeycomb name Coxeter diagram and Schläfli symbol |
Cell counts/vertex and positions in honeycomb |
Vertex figure | Picture | ||||
|---|---|---|---|---|---|---|---|---|
| 0 |
1 |
2 |
3 |
Alt | ||||
| [56] | cantellated triangular = s2{3,6,3} |
(1) (3.6)2 |
- | - | (2) (3.6.4.6) |
(3.4.4) |
|
|
| [60] | runcitruncated triangular = s2,3{3,6,3} |
(1) (6)3 |
- | (1) (4.4.3) |
(1) (3.6.4.6) |
(2) (4.4.6) |
|
|
| [137] | alternated hexagonal ( ↔ ) = ( ↔ )s{3,6,3} |
(3)6 |
- | - | (3)6 |
+(3)3 |
(3.6.6) |
|
| Scaliform | runcisnub triangular s3{3,6,3} |
r{6,3} |
- | (3.4.4) |
(3)6 |
 tricup |
||
| Nonuniform | omnisnub triangular tiling honeycomb ht0,1,2,3{3,6,3} |
(3.3.3.3.6) |
 (3)4 |
(3)4 |
(3.3.3.3.6) |
+(3)3 |
||
[4,4,3] family
There are 15 forms, generated by ring permutations of the Coxeter group: [4,4,3] or
| # | Honeycomb name Coxeter diagram and Schläfli symbol |
Cell counts/vertex and positions in honeycomb |
Vertex figure | Picture | |||
|---|---|---|---|---|---|---|---|
| 0 |
1 |
2 |
3 | ||||
| 62 | square = {4,4,3} |
- | - | - | (6) |
 Cube | |
| 63 | rectified square = t1{4,4,3} or r{4,4,3} |
(2) |
- | - | (3) |
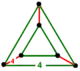 Triangular prism |  |
| 64 | rectified order-4 octahedral t1{3,4,4} or r{3,4,4} |
(4) |
- | - | (2) |
 |  |
| 65 | order-4 octahedral {3,4,4} |
(∞) |
- | - | - | |
|
| 66 | truncated square = t0,1{4,4,3} or t{4,4,3} |
(1) |
- | - | (3) |
 |  |
| 67 | truncated order-4 octahedral t0,1{3,4,4} or t{3,4,4} |
(4) |
- | - | (1) |  |  |
| 68 | bitruncated square t1,2{4,4,3} or 2t{4,4,3} |
(2) |
- | - | (2) |
 |  |
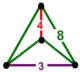| 69 | cantellated square t0,2{4,4,3} or rr{4,4,3} |
(1) |
(2) |
- | (2) |
 |  |
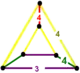| 70 | cantellated order-4 octahedral t0,2{3,4,4} or rr{3,4,4} |
(2) |
- | (2) |
(1) |
 |  |
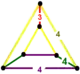| 71 | runcinated square t0,3{4,4,3} |
(1) |
(3) |
(3) |
(1) |
 |  |
| 72 | cantitruncated square t0,1,2{4,4,3} or tr{4,4,3} |
(1) |
(1) |
- | (2) |
 |  |
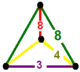| 73 | cantitruncated order-4 octahedral t0,1,2{3,4,4} or tr{3,4,4} |
(2) |
- | (1) |
(1) |
 |  |
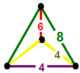| 74 | runcitruncated square t0,1,3{4,4,3} |
(1) |
(1) |
(2) |
(1) |
 |  |
| 75 | runcitruncated order-4 octahedral t0,1,3{3,4,4} |
(1) |
(2) |
(1) |
(1) |
 |  |
| 76 | omnitruncated square t0,1,2,3{4,4,3} |
(1) |
(1) |
(1) |
(1) |
 |  |
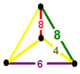| # | Honeycomb name Coxeter diagram and Schläfli symbol |
Cell counts/vertex and positions in honeycomb |
Vertex figure | Picture | ||||
|---|---|---|---|---|---|---|---|---|
| 0 |
1 |
2 |
3 |
Alt | ||||
| [83] | alternated square ↔ h{4,4,3} | - | - | - | | {4,3} | (4.3.4.3) | |
| [84] | cantic square ↔ h2{4,4,3} |
(3.4.3.4) |
- | (3.8.8) |
(4.8.8) |
 |
||
| [85] | runcic square ↔ h3{4,4,3} |
(3.3.3.3) |
- | (3.4.4.4) |
(4.4.4) |
 |
||
| [86] | runcicantic square ↔ |
(4.6.6) |
- | (3.4.4.4) |
(4.8.8) |
 |
||
| Nonsimplectic | alternated rectified square ↔  hr{4,4,3} | | - | - | | {}x{3} | ||
| Scaliform | snub order-4 octahedral = = s{3,4,4} | | - | - | | {}v{4} | ||
| Scaliform | runcisnub order-4 octahedral s3{3,4,4} | | | | | cup-4 | ||
| 152 | snub square = s{4,4,3} | | - | - |  | {3,3} |  | |
| Nonuniform | snub rectified order-4 octahedral sr{3,4,4} | | - | | | irr. {3,3} | ||
| Nonuniform | alternated runcitruncated square ht0,1,3{3,4,4} | | | | | irr. {}v{4} | ||
| Nonuniform | omnisnub square ht0,1,2,3{4,4,3} |  | | |  | irr. {3,3} | ||
[4,4,4] family
There are 9 forms, generated by ring permutations of the Coxeter group: [4,4,4] or .
| # | Honeycomb name Coxeter diagram and Schläfli symbol |
Cell counts/vertex and positions in honeycomb |
Symmetry | Vertex figure | Picture | |||
|---|---|---|---|---|---|---|---|---|
| 0 |
1 |
2 |
3 | |||||
| 77 | order-4 square {4,4,4} | - | - | - | | [4,4,4] |  Cube | |
| 78 | truncated order-4 square t0,1{4,4,4} or t{4,4,4} | | - | - | | [4,4,4] |  |  |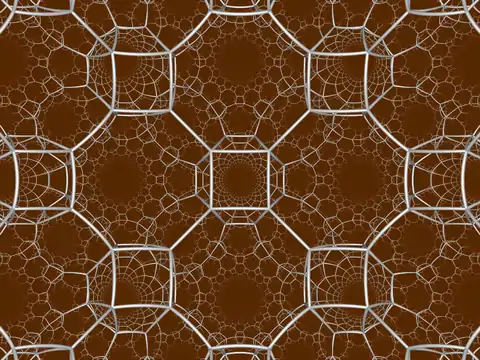
| 79 | bitruncated order-4 square t1,2{4,4,4} or 2t{4,4,4} | | - | - | | [[4,4,4]] |  |  |
| 80 | runcinated order-4 square t0,3{4,4,4} | | | | | [[4,4,4]] |  |  |
| 81 | runcitruncated order-4 square t0,1,3{4,4,4} | | | | | [4,4,4] |  |  |
| 82 | omnitruncated order-4 square t0,1,2,3{4,4,4} | | | | | [[4,4,4]] |  |  |
| [62] | square ↔ t1{4,4,4} or r{4,4,4} | | - | - | | [4,4,4] | Square tiling | |
| [63] | rectified square ↔ t0,2{4,4,4} or rr{4,4,4} | | | - | | [4,4,4] |  |  |
| [66] | truncated order-4 square ↔ t0,1,2{4,4,4} or tr{4,4,4} | | | - | | [4,4,4] |  |  |
| # | Honeycomb name Coxeter diagram and Schläfli symbol |
Cell counts/vertex and positions in honeycomb |
Symmetry | Vertex figure | Picture | ||||
|---|---|---|---|---|---|---|---|---|---|
| 0 |
1 |
2 |
3 |
Alt | |||||
| [62] | Square ( ↔ ↔  ↔ ) = |
(4.4.4.4) |
- | - | (4.4.4.4) |
[1+,4,4,4] =[4,4,4] |
|
| |
| [63] | rectified square = s2{4,4,4} | | | - | | [4+,4,4] | | | |
| [77] | order-4 square ↔ ↔ ↔ | - | - | - | |
| [1+,4,4,4] =[4,4,4] | Cube | |
| [78] | truncated order-4 square ↔ ↔ ↔ |
(4.8.8) |
- | (4.8.8) |
- | (4.4.4.4) |
[1+,4,4,4] =[4,4,4] |
|
|
| [79] | bitruncated order-4 square ↔ ↔ ↔ |
(4.8.8) |
- | - | (4.8.8) |
(4.8.8) |
[1+,4,4,4] =[4,4,4] |
|
|
| [81] | runcitruncated order-4 square tiling = s2,3{4,4,4} | | | | | [4,4,4] | | | |
| [83] | alternated square ( ↔ ) ↔ hr{4,4,4} | | - | - | | | [4,1+,4,4] | (4.3.4.3) | |
| [104] | quarter order-4 square ↔ q{4,4,4} |
[[1+,4,4,4,1+]] =[[4[4]]] |  | ||||||
| 153 | alternated rectified square tiling ↔ ↔ hrr{4,4,4} | | | - | | [((2+,4,4)),4] | |||
| 154 | alternated runcinated order-4 square tiling ht0,3{4,4,4} | | | | | [[(4,4,4,2+)]] |  | ||
| Scaliform | snub order-4 square tiling s{4,4,4} | | - | - | | [4+,4,4] | |||
| Nonuniform | runcic snub order-4 square tiling s3{4,4,4} | [4+,4,4] | |||||||
| Nonuniform | bisnub order-4 square tiling 2s{4,4,4} | | - | - | | [[4,4+,4]] |  | ||
| [152] | snub square tiling ↔ sr{4,4,4} | | | - | | [(4,4)+,4] | | ||
| Nonuniform | alternated runcitruncated order-4 square tiling ht0,1,3{4,4,4} | | | | | [((2,4)+,4,4)] | |||
| Nonuniform | omnisnub order-4 square tiling ht0,1,2,3{4,4,4} | | | | | [[4,4,4]]+ | |||
Tridental graphs
[3,41,1] family
There are 11 forms (of which only 4 are not shared with the [4,4,3] family), generated by ring permutations of the Coxeter group:
| # | Honeycomb name Coxeter diagram |
Cells by location (and count around each vertex) |
Vertex figure | Picture | |||
|---|---|---|---|---|---|---|---|
0   |
1 |
0' |
3 | ||||
| 83 | alternated square ↔ |
- | - | (4.4.4) |
(4.4.4.4) |
(4.3.4.3) |
|
| 84 | cantic square ↔ |
(3.4.3.4) |
- | (3.8.8) |
(4.8.8) |
|
|
| 85 | runcic square ↔ |
(4.4.4.4) |
- | (3.4.4.4) |
(4.4.4.4) |
|
|
| 86 | runcicantic square ↔ |
(4.6.6) |
- | (3.4.4.4) |
(4.8.8) |
|
|
| [63] | rectified square ↔ |
(4.4.4) |
- | (4.4.4) |
(4.4.4.4) |
|
|
| [64] | rectified order-4 octahedral ↔ |
(3.4.3.4) |
- | (3.4.3.4) |
(4.4.4.4) |
|
|
| [65] | order-4 octahedral ↔ |
(4.4.4.4) |
- | (4.4.4.4) |
- | |
|
| [67] | truncated order-4 octahedral ↔ |
(4.6.6) |
- | (4.6.6) |
(4.4.4.4) |
|
|
| [68] | bitruncated square ↔ |
(3.8.8) |
- | (3.8.8) |
(4.8.8) |
|
|
| [70] | cantellated order-4 octahedral ↔ |
(3.4.4.4) |
 (4.4.4) |
(3.4.4.4) |
(4.4.4.4) |
|
|
| [73] | cantitruncated order-4 octahedral ↔ |
(4.6.8) |
(4.4.4) |
(4.6.8) |
(4.8.8) |
|
|
| # | Honeycomb name Coxeter diagram |
Cells by location (and count around each vertex) |
Vertex figure | Picture | ||||
|---|---|---|---|---|---|---|---|---|
| 0 |
1 |
0' |
3 |
Alt | ||||
| Scaliform | snub order-4 octahedral = = s{3,41,1} | | - | - | | irr. {}v{4} | ||
| Nonuniform | snub rectified order-4 octahedral ↔ sr{3,41,1} |
(3.3.3.3.4) |
(3.3.3) |
(3.3.3.3.4) |
(3.3.4.3.4) |
+(3.3.3) |
||
[4,41,1] family
There are 7 forms, (all shared with [4,4,4] family), generated by ring permutations of the Coxeter group:
| # | Honeycomb name Coxeter diagram |
Cells by location | Vertex figure | Picture | |||
|---|---|---|---|---|---|---|---|
| 0 |
1 |
0' |
3 | ||||
| [62] | Square ( ↔ ) = |
(4.4.4.4) |
- | (4.4.4.4) |
(4.4.4.4) |
|
|
| [62] | Square ( ↔ ) = |
(4.4.4.4) |
- | (4.4.4.4) |
(4.4.4.4) |
|
|
| [63] | rectified square ( ↔ ) = |
(4.4.4.4) |
(4.4.4) |
(4.4.4.4) |
(4.4.4.4) |
|
|
| [66] | truncated square ( ↔ ) = |
(4.8.8) |
(4.4.4) |
(4.8.8) |
(4.8.8) |
|
|
| [77] | order-4 square ↔ |
(4.4.4.4) |
- | (4.4.4.4) |
- | |
|
| [78] | truncated order-4 square ↔ |
(4.8.8) |
- | (4.8.8) |
(4.4.4.4) |
|
|
| [79] | bitruncated order-4 square ↔ |
(4.8.8) |
- | (4.8.8) |
(4.8.8) |
|
|
| # | Honeycomb name Coxeter diagram |
Cells by location (and count around each vertex) |
Vertex figure | Picture | ||||
|---|---|---|---|---|---|---|---|---|
| 0 |
1 |
0' |
3 |
Alt | ||||
| [77] | order-4 square ( ↔ ↔ ) = |
|
- | |
- | Cube |
|
|
| [78] | truncated order-4 square ( ↔ ) = ( ↔ ) |
|
|
|
|
|
| |
| [83] | Alternated square ↔ |
|
- | |
|
|
 |
|
| Scaliform | Snub order-4 square |
|
- | |
|
|||
| Nonuniform | |
|
- | |
|
|||
| Nonuniform | |
|
- | |
|
|||
| Nonsimplectic | ( ↔ ) = ( ↔ ) |
|
|
|
|
|||
| Nonuniform | Snub square ↔ ↔ |
(3.3.4.3.4) |
(3.3.3) |
(3.3.4.3.4) |
(3.3.4.3.4) |
+(3.3.3) |
||
[6,31,1] family
There are 11 forms (and only 4 not shared with [6,3,4] family), generated by ring permutations of the Coxeter group: [6,31,1] or .
| # | Honeycomb name Coxeter diagram |
Cells by location (and count around each vertex) |
Vertex figure | Picture | |||
|---|---|---|---|---|---|---|---|
0 |
1 |
0' |
3 | ||||
| 87 | alternated order-6 cubic ↔ |
- | - | (∞) (3.3.3.3.3) |
(∞) (3.3.3) |
(3.6.3.6) |
|
| 88 | cantic order-6 cubic ↔ |
(1) (3.6.3.6) |
- | (2) (6.6.6) |
(2) (3.6.6) |
|
|
| 89 | runcic order-6 cubic ↔ |
(1) (6.6.6) |
- | (3) (3.4.6.4) |
(1) (3.3.3) |
|
|
| 90 | runcicantic order-6 cubic ↔ |
(1) (3.12.12) |
- | (2) (4.6.12) |
(1) (3.6.6) |
|
|
| [16] | order-4 hexagonal ↔ |
(4) (6.6.6) |
- | (4) (6.6.6) |
- |  (3.3.3.3) |
|
| [17] | rectified order-4 hexagonal ↔ |
(2) (3.6.3.6) |
- | (2) (3.6.3.6) |
(2) (3.3.3.3) |
 |
 |
| [18] | rectified order-6 cubic ↔ |
(1) (3.3.3.3.3) |
- | (1) (3.3.3.3.3) |
(6) (3.4.3.4) |
 |
 |
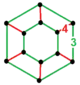| [20] | truncated order-4 hexagonal ↔ |
(2) (3.12.12) |
- | (2) (3.12.12) |
(1) (3.3.3.3) |
 |
 |
| [21] | bitruncated order-6 cubic ↔ |
(1) (6.6.6) |
- | (1) (6.6.6) |
(2) (4.6.6) |
 |
 |
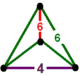| [24] | cantellated order-6 cubic ↔ |
(1) (3.4.6.4) |
(2) (4.4.4) |
(1) (3.4.6.4) |
(1) (3.4.3.4) |
|
 |
| [27] | cantitruncated order-6 cubic ↔ |
(1) (4.6.12) |
(1) (4.4.4) |
(1) (4.6.12) |
(1) (4.6.6) |
 |
 |
| # | Honeycomb name Coxeter diagram |
Cells by location (and count around each vertex) |
Vertex figure | Picture | ||||
|---|---|---|---|---|---|---|---|---|
| 0 |
1 |
0' |
3 |
Alt | ||||
| [141] | alternated order-4 hexagonal ↔ ↔  ↔ |
(4.6.6) |
||||||
| Nonuniform | bisnub order-4 hexagonal ↔ |
|
||||||
| Nonuniform | snub rectified order-4 hexagonal ↔ |
(3.3.3.3.6) |
(3.3.3) |
(3.3.3.3.6) |
(3.3.3.3.3) |
+(3.3.3) |
||
Cyclic graphs
[(4,4,3,3)] family
There are 11 forms, 4 unique to this family, generated by ring permutations of the Coxeter group: , with ↔ .
| # | Honeycomb name Coxeter diagram |
Cells by location | Vertex figure | Picture | |||
|---|---|---|---|---|---|---|---|
| 0 |
1 |
2 |
3 | ||||
| 91 | tetrahedral-square |
- | (6) (444) |
(8) (333) |
(12) (3434) |
(3444) |
|
| 92 | cyclotruncated square-tetrahedral |
(444) |
(488) |
(333) |
(388) |
 |
|
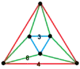| 93 | cyclotruncated tetrahedral-square |
(1) (3333) |
(1) (444) |
(4) (366) |
(4) (466) |
 |
|
| 94 | truncated tetrahedral-square |
(1) (3444) |
(1) (488) |
(1) (366) |
(2) (468) |
 |
|
| [64] | ( ↔ ) = rectified order-4 octahedral |
(3434) |
(4444) |
(3434) |
(3434) |
|
|
| [65] | ( ↔  ) = order-4 octahedral |
(3333) |
- | (3333) |
(3333) |
|
|
| [67] | ( ↔ ) = truncated order-4 octahedral |
(466) |
(4444) |
(3434) |
(466) |
|
|
| [83] | alternated square ( ↔ ) = |
(444) |
(4444) |
- | (444) |
(4.3.4.3) |
|
| [84] | cantic square ( ↔ ) = |
(388) |
(488) |
(3434) |
(388) |
|
|
| [85] | runcic square ( ↔ ) = |
(3444) |
(3434) |
(3333) |
(3444) |
|
|
| [86] | runcicantic square ( ↔ ) = |
(468) |
(488) |
(466) |
(468) |
|
|
| # | Honeycomb name Coxeter diagram |
Cells by location | Vertex figure | Picture | ||||
|---|---|---|---|---|---|---|---|---|
| 0 |
1 |
2 |
3 |
Alt | ||||
| Scaliform | snub order-4 octahedral = = | | - | - | | irr. {}v{4} | ||
| Nonuniform | | | | | | |||
| Nonsimplectic | alternated tetrahedral-square ↔   | | | | ||||
[(4,4,4,3)] family
There are 9 forms, generated by ring permutations of the Coxeter group: .
| # | Honeycomb name Coxeter diagram |
Cells by location (and count around each vertex) |
Vertex figure | Picture | |||
|---|---|---|---|---|---|---|---|
| 0 |
1 |
2 |
3 | ||||
| 95 | cubic-square |
(8) (4.4.4) |
- | (6) (4.4.4.4) |
(12) (4.4.4.4) |
(3.4.4.4) |
|
| 96 | octahedral-square |
(3.4.3.4) |
(3.3.3.3) |
- | (4.4.4.4) |
(4.4.4.4) |
|
| 97 | cyclotruncated cubic-square |
(4) (3.8.8) |
(1) (3.3.3.3) |
(1) (4.4.4.4) |
(4) (4.8.8) |
 |
|
| 98 | cyclotruncated square-cubic |
(1) (4.4.4) |
(1) (4.4.4) |
(3) (4.8.8) |
(3) (4.8.8) |
 |
|
| 99 | cyclotruncated octahedral-square |
(4) (4.6.6) |
(4) (4.6.6) |
(1) (4.4.4.4) |
(1) (4.4.4.4) |
 |
|
| 100 | rectified cubic-square |
(1) (3.4.3.4) |
(2) (3.4.4.4) |
(1) (4.4.4.4) |
(2) (4.4.4.4) |
 |
|
| 101 | truncated cubic-square |
(1) (4.8.8) |
(1) (3.4.4.4) |
(2) (4.8.8) |
(1) (4.8.8) |
 |
|
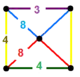| 102 | truncated octahedral-square |
(2) (4.6.8 |
(1) (4.6.6) |
(1) (4.4.4.4) |
(1) (4.8.8) |
 |
|
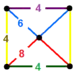| 103 | omnitruncated octahedral-square |
(1) (4.6.8) |
(1) (4.6.8) |
(1) (4.8.8) |
(1) (4.8.8) |
 |
|
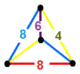| # | Honeycomb name Coxeter diagram |
Cells by location (and count around each vertex) |
Vertex figure | ||||
|---|---|---|---|---|---|---|---|
| 0 |
1 |
2 |
3 |
Alt | |||
| Nonsimplectic | alternated cubic-square ↔ |
- | |
|
|
(3.4.4.4) |
|
| Nonuniform | snub octahedral-square |
|
 |
|
|
||
| Nonuniform | cyclosnub square-cubic |
|
|
|
|
||
| Nonuniform | cyclosnub octahedral-square |
|
|
|
|
||
| Nonuniform | omnisnub cubic-square |
(3.3.3.3.4) |
(3.3.3.3.4) |
(3.3.4.3.4) |
(3.3.4.3.4) |
+(3.3.3) |
|
[(4,4,4,4)] family
There are 5 forms, 1 unique, generated by ring permutations of the Coxeter group: . Repeat constructions are related as: ↔ , ↔ , and 
↔ .
| # | Honeycomb name Coxeter diagram |
Cells by location (and count around each vertex) |
Vertex figure | Picture | |||
|---|---|---|---|---|---|---|---|
| 0 |
1 |
2 |
3 | ||||
| 104 | quarter order-4 square ↔ |
(4.8.8) |
(4.4.4.4) |
(4.4.4.4) |
(4.8.8) |
|
|
| [62] | square ↔ ↔ |
(4.4.4.4) |
(4.4.4.4) |
(4.4.4.4) |
(4.4.4.4) |
|
|
| [77] | order-4 square ( ↔ ) = |
(4.4.4.4) |
- | (4.4.4.4) |
(4.4.4.4) |
(4.4.4.4) |
|
| [78] | truncated order-4 square ( ↔ ) = |
(4.8.8) |
(4.4.4.4) |
(4.8.8) |
(4.8.8) |
|
|
| [79] | bitruncated order-4 square ↔ |
(4.8.8) |
(4.8.8) |
(4.8.8) |
(4.8.8) |
|
|
| # | Honeycomb name Coxeter diagram |
Cells by location (and count around each vertex) |
Vertex figure | ||||
|---|---|---|---|---|---|---|---|
| 0 |
1 |
2 |
3 |
Alt | |||
| [83] | alternated square ( ↔ ↔ ) = |
(6) (4.4.4.4) |
(6) (4.4.4.4) |
(6) (4.4.4.4) |
(6) (4.4.4.4) |
(8) (4.4.4) |
(4.3.4.3) |
| Nonsimplectic | alternated order-4 square ↔ |
|
- | |
|
||
| Nonsimplectic | cantic order-4 square ↔ |
|
|
|
|
||
| Nonuniform | cyclosnub square |
|
|
|
|
||
| Nonuniform | snub order-4 square |
|
|
|
|
||
| Nonuniform | bisnub order-4 square ↔ |
(3.3.4.3.4) |
(3.3.4.3.4) |
(3.3.4.3.4) |
(3.3.4.3.4) |
+(3.3.3) |
|
[(6,3,3,3)] family
There are 9 forms, generated by ring permutations of the Coxeter group: .
| # | Honeycomb name Coxeter diagram |
Cells by location (and count around each vertex) |
Vertex figure | |||
|---|---|---|---|---|---|---|
| 0 |
1  |
2 |
3 | |||
| 105 | tetrahedral-hexagonal |
(4) (3.3.3) |
- | (4) (6.6.6) |
(6) (3.6.3.6) |
 (3.4.3.4) |
| 106 | tetrahedral-triangular |
(3.3.3.3) |
(3.3.3) |
- | (3.3.3.3.3.3) |
(3.4.6.4) |
| 107 | cyclotruncated tetrahedral-hexagonal |
(3) (3.6.6) |
(1) (3.3.3) |
(1) (6.6.6) |
(3) (6.6.6) |
 |
| 108 | cyclotruncated hexagonal-tetrahedral |
(1) (3.3.3) |
(1) (3.3.3) |
(4) (3.12.12) |
(4) (3.12.12) |
 |
| 109 | cyclotruncated tetrahedral-triangular |
(6) (3.6.6) |
(6) (3.6.6) |
(1) (3.3.3.3.3.3) |
(1) (3.3.3.3.3.3) |
 |
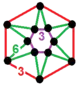| 110 | rectified tetrahedral-hexagonal |
(1) (3.3.3.3) |
(2) (3.4.3.4) |
(1) (3.6.3.6) |
(2) (3.4.6.4) |
 |
| 111 | truncated tetrahedral-hexagonal |
(1) (3.6.6) |
(1) (3.4.3.4) |
(1) (3.12.12) |
(2) (4.6.12) |
 |
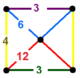| 112 | truncated tetrahedral-triangular |
(2) (4.6.6) |
(1) (3.6.6) |
(1) (3.4.6.4) |
(1) (6.6.6) |
 |
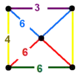| 113 | omnitruncated tetrahedral-hexagonal |
(1) (4.6.6) |
(1) (4.6.6) |
(1) (4.6.12) |
(1) (4.6.12) |
 |
| # | Honeycomb name Coxeter diagram |
Cells by location (and count around each vertex) |
Vertex figure | ||||
|---|---|---|---|---|---|---|---|
| 0 |
1 |
2 |
3 |
Alt | |||
| Nonuniform | omnisnub tetrahedral-hexagonal |
(3.3.3.3.3) |
(3.3.3.3.3) |
(3.3.3.3.6) |
(3.3.3.3.6) |
+(3.3.3) |
 |
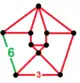[(6,3,4,3)] family
There are 9 forms, generated by ring permutations of the Coxeter group:
| # | Honeycomb name Coxeter diagram |
Cells by location (and count around each vertex) |
Vertex figure | |||
|---|---|---|---|---|---|---|
| 0 |
1 |
2 |
3 | |||
| 114 | octahedral-hexagonal |
(6) (3.3.3.3)  |
- | (8) (6.6.6)  |
(12) (3.6.3.6)  |
 |
| 115 | cubic-triangular |
(∞) (3.4.3.4) |
(∞) (4.4.4) |
- | (∞) (3.3.3.3.3.3) |
(3.4.6.4) |
| 116 | cyclotruncated octahedral-hexagonal |
(3) (4.6.6) |
(1) (4.4.4) |
(1) (6.6.6) |
(3) (6.6.6) |
 |
| 117 | cyclotruncated hexagonal-octahedral |
(1) (3.3.3.3) |
(1) (3.3.3.3) |
(4) (3.12.12) |
(4) (3.12.12) |
 |
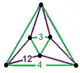| 118 | cyclotruncated cubic-triangular |
(6) (3.8.8) |
(6) (3.8.8) |
(1) (3.3.3.3.3.3) |
(1) (3.3.3.3.3.3) |
 |
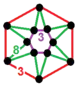| 119 | rectified octahedral-hexagonal |
(1) (3.4.3.4) |
(2) (3.4.4.4) |
(1) (3.6.3.6) |
(2) (3.4.6.4) |
 |
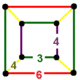| 120 | truncated octahedral-hexagonal |
(1) (4.6.6) |
(1) (3.4.4.4) |
(1) (3.12.12) |
(2) (4.6.12) |
 |
| 121 | truncated cubic-triangular |
(2) (4.6.8) |
(1) (3.8.8) |
(1) (3.4.6.4) |
(1) (6.6.6) |
 |
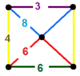| 122 | omnitruncated octahedral-hexagonal |
(1) (4.6.8) |
(1) (4.6.8) |
(1) (4.6.12) |
(1) (4.6.12) |
 |
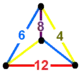| # | Honeycomb name Coxeter diagram |
Cells by location (and count around each vertex) |
Vertex figure | ||||
|---|---|---|---|---|---|---|---|
| 0 |
1 |
2 |
3 |
Alt | |||
| Nonuniform | cyclosnub octahedral-hexagonal  |
(3.3.3.3.3)   |
(3.3.3) |
(3.3.3.3.3.3) |
(3.3.3.3.3.3) |
irr. {3,4} |
 |
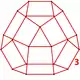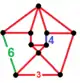
| Nonuniform | omnisnub octahedral-hexagonal |
(3.3.3.3.4) |
(3.3.3.3.4)  |
(3.3.3.3.6) |
(3.3.3.3.6) |
irr. {3,3} |
 |
[(6,3,5,3)] family
There are 9 forms, generated by ring permutations of the Coxeter group:
| # | Honeycomb name Coxeter diagram |
Cells by location (and count around each vertex) |
Vertex figure | Picture | |||
|---|---|---|---|---|---|---|---|
| 0 |
1 |
2 |
3 | ||||
| 123 | icosahedral-hexagonal |
(6) (3.3.3.3.3) |
- | (8) (6.6.6) |
(12) (3.6.3.6) |
3.4.5.4 |
|
| 124 | dodecahedral-triangular |
(30) (3.5.3.5) |
(20) (5.5.5) |
- | (12) (3.3.3.3.3.3) |
(3.4.6.4) |
|
| 125 | cyclotruncated icosahedral-hexagonal |
(3) (5.6.6) |
(1) (5.5.5) |
(1) (6.6.6) |
(3) (6.6.6) |
 |
|
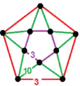
| 126 | cyclotruncated hexagonal-icosahedral |
(1) (3.3.3.3.3) |
(1) (3.3.3.3.3) |
(5) (3.12.12) |
(5) (3.12.12) |
 |
|
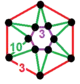
| 127 | cyclotruncated dodecahedral-triangular |
(6) (3.10.10) |
(6) (3.10.10) |
(1) (3.3.3.3.3.3) |
(1) (3.3.3.3.3.3) |
 |
|
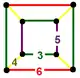
| 128 | rectified icosahedral-hexagonal |
(1) (3.5.3.5) |
(2) (3.4.5.4) |
(1) (3.6.3.6) |
(2) (3.4.6.4) |
 |
|
| 129 | truncated icosahedral-hexagonal |
(1) (5.6.6) |
(1) (3.5.5.5) |
(1) (3.12.12) |
(2) (4.6.12) |
 |
|
| 130 | truncated dodecahedral-triangular |
(2) (4.6.10) |
(1) (3.10.10) |
(1) (3.4.6.4) |
(1) (6.6.6) |
 |
|
| 131 | omnitruncated icosahedral-hexagonal |
(1) (4.6.10) |
(1) (4.6.10) |
(1) (4.6.12) |
(1) (4.6.12) |
 |
|
| # | Honeycomb name Coxeter diagram |
Cells by location (and count around each vertex) |
Vertex figure | Picture | ||||
|---|---|---|---|---|---|---|---|---|
| 0 |
1 |
2 |
3 |
Alt | ||||
| Nonuniform | omnisnub icosahedral-hexagonal |
 (3.3.3.3.5) |
(3.3.3.3.5) |
(3.3.3.3.6) |
(3.3.3.3.6) |
+(3.3.3) |
 |
|
[(6,3,6,3)] family
There are 6 forms, generated by ring permutations of the Coxeter group: .
| # | Honeycomb name Coxeter diagram |
Cells by location (and count around each vertex) |
Vertex figure | Picture | |||
|---|---|---|---|---|---|---|---|
| 0 |
1 |
2 |
3 | ||||
| 132 | hexagonal-triangular |
(3.3.3.3.3.3) |
- | (6.6.6) |
(3.6.3.6) |
(3.4.6.4) |
|
| 133 | cyclotruncated hexagonal-triangular |
(1) (3.3.3.3.3.3) |
(1) (3.3.3.3.3.3) |
(3) (3.12.12) |
(3) (3.12.12) |
 |
|
| 134 | cyclotruncated triangular-hexagonal |
(1) (3.6.3.6) |
(2) (3.4.6.4) |
(1) (3.6.3.6) |
(2) (3.4.6.4) |
 |
|
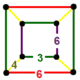| 135 | rectified hexagonal-triangular |
(1) (6.6.6) |
(1) (3.4.6.4) |
(1) (3.12.12) |
(2) (4.6.12) |
 |
|
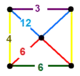| 136 | truncated hexagonal-triangular |
(1) (4.6.12) |
(1) (4.6.12) |
(1) (4.6.12) |
(1) (4.6.12) |
 |
|
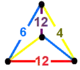| [16] | order-4 hexagonal tiling = |
(3) (6.6.6) |
(1) (6.6.6) |
(1) (6.6.6) |
(3) (6.6.6) |
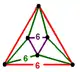 (3.3.3.3) |
|
| # | Honeycomb name Coxeter diagram |
Cells by location (and count around each vertex) |
Vertex figure | Picture | ||||
|---|---|---|---|---|---|---|---|---|
| 0 |
1 |
2 |
3 |
Alt | ||||
| [141] | alternated order-4 hexagonal ↔ ↔ ↔ |
(3.3.3.3.3.3) |
(3.3.3.3.3.3) |
(3.3.3.3.3.3) |
(3.3.3.3.3.3) |
+(3.3.3.3) |
(4.6.6) |
|
| Nonuniform | cyclocantisnub hexagonal-triangular |
|||||||
| Nonuniform | cycloruncicantisnub hexagonal-triangular |
|||||||
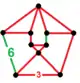
| Nonuniform | snub rectified hexagonal-triangular |
(3.3.3.3.6) |
(3.3.3.3.6) |
(3.3.3.3.6) |
(3.3.3.3.6) |
+(3.3.3) |
 |
|
Loop-n-tail graphs
[3,3[3]] family
There are 11 forms, 4 unique, generated by ring permutations of the Coxeter group: [3,3[3]] or . 7 are half symmetry forms of [3,3,6]: 
↔ .
| # | Honeycomb name Coxeter diagram |
Cells by location (and count around each vertex) |
vertex figure | Picture | |||
|---|---|---|---|---|---|---|---|
| 0 |
1 |
0' |
3 | ||||
| 137 | alternated hexagonal ( ↔ ) = |
- | - | (3.3.3) |
(3.3.3.3.3.3) |
(3.6.6) |
|
| 138 | cantic hexagonal ↔ |
(1) (3.3.3.3) |
- | (2) (3.6.6) |
(2) (3.6.3.6) |
|
|
| 139 | runcic hexagonal ↔ |
(1) (4.4.4) |
(1) (4.4.3) |
(3) (3.4.3.4) |
(1) (3.3.3.3.3.3) |
|
|
| 140 | runcicantic hexagonal ↔ |
(1) (3.10.10) |
(1) (4.4.3) |
(2) (4.6.6) |
(1) (3.6.3.6) |
|
|
| [2] | rectified hexagonal ↔ |
(1) (3.3.3) |
- | (1) (3.3.3) |
(6) (3.6.3.6) |
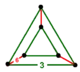 Triangular prism |
 |
| [3] | rectified order-6 tetrahedral ↔ |
(2) (3.3.3.3) |
- | (2) (3.3.3.3) |
(2) (3.3.3.3.3.3) |
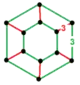 Hexagonal prism |
 |
| [4] | order-6 tetrahedral ↔ |
(4) (4.4.4) |
- | (4) (4.4.4) |
- | |
|
| [8] | cantellated order-6 tetrahedral ↔ |
(1) (3.3.3.3) |
(2) (4.4.6) |
(1) (3.3.3.3) |
(1) (3.6.3.6) |
 |
 |
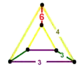| [9] | bitruncated order-6 tetrahedral ↔ |
(1) (3.6.6) |
- | (1) (3.6.6) |
(2) (6.6.6) |
 |
 |
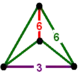| [10] | truncated order-6 tetrahedral ↔ |
(2) (3.10.10) |
- | (2) (3.10.10) |
(1) (3.6.3.6) |
 |
 |
| [14] | cantitruncated order-6 tetrahedral ↔ |
(1) (4.6.6) |
(1) (4.4.6) |
(1) (4.6.6) |
(1) (6.6.6) |
 |
 |
| # | Honeycomb name Coxeter diagram |
Cells by location (and count around each vertex) |
vertex figure | ||||
|---|---|---|---|---|---|---|---|
| 0 |
1 |
0' |
3 |
Alt | |||
| Nonuniform | snub rectified order-6 tetrahedral ↔ |
(3.3.3.3.3) |
(3.3.3.3) |
(3.3.3.3.3) |
 (3.3.3.3.3.3) |
+(3.3.3) |
|
[4,3[3]] family
There are 11 forms, 4 unique, generated by ring permutations of the Coxeter group: [4,3[3]] or . 7 are half symmetry forms of [4,3,6]: ↔ .
| # | Honeycomb name Coxeter diagram |
Cells by location (and count around each vertex) |
vertex figure | Picture | |||
|---|---|---|---|---|---|---|---|
| 0 |
1 |
0' |
3 | ||||
| 141 | alternated order-4 hexagonal ↔ |
- | - | (3.3.3.3) |
(3.3.3.3.3.3) |
(4.6.6) |
|
| 142 | cantic order-4 hexagonal ↔ ↔ |
(1) (3.4.3.4) |
- | (2) (4.6.6) |
(2) (3.6.3.6) |
|
|
| 143 | runcic order-4 hexagonal ↔ |
(1) (4.4.4) |
(1) (4.4.3) |
(3) (3.4.4.4) |
(1) (3.3.3.3.3.3) |
|
|
| 144 | runcicantic order-4 hexagonal ↔ |
(1) (3.8.8) |
(1) (4.4.3) |
(2) (4.6.8) |
(1) (3.6.3.6) |
|
|
| [16] | order-4 hexagonal ↔ |
(4) (4.4.4) |
- | (4) (4.4.4) |
- | |
|
| [17] | rectified order-4 hexagonal ↔ |
(1) (3.3.3.3) |
- | (1) (3.3.3.3) |
(6) (3.6.3.6) |
|
|
| [18] | rectified order-6 cubic ↔ |
(2) (3.4.3.4) |
- | (2) (3.4.3.4) |
(2) (3.3.3.3.3.3) |
|
|
| [21] | bitruncated order-4 hexagonal ↔ |
(1) (4.6.6) |
- | (1) (4.6.6) |
(2) (6.6.6) |
|
|
| [22] | truncated order-6 cubic ↔ |
(2) (3.8.8) |
- | (2) (3.8.8) |
(1) (3.6.3.6) |
 |
 |
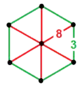| [23] | cantellated order-4 hexagonal ↔ |
(1) (3.4.4.4) |
(2) (4.4.6) |
(1) (3.4.4.4) |
(1) (3.6.3.6) |
 |
 |
| [26] | cantitruncated order-4 hexagonal ↔ |
(1) (4.6.8) |
(1) (4.4.6) |
(1) (4.6.8) |
(1) (6.6.6) |
|
 |
| # | Honeycomb name Coxeter diagram |
Cells by location (and count around each vertex) |
vertex figure | ||||
|---|---|---|---|---|---|---|---|
| 0 |
1 |
0' |
3 |
Alt | |||
| Nonuniform | snub rectified order-4 hexagonal ↔ |
(3.3.3.3.4) |
(3.3.3.3) |
(3.3.3.3.4) |
(3.3.3.3.3.3) |
+(3.3.3) |
|
[5,3[3]] family
There are 11 forms, 4 unique, generated by ring permutations of the Coxeter group: [5,3[3]] or . 7 are half symmetry forms of [5,3,6]: ↔ .
| # | Honeycomb name Coxeter diagram |
Cells by location (and count around each vertex) |
vertex figure | Picture | |||
|---|---|---|---|---|---|---|---|
0 |
1 |
0' |
3 | ||||
| 145 | alternated order-5 hexagonal ↔ |
- | - |  (3.3.3.3.3) |
(3.3.3.3.3.3) |
(3.6.3.6) |
|
| 146 | cantic order-5 hexagonal ↔ |
(1) (3.5.3.5) |
- | (2) (5.6.6) |
(2) (3.6.3.6) |
|
|
| 147 | runcic order-5 hexagonal ↔ |
(1) (5.5.5) |
(1) (4.4.3) |
(3) (3.4.5.4) |
(1) (3.3.3.3.3.3) |
|
|
| 148 | runcicantic order-5 hexagonal ↔ |
(1) (3.10.10) |
(1) (4.4.3) |
(2) (4.6.10) |
(1) (3.6.3.6) |
|
|
| [32] | rectified order-5 hexagonal ↔ |
(1) (3.3.3.3.3) |
- | (1) (3.3.3.3.3) |
(6) (3.6.3.6) |
 |
 |
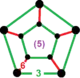| [33] | rectified order-6 dodecahedral ↔ |
(2) (3.5.3.5) |
- | (2) (3.5.3.5) |
(2) (3.3.3.3.3.3) |
 |
 |
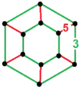| [34] | Order-5 hexagonal ↔ |
(4) (5.5.5) |
- | (4) (5.5.5) |
- |  |
|
| [35] | truncated order-6 dodecahedral ↔ |
(2) (3.10.10) |
- | (2) (3.10.10) |
(1) (3.6.3.6) |
 |
 |
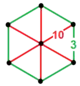| [38] | cantellated order-5 hexagonal ↔ |
(1) (3.4.5.4) |
(2) (6.4.4) |
(1) (3.4.5.4) |
(1) (3.6.3.6) |
 |
 |
| [39] | bitruncated order-5 hexagonal ↔ |
(1) (5.6.6) |
- | (1) (5.6.6) |
(2) (6.6.6) |
 |
 |
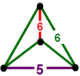| [44] | cantitruncated order-5 hexagonal ↔ |
(1) (4.6.10) |
(1) (6.4.4) |
(1) (4.6.10) |
(1) (6.6.6) |
 |
 |
| # | Honeycomb name Coxeter diagram |
Cells by location (and count around each vertex) |
vertex figure | Picture | ||||
|---|---|---|---|---|---|---|---|---|
| 0 |
1 |
0' |
3 |
Alt | ||||
| Nonuniform | snub rectified order-5 hexagonal ↔ |
(3.3.3.3.5) |
(3.3.3) |
(3.3.3.3.5) |
(3.3.3.3.3.3) |
+(3.3.3) |
||
[6,3[3]] family
There are 11 forms, 4 unique, generated by ring permutations of the Coxeter group: [6,3[3]] or . 7 are half symmetry forms of [6,3,6]: ↔ .
| # | Honeycomb name Coxeter diagram |
Cells by location (and count around each vertex) |
vertex figure | Picture | |||
|---|---|---|---|---|---|---|---|
| 0 |
1 |
0' |
3 | ||||
| 149 | runcic order-6 hexagonal ↔ |
(1) (6.6.6) |
(1) (4.4.3) |
(3) (3.4.6.4) |
(1) (3.3.3.3.3.3) |
|
|
| 150 | runcicantic order-6 hexagonal ↔ |
(1) (3.12.12) |
(1) (4.4.3) |
(2) (4.6.12) |
(1) (3.6.3.6) |
|
|
| [1] | hexagonal ↔ ↔ ↔ |
(1) (6.6.6) |
- | (1) (6.6.6) |
(2) (6.6.6) |
 |
|
| [46] | order-6 hexagonal ↔ |
(4) (6.6.6) |
- | (4) (6.6.6) |
- | |
|
| [47] | rectified order-6 hexagonal ↔ |
(2) (3.6.3.6) |
- | (2) (3.6.3.6) |
(2) (3.3.3.3.3.3) |
|
|
| [47] | rectified order-6 hexagonal ↔ |
(1) (3.3.3.3.3.3) |
- | (1) (3.3.3.3.3.3) |
(6) (3.6.3.6) |
|
|
| [48] | truncated order-6 hexagonal ↔ |
(2) (3.12.12) |
- | (2) (3.12.12) |
(1) (3.3.3.3.3.3) |
|
|
| [49] | cantellated order-6 hexagonal ↔ |
(1) (3.4.6.4) |
(2) (6.4.4) |
(1) (3.4.6.4) |
(1) (3.6.3.6) |
|
|
| [51] | cantitruncated order-6 hexagonal ↔ |
(1) (4.6.12) |
(1) (6.4.4) |
(1) (4.6.12) |
(1) (6.6.6) |
|
|
| [54] | triangular tiling honeycomb ( ↔ ) = |
- | - | (3.3.3.3.3.3) |
(3.3.3.3.3.3) |
(6.6.6) |
|
| [55] | cantic order-6 hexagonal ( ↔ ) = |
(1) (3.6.3.6) |
- | (2) (6.6.6) |
(2) (3.6.3.6) |
|
|
| # | Honeycomb name Coxeter diagram |
Cells by location (and count around each vertex) |
vertex figure | Picture | ||||
|---|---|---|---|---|---|---|---|---|
| 0 |
1 |
0' |
3 |
Alt | ||||
| [54] | triangular tiling honeycomb ( ↔ ↔ ) = |
|
- | |
- | |
(6.6.6) |
|
| [137] | alternated hexagonal ( ↔ ) = ( ↔ ) |
|
- | |
|
+(3.6.6) |
(3.6.6) |
|
| [47] | rectified order-6 hexagonal ↔ ↔ ↔ |
(3.6.3.6) |
- | (3.6.3.6) |
(3.3.3.3.3.3) |
|
| |
| [55] | cantic order-6 hexagonal ( ↔ ) = ( ↔ ) = |
(1) (3.6.3.6) |
- | (2) (6.6.6) |
(2) (3.6.3.6) |
|
| |
| Nonuniform | snub rectified order-6 hexagonal ↔ |
(3.3.3.3.6) |
(3.3.3.3) |
(3.3.3.3.6) |
(3.3.3.3.3.3) |
+(3.3.3) |
||
Multicyclic graphs
[3[ ]×[ ]] family
There are 8 forms, 1 unique, generated by ring permutations of the Coxeter group: . Two are duplicated as ↔ , two as ↔ , and three as ↔ .
| # | Honeycomb name Coxeter diagram |
Cells by location (and count around each vertex) |
Vertex figure | Picture | |||
|---|---|---|---|---|---|---|---|
| 0 |
1 |
2 |
3 | ||||
| 151 | Quarter order-4 hexagonal ↔ |
|
|
|
|
|
|
| [17] | rectified order-4 hexagonal ↔ ↔ ↔ |
|
|
|
 |
(4.4.4) |
|
| [18] | rectified order-6 cubic ↔ ↔ ↔ |
 |
|
|
|
(6.4.4) |
|
| [21] | bitruncated order-6 cubic ↔ ↔ ↔ |
|
|
|
|
|
|
| [87] | alternated order-6 cubic ↔ ↔ |
- | |
|
|
(3.6.3.6) |
|
| [88] | cantic order-6 cubic ↔ ↔ |
|
|
|
|
|
|
| [141] | alternated order-4 hexagonal ↔ ↔ |
|
- | |
|
(4.6.6) |
|
| [142] | cantic order-4 hexagonal ↔ ↔ |
|
|
|
|
|
|
| # | Honeycomb name Coxeter diagram |
Cells by location (and count around each vertex) |
Vertex figure | Picture | ||||
|---|---|---|---|---|---|---|---|---|
| 0 |
1 |
2 |
3 |
Alt | ||||
| Nonuniform | bisnub order-6 cubic ↔ |
|
|
|
|
irr. {3,3} |
|
|
[3[3,3]] family
There are 4 forms, 0 unique, generated by ring permutations of the Coxeter group: . They are repeated in four families: 
↔ (index 2 subgroup),
↔ (index 4 subgroup),
↔ (index 6 subgroup), and
↔ (index 24 subgroup).
| # | Name Coxeter diagram |
0 | 1 | 2 | 3 | vertex figure | Picture |
|---|---|---|---|---|---|---|---|
| [1] | hexagonal ↔ |
|
|
|
|
{3,3} |
|
| [47] | rectified order-6 hexagonal ↔ |
|
|
|
|
t{2,3} |
|
| [54] | triangular tiling honeycomb ( ↔ ) = |
|
- | |
 |
t{3[3]} |
|
| [55] | rectified triangular ↔ |
|
|
|
|
t{2,3} |
|
| # | Name Coxeter diagram |
0 | 1 | 2 | 3 | Alt | vertex figure | Picture |
|---|---|---|---|---|---|---|---|---|
| [137] | alternated hexagonal ( ↔ ) = |
s{3[3]} |
s{3[3]} |
s{3[3]} |
s{3[3]} |
{3,3} |
(4.6.6) |
Summary enumerations by family
Linear graphs
| Group | Extended symmetry |
Honeycombs | Chiral extended symmetry |
Alternation honeycombs | ||
|---|---|---|---|---|---|---|
[4,4,3] |
[4,4,3] | 15 | | | | | | | | | | | | | |
[1+,4,1+,4,3+] | (6) | | |
| [4,4,3]+ | (1) | | ||||
[4,4,4] |
[4,4,4] | 3 | | |
[1+,4,1+,4,1+,4,1+] | (3) | |
| [4,4,4] ↔ |
(3) | | |
[1+,4,1+,4,1+,4,1+] | (3) | | |
| [2+[4,4,4]] | 3 | | | |
[2+[(4,4+,4,2+)]] | (2) | | |
| [2+[4,4,4]]+ | (1) | | ||||
[6,3,3] |
[6,3,3] | 15 | | | | | | | | | | | | | |
[1+,6,(3,3)+] | (2) | (↔ ) |
| [6,3,3]+ | (1) | | ||||
[6,3,4] |
[6,3,4] | 15 | | | | | | | | | | | | | |
[1+,6,3+,4,1+] | (6) | | |
| [6,3,4]+ | (1) | | ||||
[6,3,5] |
[6,3,5] | 15 | | | | | | | | | | | | | |
[1+,6,(3,5)+] | (2) | (↔ ) |
| [6,3,5]+ | (1) | | ||||
[3,6,3] |
[3,6,3] | 5 | | | | |
|||
| [3,6,3] ↔ | (1) | |
[2+[3+,6,3+]] | (1) | | |
| [2+[3,6,3]] | 3 | | |
[2+[3,6,3]]+ | (1) | | |
[6,3,6] |
[6,3,6] | 6 | | | | |
[1+,6,3+,6,1+] | (2) | (↔ ) |
| [2+[6,3,6]] ↔ | (1) | |
[2+[(6,3+,6,2+)]] | (2) | | |
| [2+[6,3,6]] | 2 | | |
| |||
| [2+[6,3,6]]+ | (1) | | ||||
Tridental graphs
| Group | Extended symmetry |
Honeycombs | Chiral extended symmetry |
Alternation honeycombs | ||
|---|---|---|---|---|---|---|
[6,31,1] | [6,31,1] | 4 | | | |
|||
| [1[6,31,1]]=[6,3,4] ↔ | (7) | | | | | | | |
[1[1+,6,31,1]]+ | (2) | (↔ ) | |
| [1[6,31,1]]+=[6,3,4]+ | (1) | | ||||
[3,41,1] | [3,41,1] | 4 | | | |
[3+,41,1]+ | (2) |  ↔ |
| [1[3,41,1]]=[3,4,4] ↔ | (7) | | | | | | | |
[1[3+,41,1]]+ | (2) | | |
| [1[3,41,1]]+ | (1) | | ||||
[41,1,1] | [41,1,1] | 0 | (none) | |||
| [1[41,1,1]]=[4,4,4] ↔ | (4) | | | |
[1[1+,4,1+,41,1]]+=[(4,1+,4,1+,4,2+)] | (4) | | | |
[3[41,1,1]]=[4,4,3] ↔ | (3) | | | |
[3[1+,41,1,1]]+=[1+,4,1+,4,3+] | (2) | (↔ ) | |
| [3[41,1,1]]+=[4,4,3]+ | (1) | | ||||
Cyclic graphs
| Group | Extended symmetry |
Honeycombs | Chiral extended symmetry |
Alternation honeycombs | ||
|---|---|---|---|---|---|---|
[(4,4,4,3)] |
[(4,4,4,3)] | 6 | | | | | |
[(4,1+,4,1+,4,3+)] | (2) | ↔ |
[2+[(4,4,4,3)]] | 3 | | | |
[2+[(4,4+,4,3+)]] | (2) | | |
| [2+[(4,4,4,3)]]+ | (1) | | ||||
[4[4]] |
[4[4]] | (none) | ||||
| [2+[4[4]]] | 1 | |
[2+[(4+,4)[2]]] | (1) | | |
| [1[4[4]]]=[4,41,1] ↔ | (2) | |
[(1+,4)[4]] | (2) | ↔ | |
| [2[4[4]]]=[4,4,4] ↔ | (1) | |
[2+[(1+,4,4)[2]]] | (1) | | |
| [(2+,4)[4[4]]]=[2+[4,4,4]] = | (1) | |
[(2+,4)[4[4]]]+ = [2+[4,4,4]]+ |
(1) | | |
[(6,3,3,3)] |
[(6,3,3,3)] | 6 | | | | | |
|||
| [2+[(6,3,3,3)]] | 3 | | |
[2+[(6,3,3,3)]]+ | (1) | | |
[(3,4,3,6)] |
[(3,4,3,6)] | 6 | | | | | |
[(3+,4,3+,6)] | (1) | |
| [2+[(3,4,3,6)]] | 3 | | |
[2+[(3,4,3,6)]]+ | (1) | | |
[(3,5,3,6)] |
[(3,5,3,6)] | 6 | | | | | |
|||
| [2+[(3,5,3,6)]] | 3 | | |
[2+[(3,5,3,6)]]+ | (1) | | |
[(3,6)[2]] |
[(3,6)[2]] | 2 | |
|||
[2+[(3,6)[2]]] | 1 | |
||||
| [2+[(3,6)[2]]] | 1 | |
||||
[2+[(3,6)[2]]] = | (1) | |
[2+[(3+,6)[2]]] | (1) | | |
| [(2,2)+[(3,6)[2]]] | 1 | |
[(2,2)+[(3,6)[2]]]+ | (1) | | |
| Group | Extended symmetry |
Honeycombs | Chiral extended symmetry |
Alternation honeycombs | ||
|---|---|---|---|---|---|---|
[(3,3,4,4)] |
[(3,3,4,4)] | 4 | | | |
|||
| [1[(4,4,3,3)]]=[3,41,1] ↔ | (7) | | | | | | | |
[1[(3,3,4,1+,4)]]+ = [3+,41,1]+ | (2) | (= ) | |
| [1[(3,3,4,4)]]+ = [3,41,1]+ | (1) | | ||||
[3[ ]x[ ]] |
[3[ ]x[ ]] | 1 | |
|||
| [1[3[ ]x[ ]]]=[6,31,1] ↔ | (2) | |
||||
| [1[3[ ]x[ ]]]=[4,3[3]] ↔ | (2) | |
||||
| [2[3[ ]x[ ]]]=[6,3,4] ↔ | (3) | | |
[2[3[ ]x[ ]]]+ =[6,3,4]+ | (1) | | |
[3[3,3]]  |
[3[3,3]] | 0 | (none) | |||
| [1[3[3,3]]]=[6,3[3]] ↔ | 0 | (none) | ||||
| [3[3[3,3]]]=[3,6,3] ↔ | (2) | |
||||
| [2[3[3,3]]]=[6,3,6] ↔ | (1) | |
||||
| [(3,3)[3[3,3]]]=[6,3,3] = | (1) | |
[(3,3)[3[3,3]]]+ = [6,3,3]+ | (1) | | |
Loop-n-tail graphs
Symmetry in these graphs can be doubled by adding a mirror: [1[n,3[3]]] = [n,3,6]. Therefore ring-symmetry graphs are repeated in the linear graph families.
| Group | Extended symmetry |
Honeycombs | Chiral extended symmetry |
Alternation honeycombs | ||
|---|---|---|---|---|---|---|
[3,3[3]] | [3,3[3]] | 4 | | | |
|||
| [1[3,3[3]]]=[3,3,6] ↔ | (7) | | | | | | |
[1[3,3[3]]]+ = [3,3,6]+ | (1) | | |
[4,3[3]] | [4,3[3]] | 4 | | | |
|||
| [1[4,3[3]]]=[4,3,6] ↔ | (7) | | | | | | | |
[1+,4,(3[3])+] | (2) | ↔ | |
| [4,3[3]]+ | (1) | | ||||
[5,3[3]] | [5,3[3]] | 4 | | | |
|||
| [1[5,3[3]]]=[5,3,6] ↔ | (7) | | | | | | |
[1[5,3[3]]]+ = [5,3,6]+ | (1) | | |
[6,3[3]] | [6,3[3]] | 2 | |
|||
| [6,3[3]] = | (2) | ( = ) |
||||
| [(3,3)[1+,6,3[3]]]=[6,3,3] ↔ ↔ | (1) | |
[(3,3)[1+,6,3[3]]]+ | (1) | | |
| [1[6,3[3]]]=[6,3,6] ↔ | (6) | | | | | | |
[3[1+,6,3[3]]]+ = [3,6,3]+ | (1) | ↔ (= ) | |
| [1[6,3[3]]]+ = [6,3,6]+ | (1) | | ||||
See also
References
- James E. Humphreys, Reflection Groups and Coxeter Groups, Cambridge studies in advanced mathematics, 29 (1990)
- The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN 99-35678, ISBN 0-486-40919-8 (Chapter 10, Regular Honeycombs in Hyperbolic Space)
- Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
- Jeffrey R. Weeks The Shape of Space, 2nd edition ISBN 0-8247-0709-5 (Chapter 16-17: Geometries on Three-manifolds I,II)
- Coxeter Decompositions of Hyperbolic Tetrahedra, arXiv/PDF, A. Felikson, December 2002
- C. W. L. Garner, Regular Skew Polyhedra in Hyperbolic Three-Space Can. J. Math. 19, 1179-1186, 1967. PDF
- Norman Johnson, Geometries and Transformations, (2018) Chapters 11,12,13
- N. W. Johnson, R. Kellerhals, J. G. Ratcliffe, S. T. Tschantz, The size of a hyperbolic Coxeter simplex, Transformation Groups (1999), Volume 4, Issue 4, pp 329–353
- N.W. Johnson, R. Kellerhals, J.G. Ratcliffe,S.T. Tschantz, Commensurability classes of hyperbolic Coxeter groups, (2002) H3: p130.
- Klitzing, Richard. "Hyperbolic honeycombs H3 paracompact".
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.