Order-4 octahedral honeycomb

The order-4 octahedral honeycomb is a regular paracompact honeycomb in hyperbolic 3-space. It is paracompact because it has infinite vertex figures, with all vertices as ideal points at infinity. Given by Schläfli symbol {3,4,4}, it has four ideal octahedra around each edge, and infinite octahedra around each vertex in a square tiling vertex figure.[1]

Order-4 octahedral honeycomb
Perspective projection view within Poincaré disk model
Type	Hyperbolic regular honeycomb Paracompact uniform honeycomb
Schläfli symbols	{3,4,4} {3,4^1,1}
Coxeter diagrams	↔ ↔ ↔
Cells	{3,4}
Faces	triangle {3}
Edge figure	square {4}
Vertex figure	square tiling, {4,4}
Dual	Square tiling honeycomb, {4,4,3}
Coxeter groups	${\overline {R}}_{3}$ , [3,4,4] ${\overline {O}}_{3}$ , [3,4^1,1]
Properties	Regular

A geometric honeycomb is a space-filling of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions.

Honeycombs are usually constructed in ordinary Euclidean ("flat") space, like the convex uniform honeycombs. They may also be constructed in non-Euclidean spaces, such as hyperbolic uniform honeycombs. Any finite uniform polytope can be projected to its circumsphere to form a uniform honeycomb in spherical space.

Symmetry

A half symmetry construction, [3,4,4,1⁺], exists as {3,4^1,1}, with two alternating types (colors) of octahedral cells: ↔ .

A second half symmetry is [3,4,1⁺,4]: ↔ .

A higher index sub-symmetry, [3,4,4^*], which is index 8, exists with a pyramidal fundamental domain, [((3,∞,3)),((3,∞,3))]: .

This honeycomb contains and that tile 2-hypercycle surfaces, which are similar to the paracompact infinite-order triangular tilings and , respectively:

Related polytopes and honeycombs

The order-4 octahedral honeycomb is a regular hyperbolic honeycomb in 3-space, and is one of eleven regular paracompact honeycombs.

11 paracompact regular honeycombs
{6,3,3}	{6,3,4}	{6,3,5}	{6,3,6}	{4,4,3}	{4,4,4}
{3,3,6}	{4,3,6}	{5,3,6}	{3,6,3}	{3,4,4}

There are fifteen uniform honeycombs in the [3,4,4] Coxeter group family, including this regular form.

[4,4,3] family honeycombs
{4,4,3}	r{4,4,3}	t{4,4,3}	rr{4,4,3}	t_0,3{4,4,3}	tr{4,4,3}	t_0,1,3{4,4,3}	t_0,1,2,3{4,4,3}


{3,4,4}	r{3,4,4}	t{3,4,4}	rr{3,4,4}	2t{3,4,4}	tr{3,4,4}	t_0,1,3{3,4,4}	t_0,1,2,3{3,4,4}

It is a part of a sequence of honeycombs with a square tiling vertex figure:

{p,4,4} honeycombs
Space	E³	H³
Form	Affine	Paracompact		Noncompact
Name	{2,4,4}	{3,4,4}	{4,4,4}	{5,4,4}	{6,4,4}	..{∞,4,4}
Coxeter
Image
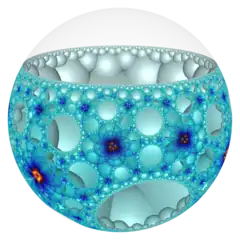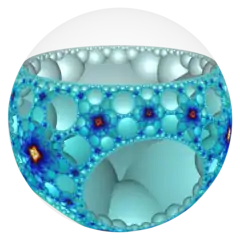Cells	{2,4}	{3,4}	{4,4}	{5,4}	{6,4}	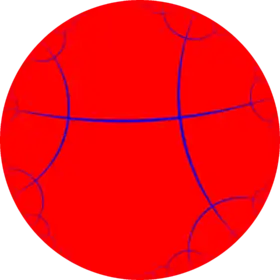{∞,4}

It a part of a sequence of regular polychora and honeycombs with octahedral cells:

{3,4,p} polytopes
Space	S³	H³
Form	Finite	Paracompact	Noncompact
Name	{3,4,3}	{3,4,4}	{3,4,5}	{3,4,6}	{3,4,7}	{3,4,8}	... {3,4,∞}
Image
Vertex figure	{4,3}	{4,4}	{4,5}	{4,6}	{4,7}	{4,8}	{4,∞}

Rectified order-4 octahedral honeycomb

Rectified order-4 octahedral honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbols	r{3,4,4} or t₁{3,4,4}
Coxeter diagrams	↔ ↔ ↔
Cells	r{4,3} {4,4}
Faces	triangle {3} square {4}
Vertex figure	square prism
Coxeter groups	${\overline {R}}_{3}$ , [3,4,4] ${\overline {O}}_{3}$ , [3,4^1,1]
Properties	Vertex-transitive, edge-transitive

The rectified order-4 octahedral honeycomb, t₁{3,4,4}, has cuboctahedron and square tiling facets, with a square prism vertex figure.

Truncated order-4 octahedral honeycomb

Truncated order-4 octahedral honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbols	t{3,4,4} or t_0,1{3,4,4}
Coxeter diagrams	↔ ↔ ↔
Cells	t{3,4} {4,4}
Faces	square {4} hexagon {6}
Vertex figure	square pyramid
Coxeter groups	${\overline {R}}_{3}$ , [3,4,4] ${\overline {O}}_{3}$ , [3,4^1,1]
Properties	Vertex-transitive

The truncated order-4 octahedral honeycomb, t_0,1{3,4,4}, has truncated octahedron and square tiling facets, with a square pyramid vertex figure.

Bitruncated order-4 octahedral honeycomb

The bitruncated order-4 octahedral honeycomb is the same as the bitruncated square tiling honeycomb.

Cantellated order-4 octahedral honeycomb

Cantellated order-4 octahedral honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbols	rr{3,4,4} or t_0,2{3,4,4} s₂{3,4,4}
Coxeter diagrams	↔
Cells	rr{3,4} {}x4 r{4,4}
Faces	triangle {3} square {4}
Vertex figure	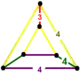wedge
Coxeter groups	${\overline {R}}_{3}$ , [3,4,4] ${\overline {O}}_{3}$ , [3,4^1,1]
Properties	Vertex-transitive

The cantellated order-4 octahedral honeycomb, t_0,2{3,4,4}, has rhombicuboctahedron, cube, and square tiling facets, with a wedge vertex figure.

Cantitruncated order-4 octahedral honeycomb

Cantitruncated order-4 octahedral honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbols	tr{3,4,4} or t_0,1,2{3,4,4}
Coxeter diagrams	↔
Cells	tr{3,4} {}x{4} t{4,4}
Faces	square {4} hexagon {6} octagon {8}
Vertex figure	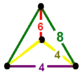mirrored sphenoid
Coxeter groups	${\overline {R}}_{3}$ , [3,4,4] ${\overline {O}}_{3}$ , [3,4^1,1]
Properties	Vertex-transitive

The cantitruncated order-4 octahedral honeycomb, t_0,1,2{3,4,4}, has truncated cuboctahedron, cube, and truncated square tiling facets, with a mirrored sphenoid vertex figure.

Runcinated order-4 octahedral honeycomb

The runcinated order-4 octahedral honeycomb is the same as the runcinated square tiling honeycomb.

Runcitruncated order-4 octahedral honeycomb

Runcitruncated order-4 octahedral honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbols	t_0,1,3{3,4,4}
Coxeter diagrams	↔
Cells	t{3,4} {6}x{} rr{4,4}
Faces	square {4} hexagon {6} octagon {8}
Vertex figure	square pyramid
Coxeter groups	${\overline {R}}_{3}$ , [3,4,4]
Properties	Vertex-transitive

The runcitruncated order-4 octahedral honeycomb, t_0,1,3{3,4,4}, has truncated octahedron, hexagonal prism, and square tiling facets, with a square pyramid vertex figure.

Runcicantellated order-4 octahedral honeycomb

The runcicantellated order-4 octahedral honeycomb is the same as the runcitruncated square tiling honeycomb.

Omnitruncated order-4 octahedral honeycomb

The omnitruncated order-4 octahedral honeycomb is the same as the omnitruncated square tiling honeycomb.

Snub order-4 octahedral honeycomb

Snub order-4 octahedral honeycomb
Type	Paracompact scaliform honeycomb
Schläfli symbols	s{3,4,4}
Coxeter diagrams	↔ ↔ ↔
Cells	square tiling icosahedron square pyramid
Faces	triangle {3} square {4}
Vertex figure
Coxeter groups	[4,4,3⁺] [4^1,1,3⁺] [(4,4,(3,3)⁺)]
Properties	Vertex-transitive

The snub order-4 octahedral honeycomb, s{3,4,4}, has Coxeter diagram . It is a scaliform honeycomb, with square pyramid, square tiling, and icosahedron facets.

References

Coxeter The Beauty of Geometry, 1999, Chapter 10, Table III

Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN 99-35678, ISBN 0-486-40919-8 (Chapter 10, Regular Honeycombs in Hyperbolic Space) Table III
Jeffrey R. Weeks The Shape of Space, 2nd edition ISBN 0-8247-0709-5 (Chapter 16-17: Geometries on Three-manifolds I,II)
Norman Johnson Uniform Polytopes, Manuscript
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- N.W. Johnson: Geometries and Transformations, (2015) Chapter 13: Hyperbolic Coxeter groups
- Norman W. Johnson and Asia Ivic Weiss Quadratic Integers and Coxeter Groups PDF Can. J. Math. Vol. 51 (6), 1999 pp. 1307–1336

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Coxeter The Beauty of Geometry, 1999, Chapter 10, Table III