Weak isospin
In particle physics, weak isospin is a quantum number relating to the weak interaction, and parallels the idea of isospin under the strong interaction. Weak isospin is usually given the symbol or with the third component written as , , , or .[lower-alpha 1] It can be understood as the eigenvalue of a charge operator.
| Flavour in particle physics |
|---|
| Flavour quantum numbers |
|
| Related quantum numbers |
|
| Combinations |
|
| Flavour mixing |
The weak isospin conservation law relates to the conservation of ; all weak interactions must conserve . It is also conserved by the electromagnetic and strong interactions. However, one of the interactions is with the Higgs field. Since the Higgs field vacuum expectation value is nonzero, particles interact with this field all the time even in vacuum. This changes their weak isospin (and weak hypercharge). Only a specific combination of them, (electric charge), is conserved. is more important than T and often the term "weak isospin" refers to the "3rd component of weak isospin".
Relation with chirality
Fermions with negative chirality (also called "left-handed" fermions) have and can be grouped into doublets with that behave the same way under the weak interaction. By convention, electrically charged fermions are assigned with the same sign as their electric charge.[lower-alpha 2] For example, up-type quarks (u, c, t) have and always transform into down-type quarks (d, s, b), which have , and vice versa. On the other hand, a quark never decays weakly into a quark of the same . Something similar happens with left-handed leptons, which exist as doublets containing a charged lepton (
e−
,
μ−
,
τ−
) with and a neutrino (
ν
e,
ν
μ,
ν
τ) with . In all cases, the corresponding anti-fermion has reversed chirality ("right-handed" antifermion) and reversed sign .
Fermions with positive chirality ("right-handed" fermions) and anti-fermions with negative chirality ("left-handed" anti-fermions) have and form singlets that do not undergo weak interactions.
The electric charge, , is related to weak isospin, , and weak hypercharge, , by
- .
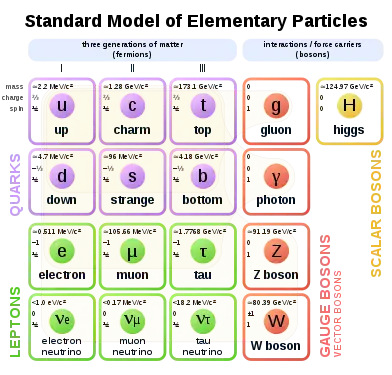
| Generation 1 | Generation 2 | Generation 3 | ||||||
|---|---|---|---|---|---|---|---|---|
| Fermion | Symbol | Weak isospin |
Fermion | Symbol | Weak isospin |
Fermion | Symbol | Weak isospin |
| Electron neutrino | Muon neutrino | Tau neutrino | ||||||
| Electron | Muon | Tau | ||||||
| Up quark | Charm quark | Top quark | ||||||
| Down quark | Strange quark | Bottom quark | ||||||
| All of the above left-handed (regular) particles have corresponding right-handed anti-particles with equal and opposite weak isospin. | ||||||||
| All right-handed (regular) particles and left-handed antiparticles have weak isospin of 0. | ||||||||
Weak isospin and the W bosons
The symmetry associated with weak isospin is SU(2) and requires gauge bosons with (
W+
,
W−
and
W0
) to mediate transformations between fermions with half-integer weak isospin charges. implies that
W
bosons have three different values of :
W+
boson is emitted in transitions → .
W0
boson would be emitted in weak interactions where does not change, such as neutrino scattering.
W−
boson is emitted in transitions → .
Under electroweak unification, the
W0
boson mixes with the weak hypercharge gauge boson
B
, resulting in the observed
Z0
boson and the photon of quantum electrodynamics; the resulting
Z0
and the photon both have weak isospin = 0.
The sum of −isospin and +charge is zero for each of the bosons, consequently, all the electroweak bosons have weak hypercharge , so unlike gluons of the color force, the electroweak bosons are unaffected by the force they mediate.
See also
Footnotes
- Regarding ambiguous notation, is also used to represent the ‘normal’ (strong force) isospin, same for its third component a.k.a. or . is also used as the symbol for the Topness quantum number. This article uses and for weak isospin and its projection.
- Lacking a distinguishing electric charge, neutrinos and antineutrinos are assigned the opposite their corresponding charged lepton; hence, all left-handed neutrinos are paired with negatively charged left-handed leptons with so those neutrinos have From anti-particle charge-reversal, all right-handed antineutrinos have since they are paired with positively charged anti-leptons.
References
- Baez, John C.; Huerta, John (2009). "The Algebra of Grand Unified Theories". Bull. Am. Math. Soc. 0904: 483–552. arXiv:0904.1556. Bibcode:2009arXiv0904.1556B. doi:10.1090/s0273-0979-10-01294-2. Retrieved 15 October 2013.