Weinberg angle

The Weinberg angle or weak mixing angle[1] is a parameter in the Weinberg–Salam theory of the electroweak interaction, part of the Standard Model of particle physics, and is usually denoted as θ_W. It is the angle by which spontaneous symmetry breaking rotates the original
W⁰
and B⁰ vector boson plane, producing as a result the
Z⁰
boson, and the photon.[2]

${\displaystyle {\begin{pmatrix}\gamma \\Z^{0}\end{pmatrix}}={\begin{pmatrix}\cos \theta _{\text{W}}&\sin \theta _{\text{W}}\\-\sin \theta _{\text{W}}&\cos \theta _{\text{W}}\end{pmatrix}}{\begin{pmatrix}B^{0}\\W^{0}\end{pmatrix}}}$

Weinberg angle θ_W, and relation between couplings g, g', and e=gsin θ_W. Adapted from T D Lee's book Particle Physics and Introduction to Field Theory (1981).

The pattern of weak isospin, T₃, and weak hypercharge, Y_W, of the known elementary particles, showing electric charge, Q, along the Weinberg angle. The neutral Higgs field (circled) breaks the electroweak symmetry and interacts with other particles to give them mass. Three components of the Higgs field become part of the massive W and Z bosons.

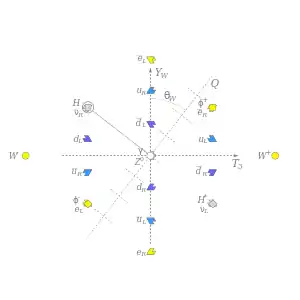
It also gives the relationship between the masses of the W and Z bosons (denoted as m_W and m_Z),

${\displaystyle m_{\text{Z}}={\frac {m_{\text{W}}}{\cos \theta _{\text{W}}}}~.}$

The angle can be expressed in terms of the ${\displaystyle \mathrm {SU} (2)_{L}}$ and ${\displaystyle \mathrm {U} (1)_{Y}}$ couplings (weak isospin g and weak hypercharge g′, respectively),

${\displaystyle \cos \theta _{\text{W}}={\frac {g}{\sqrt {g^{2}+g'^{2}}}}\qquad }$ and ${\displaystyle \qquad \sin \theta _{\text{W}}={\frac {g'}{\sqrt {g^{2}+g'^{2}}}}~.}$

The electric charge is then expressible in terms of it, e = g sin θ_W = g′ cos θ_W; see the Figure.

As the value of the mixing angle is currently determined empirically, it has been mathematically defined as[3]

${\displaystyle \cos \theta _{\text{W}}={\frac {m_{\text{W}}}{m_{\text{Z}}}}~.}$

The value of θ_W varies as a function of the momentum transfer, Q, at which it is measured. This variation, or 'running', is a key prediction of the electroweak theory. The most precise measurements have been carried out in electron–positron collider experiments at a value of Q = 91.2 GeV/c, corresponding to the mass of the Z boson, m_Z.

In practice the quantity sin²θ_W is more frequently used. The 2004 best estimate of sin²θ_W, at Q = 91.2 GeV/c, in the MS scheme is 0.23120 ± 0.00015, which averages over measurements made in different processes and at different detectors. Atomic parity violation experiments yield values for sin²θ_W at smaller values of Q, below 0.01 GeV/c, but with much lower precision. In 2005 results were published from a study of parity violation in Møller scattering in which a value of sin²θ_W = 0.2397 ± 0.0013 was obtained at Q = 0.16 GeV/c, establishing experimentally the 'running' of the weak mixing angle. These values correspond to a Weinberg angle of ~30°. LHCb measured in 7 and 8 TeV proton-proton collisions an effective angle of sin²(θ_W^eff) = 0.23142, though the value of Q for this measurement is determined by the partonic collision energy, which is close to the Z boson mass.

CODATA 2018[4] gives the value

${\displaystyle \sin ^{2}\theta _{\text{W}}=1-(m_{\text{W}}/m_{\text{Z}})^{2}=0.22290(30)}$.

Note, however, that the specific value of the angle is not a prediction of the standard model: it is an open, unfixed parameter. However, it is constrained and predicted through other measurements of Standard Model quantities. At this time, there is no generally accepted theory that explains why the measured value is what it is.