Activation energy

Although less commonly used, activation energy also applies to nuclear reactions[4][5] and various other physical phenomena.[6][7][8][9]

The Arrhenius equation gives the quantitative basis of the relationship between the activation energy and the rate at which a reaction proceeds. From the equation, the activation energy can be found through the relation

${\displaystyle k=Ae^{{-E_{\textrm {a}}}/{(RT)}}}$

where A is the pre-exponential factor for the reaction, R is the universal gas constant, T is the absolute temperature (usually in kelvins), and k is the reaction rate coefficient. Even without knowing A, E_a can be evaluated from the variation in reaction rate coefficients as a function of temperature (within the validity of the Arrhenius equation).

At a more advanced level, the net Arrhenius activation energy term from the Arrhenius equation is best regarded as an experimentally determined parameter that indicates the sensitivity of the reaction rate to temperature. There are two objections to associating this activation energy with the threshold barrier for an elementary reaction. First, it is often unclear as to whether or not reaction does proceed in one step; threshold barriers that are averaged out over all elementary steps have little theoretical value. Second, even if the reaction being studied is elementary, a spectrum of individual collisions contributes to rate constants obtained from bulk ('bulb') experiments involving billions of molecules, with many different reactant collision geometries and angles, different translational and (possibly) vibrational energies—all of which may lead to different microscopic reaction rates.

Example of an enzyme-catalysed exothermic reaction

The relationship between activation energy (${\displaystyle E_{\textrm {a}}}$) and enthalpy of formation (ΔH) with and without a catalyst, plotted against the reaction coordinate. The highest energy position (peak position) represents the transition state. With the catalyst, the energy required to enter transition state decreases, thereby decreasing the energy required to initiate the reaction.

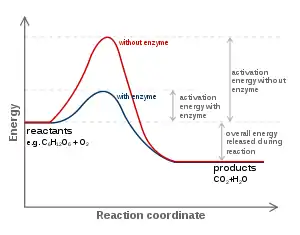
A substance that modifies the transition state to lower the activation energy is termed a catalyst; a catalyst composed only of protein and (if applicable) small molecule cofactors is termed an enzyme. A catalyst increases the rate of reaction without being consumed in the reaction.[10] In addition, the catalyst lowers the activation energy, but it does not change the energies of the original reactants or products, and so does not change equilibrium.[11] Rather, the reactant energy and the product energy remain the same and only the activation energy is altered (lowered).

A catalyst is able to reduce the activation energy by forming a transition state in a more favorable manner. Catalysts, by nature, create a more "comfortable" fit for the substrate of a reaction to progress to a transition state. This is possible due to a release of energy that occurs when the substrate binds to the active site of a catalyst. This energy is known as Binding Energy. Upon binding to a catalyst, substrates partake in numerous stabilizing forces while within the active site (i.e. Hydrogen bonding, van der Waals forces). Specific and favorable bonding occurs within the active site until the substrate forms to become the high-energy transition state. Forming the transition state is more favorable with the catalyst because the favorable stabilizing interactions within the active site release energy. A chemical reaction is able to manufacture a high-energy transition state molecule more readily when there is a stabilizing fit within the active site of a catalyst. The binding energy of a reaction is this energy released when favorable interactions between substrate and catalyst occur. The binding energy released assists in achieving the unstable transition state. Reactions otherwise without catalysts need a higher input of energy to achieve the transition state. Non-catalyzed reactions do not have free energy available from active site stabilizing interactions, such as catalytic enzyme reactions.[12]

In the Arrhenius equation, the term activation energy (E_a) is used to describe the energy required to reach the transition state, and the exponential relationship k = A exp(-E_a/RT) holds. In transition state theory, a more sophisticated model of the relationship between reaction rates and the transition state, a superficially similar mathematical relationship, the Eyring equation, is used to describe the rate of a reaction: k = (k_BT / h) exp(–ΔG^‡ / RT). However, instead of modeling the temperature dependence of reaction rate phenomenologically, the Eyring equation models individual elementary steps of a reaction. Thus, for a multistep process, there is no straightforward relationship between the two models. Nevertheless, the functional forms of the Arrhenius and Eyring equations are similar, and for a one-step process, simple and chemically meaningful correspondences can be drawn between Arrhenius and Eyring parameters.

Instead of also using E_a, the Eyring equation uses the concept of Gibbs energy and the symbol ΔG^‡ to denote the Gibbs energy of activation to achieve the transition state. In the equation, k_B and h are the Boltzmann and Planck constants, respectively. Although the equations look similar, it is important to note that the Gibbs energy contains an entropic term in addition to the enthalpic one. In the Arrhenius equation, this entropic term is accounted for by the pre-exponential factor A. More specifically, we can write the Gibbs free energy of activation in terms of enthalpy and entropy of activation: ΔG^‡ = ΔH^‡ – T ΔS^‡. Then, for a unimolecular, one-step reaction, the approximate relationships E_a = ΔH^‡ + RT and A = (k_BT/h) exp(1 + ΔS^‡/R) hold. Note, however, that in Arrhenius theory proper, A is temperature independent, while here, there is a linear dependence on T. For a one-step unimolecular process whose half-life at room temperature is about 2 hours, ΔG^‡ is approximately 23 kcal/mol. This is also the roughly the magnitude of E_a for a reaction that proceeds over several hours at room temperature. Due to the relatively small magnitude of TΔS^‡ and RT at ordinary temperatures for most reactions, in sloppy discourse, E_a, ΔG^‡, and ΔH^‡ are often conflated and all referred to as the "activation energy".

The enthalpy, entropy and Gibbs energy of activation are more correctly written as Δ^‡H^o, Δ^‡S^o and Δ^‡G^o respectively, where the o indicates a quantity evaluated between standard states.[13][14] However, some authors omit the o in order to simplify the notation.[15][16]

The total free energy change of a reaction is independent of the activation energy however. Physical and chemical reactions can be either exergonic or endergonic, but the activation energy is not related to the spontaneity of a reaction. The overall reaction energy change is not altered by the activation energy.

In some cases, rates of reaction decrease with increasing temperature. When following an approximately exponential relationship so the rate constant can still be fit to an Arrhenius expression, this results in a negative value of E_a. Elementary reactions exhibiting these negative activation energies are typically barrierless reactions, in which the reaction proceeding relies on the capture of the molecules in a potential well. Increasing the temperature leads to a reduced probability of the colliding molecules capturing one another (with more glancing collisions not leading to reaction as the higher momentum carries the colliding particles out of the potential well), expressed as a reaction cross section that decreases with increasing temperature. Such a situation no longer leads itself to direct interpretations as the height of a potential barrier.[17]

These are PES profiles for the reaction of hydrogen gas and tungsten. The reaction profile in the left shows a 2 dimensional pathway of the procedure. On the right side it is shown a 1 dimension perspective of the same trajectory.

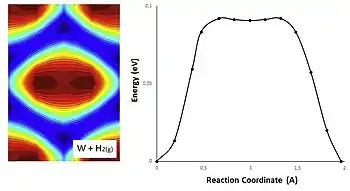
Activation energy can be represented in 2D Potential Energy Surfaces (PES), where the relation between the geometry of the reactants and the energy involved is represented as a topographic map.

In the following graphic there is a representation of a reaction between hydrogen in the gas phase and a metal: tungsten. The potential energy is obtained with PES calculations and consistent with the position of H from the NEB method calculations. A 2-dimensional interpolation with the spline method can be used to evaluate the potential energy at these positions.[18] Products and reactants can be found in the blue surface, however the red surface corresponds to the steady-state approximation.

The depics correspond to the trajectories. The bluer the surface, the stronger the hydrogen bonds, so blue colors represent minima energy and red colors are maxima. Tungsten’s PES is symmetric, and has a dip at the bridge site, this dip corresponds to the change of color in the center of the depic.

The bluer the surface between the energy minima, the lower the energy barriers, and therefore the more easily hydrogen travels along the surfaces.

• Activation energy asymptotics
• Chemical kinetics
• Fire point
• Mean kinetic temperature
• Quantum tunnelling
• Hydrogen safety
• Dust explosion
• Spark plug