Basic reproduction number
In epidemiology, the basic reproduction number, or basic reproductive number (sometimes called basic reproduction ratio or basic reproductive rate), denoted (pronounced R nought or R zero),[21] of an infection is the expected number of cases directly generated by one case in a population where all individuals are susceptible to infection.[17] The definition assumes that no other individuals are infected or immunized (naturally or through vaccination). Some definitions, such as that of the Australian Department of Health, add the absence of "any deliberate intervention in disease transmission".[22] The basic reproduction number is not the same as the effective reproduction number (usually written [t for time], sometimes ),[23] which is the number of cases generated in the current state of a population, which does not have to be the uninfected state. is a dimensionless number and not a rate, which would have units of time−1,[24] or units of time like doubling time.[25]
| Disease | Transmission | |
|---|---|---|
| Measles | Aerosol | 12–18[1] |
| Chickenpox (varicella) | Aerosol | 10–12[2] |
| Mumps | Respiratory droplets | 10–12[3] |
| Rubella | Respiratory droplets | 6–7[4] |
| Polio | Fecal–oral route | 5–7[5] |
| Pertussis | Respiratory droplets | 5.5[6] |
| Smallpox | Respiratory droplets | 3.5–6[7] |
| COVID-19 | Respiratory droplets and aerosol[8] | 3.3–5.7[9][10] |
| HIV/AIDS | Body fluids | 2–5[11] |
| Common cold | Respiratory droplets | 2–3[12] |
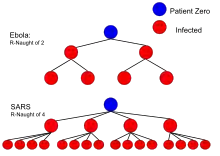
| SARS | Respiratory droplets | 0.19–1.1[13] |
| Diphtheria | Saliva | 1.7–4.3[14] |
| Influenza (1918 pandemic strain) | Respiratory droplets | 1.4–2.8[15] |
| Ebola (2014 Ebola outbreak) | Body fluids | 1.5–1.9[16] |
| Influenza (2009 pandemic strain) | Respiratory droplets | 1.2–1.6[17] |
| Influenza (seasonal strains) | Respiratory droplets | 0.9–2.1[18] |
| MERS | Respiratory droplets | 0.3–0.8[19] |
| Nipah virus | Body fluids | 0.48[20] |
is not a biological constant for a pathogen as it is also affected by other factors such as environmental conditions and the behaviour of the infected population. values are usually estimated from mathematical models, and the estimated values are dependent on the model used and values of other parameters. Thus values given in the literature only make sense in the given context and it is recommended not to use obsolete values or compare values based on different models.[26] does not by itself give an estimate of how fast an infection spreads in the population.
The most important uses of are determining if an emerging infectious disease can spread in a population and determining what proportion of the population should be immunized through vaccination to eradicate a disease. In commonly used infection models, when the infection will be able to start spreading in a population, but not if . Generally, the larger the value of , the harder it is to control the epidemic. For simple models, the proportion of the population that needs to be effectively immunized (meaning not susceptible to infection) to prevent sustained spread of the infection has to be larger than .[27] Conversely, the proportion of the population that remains susceptible to infection in the endemic equilibrium is .
The basic reproduction number is affected by several factors, including the duration of infectivity of affected people, the infectiousness of the microorganism, and the number of susceptible people in the population that the infected people contact.
History
The roots of the basic reproduction concept can be traced through the work of Ronald Ross, Alfred Lotka and others,[28] but its first modern application in epidemiology was by George MacDonald in 1952,[29] who constructed population models of the spread of malaria. In his work he called the quantity basic reproduction rate and denoted it by . Calling the quantity a rate can be misleading, insofar as "rate" can then be misinterpreted as a number per unit of time. "Number" or "ratio" is now preferred.
Definitions in specific cases
Contact rate and infectious period
Suppose that infectious individuals make an average of infection-producing contacts per unit time, with a mean infectious period of . Then the basic reproduction number is:
This simple formula suggests different ways of reducing and ultimately infection propagation. It is possible to decrease the number of infection-producing contacts per unit time by reducing the number of contacts per unit time (for example staying at home if the infection requires contact with others to propagate) or the proportion of contacts that produces infection (for example wearing some sort of protective equipment). Hence, it can also be written as[30]
where is the rate of contact between susceptible and infected individuals and is the transmissibility, i.e, the probability of infection given a contact. It is also possible to decrease the infectious period by finding and then isolating, treating or eliminating (as is often the case with animals) infectious individuals as soon as possible.
With varying latent periods
Latent period is the transition time between contagion event and disease manifestation. In cases of diseases with varying latent periods, the basic reproduction number can be calculated as the sum of the reproduction numbers for each transition time into the disease. An example of this is tuberculosis (TB). Blower and coauthors calculated from a simple model of TB the following reproduction number:[31]
In their model, it is assumed that the infected individuals can develop active TB by either direct progression (the disease develops immediately after infection) considered above as FAST tuberculosis or endogenous reactivation (the disease develops years after the infection) considered above as SLOW tuberculosis.[32]
Heterogeneous populations
In populations that are not homogeneous, the definition of is more subtle. The definition must account for the fact that a typical infected individual may not be an average individual. As an extreme example, consider a population in which a small portion of the individuals mix fully with one another while the remaining individuals are all isolated. A disease may be able to spread in the fully mixed portion even though a randomly selected individual would lead to fewer than one secondary case. This is because the typical infected individual is in the fully mixed portion and thus is able to successfully cause infections. In general, if the individuals infected early in an epidemic are on average either more likely or less likely to transmit the infection than individuals infected late in the epidemic, then the computation of must account for this difference. An appropriate definition for in this case is "the expected number of secondary cases produced, in a completely susceptible population, produced by a typical infected individual".[33]
The basic reproduction number can be computed as a ratio of known rates over time: if an infectious individual contacts β other people per unit time, if all of those people are assumed to contract the disease, and if the disease has a mean infectious period of 1/γ, then the basic reproduction number is just R0 = β/γ. Some diseases have multiple possible latency periods, in which case the reproduction number for the disease overall is the sum of the reproduction number for each transition time into the disease. For example, Blower et al.[34] model two forms of tuberculosis infection: in the fast case, the symptoms show up immediately after exposure; in the slow case, the symptoms develop years after the initial exposure (endogenous reactivation). The overall reproduction number is the sum of the two forms of contraction: R0 = R0FAST + R0SLOW.
Estimation methods
The basic reproduction number can be estimated through examining detailed transmission chains or through genomic sequencing. However, it is most frequently calculated using epidemiological models.[35] During an epidemic, typically the number of diagnosed infections over time is known. In the early stages of an epidemic, growth is exponential, with a logarithmic growth rate
For exponential growth, can be interpreted as the cumulative number of diagnoses (including individuals who have recovered) or the present number of infection cases; the logarithmic growth rate is the same for either definition. In order to estimate , assumptions are necessary about the time delay between infection and diagnosis and the time between infection and starting to be infectious.
In exponential growth, is related to the doubling time as
Simple model
If an individual, after getting infected, infects exactly new individuals only after exactly a time (the serial interval) has passed, then the number of infectious individuals over time grows as
or
The underlying matching differential equation is
or
In this case, or .
For example, with and , we would find .
If is time dependent
showing that it may be important to keep below 0, time-averaged, to avoid exponential growth.
Latent infectious period, isolation after diagnosis
In this model, an individual infection has the following stages:
- Exposed: an individual is infected, but has no symptoms and does not yet infect others. The average duration of the exposed state is .
- Latent infectious: an individual is infected, has no symptoms, but does infect others. The average duration of the latent infectious state is . The individual infects other individuals during this period.
- isolation after diagnosis: measures are taken to prevent further infections, for example by isolating the infected person.
This is a SEIR model and may be written in the following form[36]
This estimation method has been applied to COVID-19 and SARS. It follows from the differential equation for the number of exposed individuals and the number of latent infectious individuals ,
The largest eigenvalue of the matrix is the logarithmic growth rate , which can be solved for .
In the special case , this model results in , which is different from the simple model above (). For example, with the same values and , we would find , rather than the true value of . The difference is due to a subtle difference in the underlying growth model; the matrix equation above assumes that newly infected patients are currently already contributing to infections, while in fact infections only occur due to the number infected at ago. A more correct treatment would require the use of delay differential equations.[37]
Effective reproduction number
In reality, varying proportions of the population are immune to any given disease at any given time. To account for this, the effective reproduction number is used, usually written as , or the average number of new infections caused by a single infected individual at time t in the partially susceptible population. It can be found by multiplying by the fraction S of the population that is susceptible. When the fraction of the population that is immune increases (i. e. the susceptible population S decreases) so much that drops below 1, "herd immunity" has been achieved and the number of cases occurring in the population will gradually decrease to zero.[38][39][40]
Limitations of R0
Use of in the popular press has led to misunderstandings and distortions of its meaning. can be calculated from many different mathematical models. Each of these can give a different estimate of , which needs to be interpreted in the context of that model. Therefore, the contagiousness of different infectious agents cannot be compared without recalculating with invariant assumptions. values for past outbreaks might not be valid for current outbreaks of the same disease. Generally speaking, can be used as a threshold, even if calculated with different methods: if , the outbreak will die out, and if , the outbreak will expand. In some cases, for some models, values of can still lead to self-perpetuating outbreaks. This is particularly problematic if there are intermediate vectors between hosts, such as malaria.[41] Therefore, comparisons between values from the "Values of of well-known infectious diseases" table should be conducted with caution.
Although cannot be modified through vaccination or other changes in population susceptibility, it can vary based on a number of biological, sociobehavioral, and environmental factors.[26] It can also be modified by physical distancing and other public policy or social interventions,[42][26] although some historical definitions exclude any deliberate intervention in reducing disease transmission, including nonpharmacological interventions.[22] And indeed, whether nonpharmacological interventions are included in often depends on the paper, disease, and what if any intervention is being studied.[26] This creates some confusion, because is not a constant; whereas most mathematical parameters with "nought" subscripts are constants.
depends on many factors, many of which need to be estimated. Each of these factors adds to uncertainty in estimates of . Many of these factors are not important for informing public policy. Therefore, public policy may be better served by metrics similar to , but which are more straightforward to estimate, such as doubling time or half-life (t1⁄2).[43][44]
Methods used to calculate include the survival function, rearranging the largest eigenvalue of the Jacobian matrix, the next-generation method,[45] calculations from the intrinsic growth rate,[46] existence of the endemic equilibrium, the number of susceptibles at the endemic equilibrium, the average age of infection[47] and the final size equation. Few of these methods agree with one another, even when starting with the same system of differential equations.[41] Even fewer actually calculate the average number of secondary infections. Since is rarely observed in the field and is usually calculated via a mathematical model, this severely limits its usefulness.[48]
In popular culture
In the 2011 film Contagion, a fictional medical disaster thriller, a blogger's calculations for are presented to reflect the progression of a fatal viral infection from case studies to a pandemic. The methods depicted were faulty.[42]
See also
Notes
- Compartmental models in epidemiology describe disease dynamics over time in a population of susceptible (S), infectious (I), and recovered (R) people using the SIR model. Note that in the SIR model, and are different quantities – the former describes the number of recovered at t = 0 whereas the latter describes the ratio between the frequency of contacts to the frequency of recovery.
- According to Guangdong Provincial Center for Disease Control and Prevention, "The effective reproductive number (R or Re[49]) is more commonly used to describe transmissibility, which is defined as the average number of secondary cases generated by per [sic] infectious case." For example, by one preliminary estimate during the ongoing pandemic, the effective reproductive number for SARS-CoV-2 was found to be 2.9, whereas for SARS it was 1.77.
References
- Guerra, Fiona M.; Bolotin, Shelly; Lim, Gillian; Heffernan, Jane; Deeks, Shelley L.; Li, Ye; Crowcroft, Natasha S. (December 1, 2017). "The basic reproduction number (R0) of measles: a systematic review". The Lancet Infectious Diseases. 17 (12): e420–e428. doi:10.1016/S1473-3099(17)30307-9. ISSN 1473-3099. PMID 28757186. Retrieved March 18, 2020.
- Ireland's Health Services. Health Care Worker Information (PDF). Retrieved March 27, 2020.
- Australian government Department of Health Mumps Laboratory Case Definition (LCD)
- Centres for Disease Control and Prevention; World Health Organization (2001). "History and Epidemiology of Global Smallpox Eradication". A module of the training course "Smallpox: Disease, Prevention, and Intervention". Slide 17. This gives sources as "Modified from Epid Rev 1993;15: 265-302, Am J Prev Med 2001; 20 (4S): 88-153, MMWR 2000; 49 (SS-9); 27-38".
- Eisenberg, Joseph (February 12, 2020). "R0: How Scientists Quantify the Intensity of an Outbreak Like Coronavirus and Its Pandemic Potential". sph.umich.edu. Retrieved September 4, 2020.
- Kretzschmar M, Teunis PF, Pebody RG (2010). "Incidence and reproduction numbers of pertussis: estimates from serological and social contact data in five European countries". PLOS Med. 7 (6): e1000291. doi:10.1371/journal.pmed.1000291. PMC 2889930. PMID 20585374.
- Gani, Raymond; Leach, Steve (December 2001). "Transmission potential of smallpox in contemporary populations". Nature. 414 (6865): 748–751. doi:10.1038/414748a. ISSN 1476-4687. PMID 11742399. S2CID 52799168. Retrieved March 18, 2020.
- Prather KA, Marr LC, Schooley RT, et al. (October 16, 2020). "Airborne transmission of SARS-CoV-2" (PDF). Science. 370 (6514): 303–304. doi:10.1126/science.abf0521. Archived from the original on October 5, 2020. Retrieved October 30, 2020.
- Sanche, S.; Lin, Y. T.; Xu, C.; Romero-Severson, E.; Hengartner, E.; Ke, R. (July 2020). "High Contagiousness and Rapid Spread of Severe Acute Respiratory Syndrome Coronavirus 2". Emerging Infectious Diseases. 26 (7): 1470–1477. doi:10.3201/eid2607.200282. PMC 7323562. PMID 32255761.
- "Novel Corona virus - Information for Clinicians" (PDF). Australian Government - Department of Health. July 6, 2020.
- "Playing the Numbers Game: R0". National Emerging Special Pathogen Training and Education Center. Archived from the original on May 12, 202. Retrieved December 27, 2020.
[...] while infections that require sexual contact like HIV have a lower R0 (2-5).
- Freeman, Colin. "Magic formula that will determine whether Ebola is beaten". The Telegraph. Telegraph.Co.Uk. Retrieved March 30, 2020.
- Chowell G, Castillo-Chavez C, Fenimore PW, Kribs-Zaleta CM, Arriola L, Hyman JM (2004). "Model parameters and outbreak control for SARS". Emerg Infect Dis. 10 (7): 1258‐1263. doi:10.3201/eid1007.030647. PMC 3323341. PMID 15324546.
- Truelove, Shaun A.; Keegan, Lindsay T.; Moss, William J.; Chaisson, Lelia H.; Macher, Emilie; Azman, Andrew S.; Lessler, Justin (2019). "Clinical and Epidemiological Aspects of Diphtheria: A Systematic Review and Pooled Analysis". Clinical Infectious Diseases. 71 (1): 89–97. doi:10.1093/cid/ciz808. PMC 7312233. PMID 31425581.
- Ferguson NM; Cummings DA; Fraser C; Cajka JC; Cooley PC; Burke DS (2006). "Strategies for mitigating an influenza pandemic". Nature. 442 (7101): 448–452. Bibcode:2006Natur.442..448F. doi:10.1038/nature04795. PMC 7095311. PMID 16642006.
- Khan, Adnan; Naveed, Mahim; Dur-e-Ahmad, Muhammad; Imran, Mudassar (February 24, 2015). "Estimating the basic reproductive ratio for the Ebola outbreak in Liberia and Sierra Leone". Infectious Diseases of Poverty. 4: 13. doi:10.1186/s40249-015-0043-3. ISSN 2049-9957. PMC 4347917. PMID 25737782.
- Fraser, Christophe; Donnelly, Christl A.; Cauchemez, Simon; Hanage, William P.; Van Kerkhove, Maria D.; Hollingsworth, T. Déirdre; Griffin, Jamie; Baggaley, Rebecca F.; Jenkins, Helen E.; Lyons, Emily J.; Jombart, Thibaut (June 19, 2009). "Pandemic Potential of a Strain of Influenza A (H1N1): Early Findings". Science. 324 (5934): 1557–1561. Bibcode:2009Sci...324.1557F. doi:10.1126/science.1176062. ISSN 0036-8075. PMC 3735127. PMID 19433588.
- Coburn BJ; Wagner BG; Blower S (2009). "Modeling influenza epidemics and pandemics: insights into the future of swine flu (H1N1)". BMC Medicine. 7. Article 30. doi:10.1186/1741-7015-7-30. PMC 2715422. PMID 19545404.
- Kucharski, Adam; Althaus, Christian L. (2015). "The role of superspreading in Middle East respiratory syndrome coronavirus (MERS-CoV) transmission". Eurosurveillance. 20 (26): 14–8. doi:10.2807/1560-7917.ES2015.20.25.21167. PMID 26132768.
- https://edisciplinas.usp.br/pluginfile.php/4483966/mod_folder/content/0/NIPAH%20V%C3%8DRUS.pdf?forcedownload=1
- Milligan, Gregg N.; Barrett, Alan D. T. (2015). Vaccinology : an essential guide. Chichester, West Sussex: Wiley Blackwell. p. 310. ISBN 978-1-118-63652-7. OCLC 881386962.
- Becker, Niels G.; Glass, Kathryn; Barnes, Belinda; Caley, Peter; Philp, David; McCaw, James; McVernon, Jodie; Wood, James (April 2006). "The reproduction number". Using Mathematical Models to Assess Responses to an Outbreak of an Emerged Viral Respiratory Disease. National Centre for Epidemiology and Population Health. ISBN 1-74186-357-0. Retrieved February 1, 2020.
- Adam, David (2020). "A guide to R — the pandemic's misunderstood metric". Nature. 583: 346–348. doi:10.1038/d41586-020-02009-w.
- Jones, James. "Notes On R0" (PDF). Stanford University.
- Siegel, Ethan. "Why 'Exponential Growth' Is So Scary For The COVID-19 Coronavirus". Forbes. Retrieved March 19, 2020.
- Delamater, Paul L.; Street, Erica J.; Leslie, Timothy F.; Yang, Y. Tony; Jacobsen, Kathryn H. (January 2019). "Complexity of the Basic Reproduction Number (R 0 )". Emerging Infectious Diseases. 25 (1): 1–4. doi:10.3201/eid2501.171901. ISSN 1080-6040. PMC 6302597. PMID 30560777.
- Fine, Paul; Eames, Ken; Heymann, David L. (April 1, 2011). ""Herd Immunity": A Rough Guide". Clinical Infectious Diseases. 52 (7): 911–916. doi:10.1093/cid/cir007. ISSN 1058-4838. PMID 21427399.
- Smith, David L.; Battle, Katherine E.; Hay, Simon I.; Barker, Christopher M.; Scott, Thomas W.; McKenzie, F. Ellis (April 5, 2012). "Ross, Macdonald, and a Theory for the Dynamics and Control of Mosquito-Transmitted Pathogens". PLOS Pathogens. 8 (4): e1002588. doi:10.1371/journal.ppat.1002588. ISSN 1553-7366. PMC 3320609. PMID 22496640.
- Macdonald, G. (September 1952). "The analysis of equilibrium in malaria". Tropical Diseases Bulletin. 49 (9): 813–829. ISSN 0041-3240. PMID 12995455.
- J.H. Jones, Notes on R0. Stanford University (2007).
- Blower, S. M.; Mclean, A. R.; Porco, T. C.; Small, P. M.; Hopewell, P. C.; Sanchez, M. A. (1995). "The intrinsic transmission dynamics of tuberculosis epidemics". Nature Medicine. 1 (8): 815–821. doi:10.1038/nm0895-815. PMID 7585186. S2CID 19795498.
- Ma Y, Horsburgh CR, White LF, Jenkins HE (September 2018). "Quantifying TB transmission: a systematic review of reproduction number and serial interval estimates for tuberculosis". Epidemiol Infect. 146 (12): 1478–1494. doi:10.1017/S0950268818001760. PMC 6092233. PMID 29970199.
- O Diekmann; J.A.P. Heesterbeek; J.A.J. Metz (1990). "On the definition and the computation of the basic reproduction ratio in models for infectious diseases in heterogeneous populations". Journal of Mathematical Biology. 28 (4): 356–382. doi:10.1007/BF00178324. hdl:1874/8051. PMID 2117040. S2CID 22275430.
- Blower, S. M., Mclean, A. R., Porco, T. C., Small, P. M., Hopewell, P. C., Sanchez, M. A., et al. (1995). "The intrinsic transmission dynamics of tuberculosis epidemics." Nature Medicine, 1, 815–821.
- Wohl, Shirlee; Schaffner, Stephen F.; Sabeti, Pardis C. (2016). "Genomic Analysis of Viral Outbreaks". Annual Review of Virology. 3 (1): 173–195. doi:10.1146/annurev-virology-110615-035747. PMC 5210220. PMID 27501264.
- Lipsitch, Marc; Cohen, Ted; Cooper, Ben; Robins, James M.; Ma, Stefan; James, Lyn; Gopalakrishna, Gowri; Chew, Suok Kai; Tan, Chorh Chuan; Samore, Matthew H.; Fisman, David (June 20, 2003). "Transmission Dynamics and Control of Severe Acute Respiratory Syndrome". Science. 300 (5627): 1966–1970. Bibcode:2003Sci...300.1966L. doi:10.1126/science.1086616. ISSN 0036-8075. PMC 2760158. PMID 12766207.
- Rihan, Fathalla A.; Anwar, M. Naim (2012). "Qualitative Analysis of Delayed SIR Epidemic Model with a Saturated Incidence Rate". International Journal of Differential Equations. 2012: 1–13. doi:10.1155/2012/408637. ISSN 1687-9643.
- Garnett, G. P. (February 1, 2005). "Role of Herd Immunity in Determining the Effect of Vaccines against Sexually Transmitted Disease". The Journal of Infectious Diseases. 191 (Suppl 1): S97–106. doi:10.1086/425271. PMID 15627236.
- Rodpothong, P; Auewarakul, P (2012). "Viral evolution and transmission effectiveness". World Journal of Virology. 1 (5): 131–34. doi:10.5501/wjv.v1.i5.131. PMC 3782273. PMID 24175217.
- Dabbaghian, V.; Mago, V. K. (2013). Theories and Simulations of Complex Social Systems. Springer. pp. 134–35. ISBN 978-3642391491. Retrieved March 29, 2015.
- Li J, Blakeley D, Smith? RJ (2011). "The Failure of ". Computational and Mathematical Methods in Medicine. 2011 (527610): 1–17. doi:10.1155/2011/527610. PMC 3157160. PMID 21860658.
- Byrne, Michael (October 6, 2014), "The Misunderstood Number That Predicts Epidemics", vice.com, retrieved March 23, 2020
- Balkew, Teshome Mogessie (December 2010). The SIR Model When S(t) is a Multi-Exponential Function (Thesis). East Tennessee State University.
- Ireland, MW, ed. (1928). The Medical Department of the United States Army in the World War, vol. IX: Communicable and Other Diseases. Washington: U.S.: U.S. Government Printing Office. pp. 116–7.
- Diekmann O, Heesterbeek JA (2000). "The Basic Reproduction Ratio". Mathematical Epidemiology of Infectious Diseases : Model Building, Analysis and Interpretation. New York: Wiley. pp. 73–98. ISBN 0-471-49241-8.
- Chowell G, Hengartnerb NW, Castillo-Chaveza C, Fenimorea PW, Hyman JM (2004). "The basic reproductive number of Ebola and the effects of public health measures: the cases of Congo and Uganda". Journal of Theoretical Biology. 229 (1): 119–126. arXiv:q-bio/0503006. doi:10.1016/j.jtbi.2004.03.006. PMID 15178190. S2CID 7298792.
- Ajelli M; Iannelli M; Manfredi P & Ciofi degli Atti, ML (2008). "Basic mathematical models for the temporal dynamics of HAV in medium-endemicity Italian areas". Vaccine. 26 (13): 1697–1707. doi:10.1016/j.vaccine.2007.12.058. PMID 18314231.
- Heffernan JM, Smith RJ, Wahl LM (2005). "Perspectives on the Basic Reproductive Ratio". Journal of the Royal Society Interface. 2 (4): 281–93. doi:10.1098/rsif.2005.0042. PMC 1578275. PMID 16849186.
- Held, Leonhard; Hens, Niel; O'Neill, Philip D.; Wallinga, Jacco (November 7, 2019). Handbook of Infectious Disease Data Analysis. CRC Press. p. 347. ISBN 978-1-351-83932-7.
Further reading
- Heesterbeek, J.A.P. (2002). "A brief history of and a recipe for its calculation". Acta Biotheoretica. 50 (3): 189–204. doi:10.1023/A:1016599411804. PMID 12211331. S2CID 10178944.
- Heffernan, J.M.; Smith, R.J.; Wahl, L.M. (October 2005). "Perspectives on the basic reproductive ratio". Journal of the Royal Society Interface. 2 (4): 281–293. doi:10.1098/rsif.2005.0042. PMC 1578275. PMID 16849186.
- Jones, James Holland (May 1, 2007). "Notes on " (PDF). Retrieved November 6, 2018.
- Van Den Driessche, P.; Watmough, James (2008). "Further Notes on the Basic Reproduction Number". Mathematical Epidemiology. Lecture Notes in Mathematics. 1945. pp. 159–178. doi:10.1007/978-3-540-78911-6_6. ISBN 978-3-540-78910-9.
