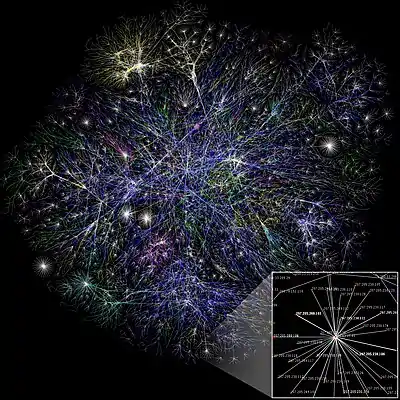
Complex network
In the context of network theory, a complex network is a graph (network) with non-trivial topological features—features that do not occur in simple networks such as lattices or random graphs but often occur in networks representing real systems. The study of complex networks is a young and active area of scientific research[1][2][3] (since 2000) inspired largely by empirical findings of real-world networks such as computer networks, biological networks, technological networks, brain networks, climate networks and social networks.
| Network science | ||||
|---|---|---|---|---|
| Network types | ||||
| Graphs | ||||
|
||||
| Models | ||||
|
||||
| ||||
|
||||
Definition
Most social, biological, and technological networks display substantial non-trivial topological features, with patterns of connection between their elements that are neither purely regular nor purely random. Such features include a heavy tail in the degree distribution, a high clustering coefficient, assortativity or disassortativity among vertices, community structure, and hierarchical structure. In the case of directed networks these features also include reciprocity, triad significance profile and other features. In contrast, many of the mathematical models of networks that have been studied in the past, such as lattices and random graphs, do not show these features. The most complex structures can be realized by networks with a medium number of interactions.[4] This corresponds to the fact that the maximum information content (entropy) is obtained for medium probabilities.
Two well-known and much studied classes of complex networks are scale-free networks[5] and small-world networks,[6][7] whose discovery and definition are canonical case-studies in the field. Both are characterized by specific structural features—power-law degree distributions for the former and short path lengths and high clustering for the latter. However, as the study of complex networks has continued to grow in importance and popularity, many other aspects of network structures have attracted attention as well.
Recently, the study of complex networks has been expanded to networks of networks.[8] If those networks are interdependent, they become significantly more vulnerable than single networks to random failures and targeted attacks and exhibit cascading failures and first-order percolation transitions.[9][10]
Furthermore, the collective behavior of a network in the presence of nodes failure and recovery has been studied.[11] It has been found that such a network can have spontaneous failures and spontaneous recoveries.
The field continues to develop at a brisk pace, and has brought together researchers from many areas including mathematics, physics, electric power systems,[12] biology,[13] climate,[14] computer science, sociology, epidemiology,[15] and others.[16] Ideas and tools from network science and engineering have been applied to the analysis of metabolic and genetic regulatory networks; the study of ecosystem stability and robustness;[17] clinical science;[18] the modeling and design of scalable communication networks such as the generation and visualization of complex wireless networks;[19] the development of vaccination strategies for the control of disease; [20][21] and a broad range of other practical issues. Research on networks are regularly published in the most visible scientific journals and obtain vigorous funding in many countries. Network theory has been found recently useful to identify bottlenecks in city traffic.[22] Network science is the topic of many conferences in a variety of different fields, and has been the subject of numerous books both for the lay person and for the expert.
Scale-free networks

A network is called scale-free[5][23] if its degree distribution, i.e., the probability that a node selected uniformly at random has a certain number of links (degree), follows a mathematical function called a power law. The power law implies that the degree distribution of these networks has no characteristic scale. In contrast, networks with a single well-defined scale are somewhat similar to a lattice in that every node has (roughly) the same degree. Examples of networks with a single scale include the Erdős–Rényi (ER) random graph, random regular graphs, regular lattices, and hypercubes. Some models of growing networks that produce scale-invariant degree distributions are the Barabási–Albert model and the fitness model. In a network with a scale-free degree distribution, some vertices have a degree that is orders of magnitude larger than the average - these vertices are often called "hubs", although this language is misleading as, by definition, there is no inherent threshold above which a node can be viewed as a hub. If there were such a threshold, the network would not be scale-free.
Interest in scale-free networks began in the late 1990s with the reporting of discoveries of power-law degree distributions in real world networks such as the World Wide Web, the network of Autonomous systems (ASs), some networks of Internet routers, protein interaction networks, email networks, etc. Most of these reported "power laws" fail when challenged with rigorous statistical testing, but the more general idea of heavy-tailed degree distributions -- which many of these networks do genuinely exhibit (before finite-size effects occur) -- are very different from what one would expect if edges existed independently and at random (i.e., if they followed a Poisson distribution). There are many different ways to build a network with a power-law degree distribution. The Yule process is a canonical generative process for power laws, and has been known since 1925. However, it is known by many other names due to its frequent reinvention, e.g., The Gibrat principle by Herbert A. Simon, the Matthew effect, cumulative advantage and, preferential attachment by Barabási and Albert for power-law degree distributions. Recently, Hyperbolic Geometric Graphs have been suggested as yet another way of constructing scale-free networks.
Some networks with a power-law degree distribution (and specific other types of structure) can be highly resistant to the random deletion of vertices—i.e., the vast majority of vertices remain connected together in a giant component.[24] Such networks can also be quite sensitive to targeted attacks aimed at fracturing the network quickly. When the graph is uniformly random except for the degree distribution, these critical vertices are the ones with the highest degree, and have thus been implicated in the spread of disease (natural and artificial) in social and communication networks, and in the spread of fads (both of which are modeled by a percolation or branching process). While random graphs (ER) have an average distance of order log N[6] between nodes, where N is the number of nodes, scale free graph can have a distance of log log N. Such graphs are called ultra small world networks.[25]
Small-world networks
A network is called a small-world network[6] by analogy with the small-world phenomenon (popularly known as six degrees of separation). The small world hypothesis, which was first described by the Hungarian writer Frigyes Karinthy in 1929, and tested experimentally by Stanley Milgram (1967), is the idea that two arbitrary people are connected by only six degrees of separation, i.e. the diameter of the corresponding graph of social connections is not much larger than six. In 1998, Duncan J. Watts and Steven Strogatz published the first small-world network model, which through a single parameter smoothly interpolates between a random graph and a lattice.[6] Their model demonstrated that with the addition of only a small number of long-range links, a regular graph, in which the diameter is proportional to the size of the network, can be transformed into a "small world" in which the average number of edges between any two vertices is very small (mathematically, it should grow as the logarithm of the size of the network), while the clustering coefficient stays large. It is known that a wide variety of abstract graphs exhibit the small-world property, e.g., random graphs and scale-free networks. Further, real world networks such as the World Wide Web and the metabolic network also exhibit this property.
In the scientific literature on networks, there is some ambiguity associated with the term "small world". In addition to referring to the size of the diameter of the network, it can also refer to the co-occurrence of a small diameter and a high clustering coefficient. The clustering coefficient is a metric that represents the density of triangles in the network. For instance, sparse random graphs have a vanishingly small clustering coefficient while real world networks often have a coefficient significantly larger. Scientists point to this difference as suggesting that edges are correlated in real world networks.
Spatial networks
Many real networks are embedded in space. Examples include, transportation and other infrastructure networks, brain neural networks. Several models for spatial networks have been developed.[26][27]
Spatial modular networks
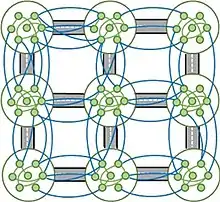
A model for spatially modular networks has been developed by Gross et al.[28] The model describes e.g., infrastructures in a country where communities (modules) represent cities with many connections located in two dimensional space. The links between communities (cities) are less and usually to nearest neighbors (see Fig. 2).
See also
Books
- B. S. Manoj, Abhishek Chakraborty, and Rahul Singh, Complex Networks: A Networking and Signal Processing Perspective, Pearson, New York, USA, February 2018. ISBN 978-0134786995
- S.N. Dorogovtsev and J.F.F. Mendes, Evolution of Networks: From biological networks to the Internet and WWW, Oxford University Press, 2003, ISBN 0-19-851590-1
- Duncan J. Watts, Six Degrees: The Science of a Connected Age, W. W. Norton & Company, 2003, ISBN 0-393-04142-5
- Duncan J. Watts, Small Worlds: The Dynamics of Networks between Order and Randomness, Princeton University Press, 2003, ISBN 0-691-11704-7
- Albert-László Barabási, Linked: How Everything is Connected to Everything Else, 2004, ISBN 0-452-28439-2
- Alain Barrat, Marc Barthelemy, Alessandro Vespignani, Dynamical processes on complex networks, Cambridge University Press, 2008, ISBN 978-0-521-87950-7
- Stefan Bornholdt (Editor) and Heinz Georg Schuster (Editor), Handbook of Graphs and Networks: From the Genome to the Internet, 2003, ISBN 3-527-40336-1
- Guido Caldarelli, Scale-Free Networks, Oxford University Press, 2007, ISBN 978-0-19-921151-7
- Guido Caldarelli, Michele Catanzaro, Networks: A Very Short Introduction Oxford University Press, 2012, ISBN 978-0-19-958807-7
- E. Estrada, "The Structure of Complex Networks: Theory and Applications", Oxford University Press, 2011, ISBN 978-0-199-59175-6
- Reuven Cohen and Shlomo Havlin, Complex Networks: Structure, Robustness and Function, Cambridge University Press, 2010, ISBN 978-0-521-84156-6
- Mark Newman, Networks: An Introduction, Oxford University Press, 2010, ISBN 978-0-19-920665-0
- Mark Newman, Albert-László Barabási, and Duncan J. Watts, The Structure and Dynamics of Networks, Princeton University Press, Princeton, 2006, ISBN 978-0-691-11357-9
- R. Pastor-Satorras and A. Vespignani, Evolution and Structure of the Internet: A statistical physics approach, Cambridge University Press, 2004, ISBN 0-521-82698-5
- T. Lewis, Network Science, Wiley 2009,
- Niloy Ganguly (Editor), Andreas Deutsch (Editor) and Animesh Mukherjee (Editor), Dynamics On and Of Complex Networks Applications to Biology, Computer Science, and the Social Sciences, 2009, ISBN 978-0-8176-4750-6
- Vito Latora, Vincenzo Nicosia, Giovanni Russo, Complex Networks: Principles, Methods and Applications, Cambridge University Press, 2017, ISBN 978-1107103184
References
- R. Albert and A.-L. Barabási (2002). "Statistical mechanics of complex networks". Reviews of Modern Physics. 74 (1): 47–49. arXiv:cond-mat/0106096. Bibcode:2002RvMP...74...47A. doi:10.1103/RevModPhys.74.47. S2CID 60545.
- Mark Newman (2010). "Networks: An Introduction". Oxford University Press. ISBN 978-0-19-920665-0.
- Reuven Cohen and Shlomo Havlin (2010). "Complex Networks: Structure, Robustness and Function". Cambridge University Press. ISBN 978-0-521-84156-6.
- T. Wilhelm, J. Kim (2008). "What is a complex graph?". Physica A. 387 (11): 2637–2652. Bibcode:2008PhyA..387.2637K. doi:10.1016/j.physa.2008.01.015.
- A. Barabasi, E. Bonabeau (2003). "Scale-Free Networks". Scientific American. 288 (5): 50–59. doi:10.1038/scientificamerican0503-60. PMID 12701331.
- S. H. Strogatz, D. J. Watts (1998). "Collective dynamics of 'small-world' networks". Nature. 393 (6684): 440–442. Bibcode:1998Natur.393..440W. doi:10.1038/30918. PMID 9623998. S2CID 4429113.
- H.E. Stanley, L.A.N. Amaral, A. Scala, M. Barthelemy (2000). "Classes of small-world networks". PNAS. 97 (21): 11149–52. arXiv:cond-mat/0001458. Bibcode:2000PNAS...9711149A. doi:10.1073/pnas.200327197. PMC 17168. PMID 11005838.
- Buldyrev, Sergey V.; Parshani, Roni; Paul, Gerald; Stanley, H. Eugene; Havlin, Shlomo (2010). "Catastrophic cascade of failures in interdependent networks". Nature. 464 (7291): 1025–1028. arXiv:0907.1182. Bibcode:2010Natur.464.1025B. doi:10.1038/nature08932. ISSN 0028-0836. PMID 20393559. S2CID 1836955.
- Parshani, Roni; Buldyrev, Sergey V.; Havlin, Shlomo (2010). "Interdependent Networks: Reducing the Coupling Strength Leads to a Change from a First to Second Order Percolation Transition". Physical Review Letters. 105 (4): 048701. arXiv:1004.3989. Bibcode:2010PhRvL.105d8701P. doi:10.1103/PhysRevLett.105.048701. ISSN 0031-9007. PMID 20867893. S2CID 17558390.
- J. Gao, S.V. Buldyrev, H.E. Stanley, S. Havlin (2012). "Networks formed from interdependent networks". Nature Physics. 8 (1): 40–48. Bibcode:2012NatPh...8...40G. doi:10.1038/nphys2180.CS1 maint: uses authors parameter (link)
- Majdandzic, Antonio; Podobnik, Boris; Buldyrev, Sergey V.; Kenett, Dror Y.; Havlin, Shlomo; Eugene Stanley, H. (2013). "Spontaneous recovery in dynamical networks". Nature Physics. 10 (1): 34–38. Bibcode:2014NatPh..10...34M. doi:10.1038/nphys2819. ISSN 1745-2473.
- Saleh, Mahmoud; Esa, Yusef; Mohamed, Ahmed (2018-05-29). "Applications of Complex Network Analysis in Electric Power Systems". Energies. 11 (6): 1381. doi:10.3390/en11061381.
- A. Bashan, R.P. Bartsch, J.W. Kantelhardt, S. Havlin, P.C. Ivanov (2012). "Network physiology reveals relations between network topology and physiological function". Nature Communications. 3: 72. arXiv:1203.0242. Bibcode:2012NatCo...3..702B. doi:10.1038/ncomms1705. PMC 3518900. PMID 22426223.CS1 maint: multiple names: authors list (link)
- J. Fan, J. Meng, X. Chen, Y. Ashkenazy, S. Havlin (2017). "Network approaches to climate science". Science China: Physics, Mechanics and Astronomy. 60 (1): 10531. Bibcode:2017SCPMA..60a0531F. doi:10.1007/s11433-016-0362-2.CS1 maint: multiple names: authors list (link)
- Lucas D Valdez, Lidia A Braunstein, Shlomo Havlin (2020). "Epidemic spreading on modular networks: The fear to declare a pandemic". Physical Review E. 101 (3): 032309. arXiv:1909.09695. Bibcode:2020PhRvE.101c2309V. doi:10.1103/PhysRevE.101.032309. PMID 32289896. S2CID 202719412.CS1 maint: multiple names: authors list (link)
- A.E. Motter, R. Albert (2012). "Networks in Motion". Physics Today. 65 (4): 43–48. arXiv:1206.2369. Bibcode:2012PhT....65d..43M. doi:10.1063/pt.3.1518. S2CID 12823922. Archived from the original on 2012-09-06.
- Johnson S, Domı́nguez-Garcı́a V, Donetti L, Muñoz MA (2014). "Trophic coherence determines food-web stability". Proc Natl Acad Sci USA. 111 (50): 17923–17928. arXiv:1404.7728. Bibcode:2014PNAS..11117923J. doi:10.1073/pnas.1409077111. PMC 4273378. PMID 25468963.CS1 maint: multiple names: authors list (link)
- S.G.Hofmann, J.E.Curtiss (2018). "A complex network approach to clinical science". European Journal of Clinical Investigation. 48 (8): e12986. doi:10.1111/eci.12986. PMID 29931701.
- Mouhamed Abdulla (2012-09-22). On the Fundamentals of Stochastic Spatial Modeling and Analysis of Wireless Networks and its Impact to Channel Losses. Ph.D. Dissertation, Dept. Of Electrical and Computer Engineering, Concordia Univ., Montréal, Québec, Canada, Sep. 2012. (phd). Concordia University. pp. (Ch.4 develops algorithms for complex network generation and visualization).
- R. Cohen, S. Havlin, D. Ben-Avraham (2003). "Efficient immunization strategies for computer networks and populations". Phys. Rev. Lett. 91 (24): 247901. arXiv:cond-mat/0207387. Bibcode:2003PhRvL..91x7901C. doi:10.1103/PhysRevLett.91.247901. PMID 14683159. S2CID 919625.CS1 maint: uses authors parameter (link)
- Chen, Y; Paul, G; Havlin, S; Liljeros, F; Stanley, H. E (2008). "Finding a Better Immunization Strategy". Phys. Rev. Lett. 101 (5): 058701. Bibcode:2008PhRvL.101e8701C. doi:10.1103/PhysRevLett.101.058701. PMID 18764435.
- Li, Daqing; Fu, Bowen; Wang, Yunpeng; Lu, Guangquan; Berezin, Yehiel; Stanley, H. Eugene; Havlin, Shlomo (2015). "Percolation transition in dynamical traffic network with evolving critical bottlenecks". Proceedings of the National Academy of Sciences. 112 (3): 669–672. Bibcode:2015PNAS..112..669L. doi:10.1073/pnas.1419185112. ISSN 0027-8424. PMC 4311803. PMID 25552558.
- R. Albert and A.-L. Barabási (2002). "Statistical mechanics of complex networks". Reviews of Modern Physics. 74 (1): 47–97. arXiv:cond-mat/0106096. Bibcode:2002RvMP...74...47A. doi:10.1103/RevModPhys.74.47. ISBN 978-3-540-40372-2. S2CID 60545.
- Cohen, Reuven; Erez, Keren; ben-Avraham, Daniel; Havlin, Shlomo (2000). "Resilience of the Internet to Random Breakdowns". Physical Review Letters. 85 (21): 4626–4628. arXiv:cond-mat/0007048. Bibcode:2000PhRvL..85.4626C. doi:10.1103/PhysRevLett.85.4626. ISSN 0031-9007. PMID 11082612. S2CID 15372152.
- R. Cohen, S. Havlin (2003). "Scale-free networks are ultrasmall". Phys. Rev. Lett. 90 (5): 058701. arXiv:cond-mat/0205476. Bibcode:2003PhRvL..90e8701C. doi:10.1103/physrevlett.90.058701. PMID 12633404. S2CID 10508339.
- Waxman B. M. (1988). "Routing of multipoint connections". IEEE J. Sel. Areas Commun. 6 (9): 1617–1622. doi:10.1109/49.12889.CS1 maint: uses authors parameter (link)
- Danziger, Michael M.; Shekhtman, Louis M.; Berezin, Yehiel; Havlin, Shlomo (2016). "The effect of spatiality on multiplex networks". EPL. 115 (3): 36002. arXiv:1505.01688. Bibcode:2016EL....11536002D. doi:10.1209/0295-5075/115/36002.CS1 maint: uses authors parameter (link)
- Bnaya Gross, Dana Vaknin, Sergey Buldyrev, Shlomo Havlin (2020). "Two transitions in spatial modular networks". New Journal of Physics. 22 (5): 053002. arXiv:2001.11435. Bibcode:2020NJPh...22e3002G. doi:10.1088/1367-2630/ab8263. S2CID 210966323.CS1 maint: multiple names: authors list (link)
- D. J. Watts and S. H. Strogatz (1998). "Collective dynamics of 'small-world' networks". Nature. 393 (6684): 440–442. Bibcode:1998Natur.393..440W. doi:10.1038/30918. PMID 9623998. S2CID 4429113.
- S. H. Strogatz (2001). "Exploring Complex Networks". Nature. 410 (6825): 268–276. Bibcode:2001Natur.410..268S. doi:10.1038/35065725. PMID 11258382.
- R. Albert and A.-L. Barabási (2002). "Statistical mechanics of complex networks". Reviews of Modern Physics. 74 (1): 47–97. arXiv:cond-mat/0106096. Bibcode:2002RvMP...74...47A. doi:10.1103/RevModPhys.74.47. S2CID 60545.
- S. N. Dorogovtsev and J.F.F. Mendes (2002). "Evolution of Networks". Adv. Phys. 51 (4): 1079–1187. arXiv:cond-mat/0106144. Bibcode:2002AdPhy..51.1079D. doi:10.1080/00018730110112519. S2CID 429546.
- M. E. J. Newman, The structure and function of complex networks, SIAM Review 45, 167-256 (2003)
- S. N. Dorogovtsev, A. V. Goltsev, and J. F. F. Mendes, Critical phenomena in complex networks, Rev. Mod. Phys. 80, 1275, (2008)
- G. Caldarelli, R. Marchetti, L. Pietronero, The Fractals Properties of Internet, Europhysics Letters 52, 386 (2000). https://arxiv.org/abs/cond-mat/0009178. DOI: 10.1209/epl/i2000-00450-8
- R. Cohen, K. Erez, D. ben-Avraham, S. Havlin, "Resilience of the Internet to random breakdown" Phys. Rev. Lett. 85, 4626 (2000). https://arxiv.org/abs/1004.3989
- R. Cohen, K. Erez, D. ben-Avraham, S. Havlin, "Breakdown of the Internet under intentional attack" Phys. Rev. Lett. 86, 3682 (2001)
- R. Cohen, S. Havlin, "Scale-free networks are ultrasmall" Phys. Rev. Lett. 90, 058701 (2003)
- A. E. Motter (2004). "Cascade control and defense in complex networks". Phys. Rev. Lett. 93 (9): 098701. arXiv:cond-mat/0401074. Bibcode:2004PhRvL..93i8701M. doi:10.1103/PhysRevLett.93.098701. PMID 15447153. S2CID 4856492.
- J. Lehnert, Controlling Synchronization Patterns in Complex Networks, springer 2016
- Dolev, Shlomi; Elovici, Yuval; Puzis, Rami (2010), "Routing betweenness centrality", J. ACM, 57 (4): 25:1–25:27, doi:10.1145/1734213.1734219, S2CID 15662473