Davydov soliton
Davydov soliton is a quantum quasiparticle representing an excitation propagating along the protein α-helix self-trapped amide I. It is a solution of the Davydov Hamiltonian. It is named for the Soviet and Ukrainian physicist Alexander Davydov. The Davydov model describes the interaction of the amide I vibrations with the hydrogen bonds that stabilize the α-helix of proteins. The elementary excitations within the α-helix are given by the phonons which correspond to the deformational oscillations of the lattice, and the excitons which describe the internal amide I excitations of the peptide groups. Referring to the atomic structure of an α-helix region of protein the mechanism that creates the Davydov soliton (polaron, exciton) can be described as follows: vibrational energy of the C=O stretching (or amide I) oscillators that is localized on the α-helix acts through a phonon coupling effect to distort the structure of the α-helix, while the helical distortion reacts again through phonon coupling to trap the amide I oscillation energy and prevent its dispersion. This effect is called self-localization or self-trapping.[3][4][5] Solitons in which the energy is distributed in a fashion preserving the helical symmetry are dynamically unstable, and such symmetrical solitons once formed decay rapidly when they propagate. On the other hand, an asymmetric soliton which spontaneously breaks the local translational and helical symmetries possesses the lowest energy and is a robust localized entity.[6]
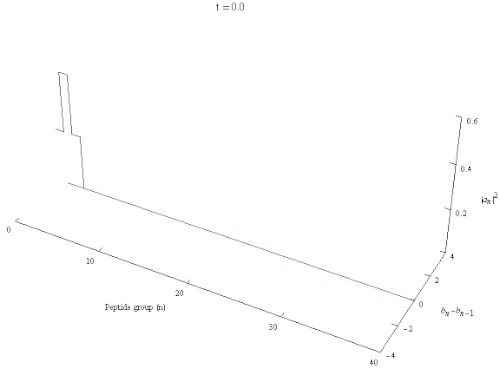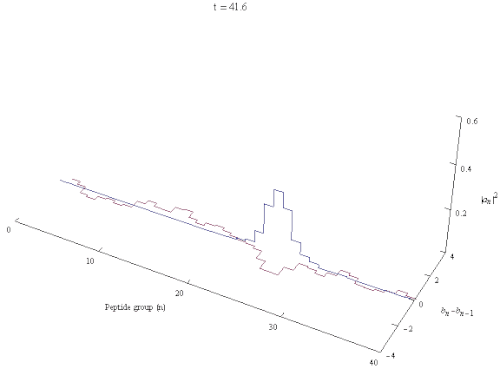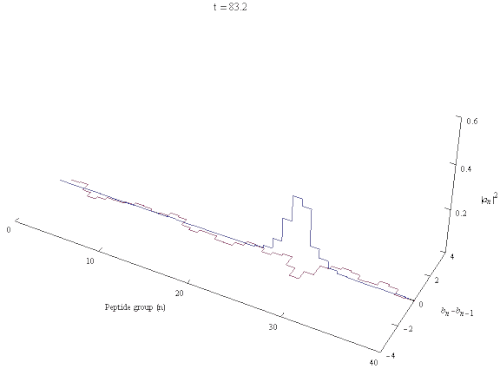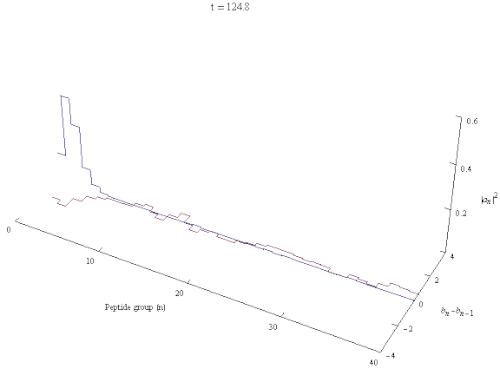
Davydov Hamiltonian
Davydov Hamiltonian is formally similar to the Fröhlich-Holstein Hamiltonian for the interaction of electrons with a polarizable lattice. Thus the Hamiltonian of the energy operator is
where is the quasiparticle (exciton) Hamiltonian, which describes the motion of the amide I excitations between adjacent sites; is the phonon Hamiltonian, which describes the vibrations of the lattice; and is the interaction Hamiltonian, which describes the interaction of the amide I excitation with the lattice.[3][4][5]
The quasiparticle (exciton) Hamiltonian is:
where the index counts the peptide groups along the α-helix spine, the index counts each α-helix spine, zJ is the energy of the amide I vibration (CO stretching), zJ is the dipole-dipole coupling energy between a particular amide I bond and those ahead and behind along the same spine, zJ is the dipole-dipole coupling energy between a particular amide I bond and those on adjacent spines in the same unit cell of the protein α-helix, and are respectively the boson creation and annihilation operator for a quasiparticle at the peptide group .[7][8][9]
The phonon Hamiltonian is
where is the displacement operator from the equilibrium position of the peptide group , is the momentum operator of the peptide group , is the mass of the peptide group , and N/m is an effective elasticity coefficient of the lattice (the spring constant of a hydrogen bond).[8]
Finally, the interaction Hamiltonian is
where pN is an anharmonic parameter arising from the coupling between the quasiparticle (exciton) and the lattice displacements (phonon) and parameterizes the strength of the exciton-phonon interaction.[8] The value of this parameter for α-helix has been determined via comparison of the theoretically calculated absorption line shapes with the experimentally measured ones.
Davydov soliton properties
There are three possible fundamental approaches for deriving equations of motion from Davydov Hamiltonian:
- quantum approach, in which both the amide I vibration (excitons) and the lattice site motion (phonons) are treated quantum mechanically;[10]
- mixed quantum-classical approach, in which the amide I vibration is treated quantum mechanically but the lattice is classical;[9]
- classical approach, in which both the amide I and the lattice motions are treated classically.[11]
The mathematical techniques that are used to analyze the Davydov soliton are similar to some that have been developed in polaron theory.[12] In this context, the Davydov soliton corresponds to a polaron that is:
- large so the continuum limit approximation is justified,[8]
- acoustic because the self-localization arises from interactions with acoustic modes of the lattice,[8]
- weakly coupled because the anharmonic energy is small compared with the phonon bandwidth.[8]
The Davydov soliton is a quantum quasiparticle and it obeys Heisenberg's uncertainty principle. Thus any model that does not impose translational invariance is flawed by construction.[8] Supposing that the Davydov soliton is localized to 5 turns of the α-helix results in significant uncertainty in the velocity of the soliton m/s, a fact that is obscured if one models the Davydov soliton as a classical object.
References
- Georgiev, Danko D.; Glazebrook, James F. (2019). "On the quantum dynamics of Davydov solitons in protein α-helices". Physica A: Statistical Mechanics and Its Applications. 517: 257–269. arXiv:1811.05886. doi:10.1016/j.physa.2018.11.026. MR 3880179.
- Georgiev, Danko D.; Glazebrook, James F. (2019). "Quantum tunneling of Davydov solitons through massive barriers". Chaos, Solitons and Fractals. 123: 275–293. arXiv:1904.09822. doi:10.1016/j.chaos.2019.04.013. MR 3941070.
- Davydov, Alexander S. (1973). "The theory of contraction of proteins under their excitation". Journal of Theoretical Biology. 38 (3): 559–569. doi:10.1016/0022-5193(73)90256-7. PMID 4266326.
- Davydov, Alexander S. (1977). "Solitons and energy transfer along protein molecules". Journal of Theoretical Biology. 66 (2): 379–387. doi:10.1016/0022-5193(77)90178-3. PMID 886872.
- Davydov, Alexander S. (1979). "Solitons, bioenergetics, and the mechanism of muscle contraction". International Journal of Quantum Chemistry. 16 (1): 5–17. doi:10.1002/qua.560160104.
- Brizhik, Larissa; Eremko, Alexander; Piette, Bernard; Zakrzewski, Wojtek (2004). "Solitons in α-helical proteins". Physical Review E. 70 (3 Pt 1): 031914. arXiv:cond-mat/0402644. Bibcode:2004PhRvE..70a1914K. doi:10.1103/PhysRevE.70.011914. PMID 15524556.
- Hyman, James M.; McLaughlin, David W.; Scott, Alwyn C. (1981). "On Davydov's alpha-helix solitons". Physica D: Nonlinear Phenomena. 3 (1): 23–44. Bibcode:1981PhyD....3...23H. doi:10.1016/0167-2789(81)90117-2.
- Scott, Alwyn C. (1992). "Davydov's soliton". Physics Reports. 217 (1): 1–67. Bibcode:1992PhR...217....1S. doi:10.1016/0370-1573(92)90093-F.
- Cruzeiro-Hansson, Leonor; Takeno, Shozo (1997). "Davydov model: the quantum, mixed quantum-classical, and full classical systems". Physical Review E. 56 (1): 894–906. Bibcode:1997PhRvE..56..894C. doi:10.1103/PhysRevE.56.894.
- Kerr, William C.; Lomdahl, Peter S. (1987). "Quantum-mechanical derivation of the equations of motion for Davydov solitons". Physical Review B. 35 (7): 3629–3632. doi:10.1103/PhysRevB.35.3629. hdl:10339/15922. PMID 9941870.
- Škrinjar, M. J.; Kapor, D. V.; Stojanović, S. D. (1988). "Classical and quantum approach to Davydov's soliton theory". Physical Review A. 38 (12): 6402–6408. doi:10.1103/PhysRevA.38.6402. PMID 9900400.
- Sun, Jin; Luo, Bin; Zhao, Yang (2010). "Dynamics of a one-dimensional Holstein polaron with the Davydov ansätze". Physical Review B. 82 (1): 014305. arXiv:1001.3198. doi:10.1103/PhysRevB.82.014305.
