Icositrigon

A regular icositrigon is represented by Schläfli symbol {23}.

A regular icositrigon has internal angles of ${\displaystyle {\frac {3780}{23}}}$ degrees, with an area of ${\displaystyle A={\frac {23}{4}}a^{2}\cot {\frac {\pi }{23}}=23r^{2}\tan {\frac {\pi }{23}}\simeq 41.8344\,a^{2},}$ where ${\displaystyle a}$ is side length and ${\displaystyle r}$ is the inradius, or apothem.

In addition to not being constructible with a compass and straightedge or angle trisection,[1] on account of the number 23 being neither a Fermat nor Pierpont prime, the regular icositrigon is the smallest regular polygon that is not constructible even with neusis, after the discovery of neusis construction of the hendecagon by Elliot Benjamin and Chip Snyder in 2014.[2]

Concerning the nonconstructability of the regular icositrigon, A. Baragar (2002) showed it is not possible to construct a regular 23-gon using only a compass and twice-notched straightedge by demonstrating that every point constructible with said method lies in a tower of fields over ${\displaystyle \mathbb {Q} }$ such that ${\displaystyle \mathbb {Q} =K_{0}\subset K_{1}\subset \dots \subset K_{n}=K}$, being a sequence of nested fields in which the degree of the extension at each step is 2, 3, 5, or 6.

Suppose ${\displaystyle \alpha }$ in ${\displaystyle \mathbb {C} }$ is constructible using a compass and twice-notched straightedge. Then ${\displaystyle \alpha }$ belongs to a field ${\displaystyle K}$ that lies in a tower of fields ${\displaystyle \mathbb {Q} =K_{0}\subset K_{1}\subset \dots \subset K_{n}=K}$ for which the index [${\displaystyle K_{j}}$ : K_j−1] at each step is 2, 3, 5, or 6. In particular, if ${\displaystyle N=}$[${\displaystyle K}$: ${\displaystyle \mathbb {Q} }$], then the only primes dividing ${\displaystyle N}$ are 2, 3, and 5. (Theorem 5.1)

If we can construct the regular p-gon, then we can construct ${\displaystyle \zeta _{p}=e^{\frac {2\pi i}{p}}}$, which is the root of an irreducible polynomial of degree ${\displaystyle p}$ − ${\displaystyle 1}$. By Theorem 5.1, ${\displaystyle \zeta _{p}}$ lies in a field ${\displaystyle K}$ of degree ${\displaystyle N}$ over ${\displaystyle \mathbb {Q} }$, where the only primes that divide ${\displaystyle N}$ are 2, 3, and 5. But ${\displaystyle \mathbb {Q} }$[${\displaystyle \zeta _{p}}$] is a subfield of ${\displaystyle K}$, so ${\displaystyle p}$ − ${\displaystyle 1}$ divides ${\displaystyle N}$. In particular, for ${\displaystyle p=23}$, ${\displaystyle N}$ must be divisible by 11, and for ${\displaystyle p=29}$, N must be divisible by 7.[3]

It should also be noted that an icositrigon is not origami constructible either, given 23 is not a Pierpont prime, nor a power of two or three.[4] However, it can be made constructible via the use of the Quadratrix of Hippias, Archimedean spiral, and other auxiliary curves; yet this is true for all regular polygons.[5]

Below is a table of five regular icositrigrams, or star 23-gons, labeled with their respective Schläfli symbol {23/q}, 2 ${\displaystyle \leq }$ q ${\displaystyle \leq }$ 11 where q is prime.

{23/2}

{23/3}

{23/5}

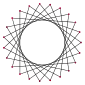{23/7}

{23/11}

• Detection of Interesting Properties in Regular Polygons