Polytope families
There are several families of symmetric polytopes with irreducible symmetry which have a member in more than one dimensionality. These are tabulated here with Petrie polygon projection graphs and Coxeter-Dynkin diagrams.
| Table of irreducible polytope families | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family n |
n-simplex | n-hypercube | n-orthoplex | n-demicube | 1k2 | 2k1 | k21 | pentagonal polytope | ||||||||
| Group | An | Bn |
|
|
Hn | |||||||||||
| 2 |  |
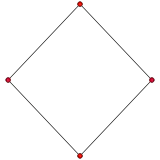 |
 p-gon (example: p=7) |
 Hexagon |
 Pentagon | |||||||||||
| 3 | 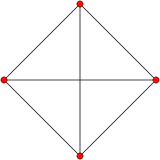 Tetrahedron |
 Cube |
 Octahedron |
 Tetrahedron |
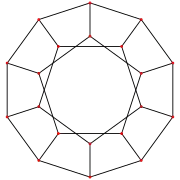 Dodecahedron |
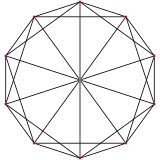 Icosahedron | ||||||||||
| 4 |  5-cell |
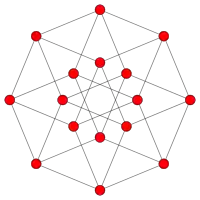 |
 16-cell |
 |
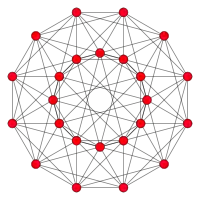 24-cell |
 120-cell |
 600-cell | |||||||||
| 5 |  5-simplex |
 5-cube |
 5-orthoplex |
 5-demicube |
||||||||||||
| 6 |  6-simplex |
 6-cube |
 6-orthoplex |
 6-demicube |
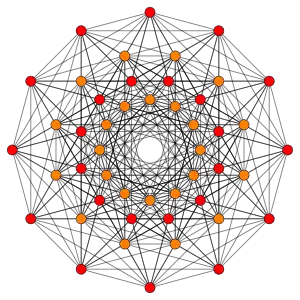 122 |
 221 |
||||||||||
| 7 | 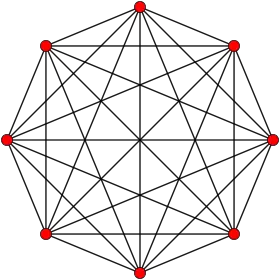 7-simplex |
 7-cube |
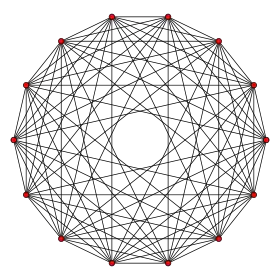 7-orthoplex |
 7-demicube |
 132 |
 231 |
 321 |
|||||||||
| 8 | 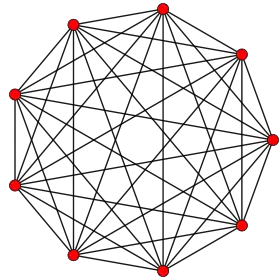 8-simplex |
 8-cube |
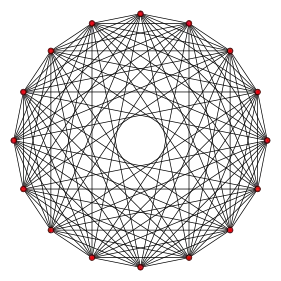 8-orthoplex |
 8-demicube |
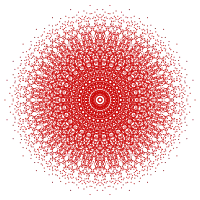 142 |
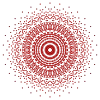 241 |
 421 |
|||||||||
| 9 | 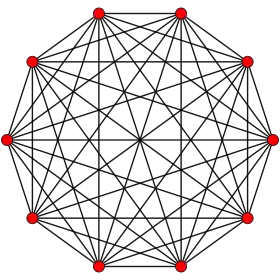 9-simplex |
 9-cube |
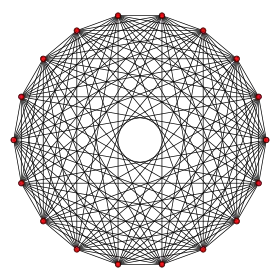 9-orthoplex |
 9-demicube |
||||||||||||
| 10 |  10-simplex |
 10-cube |
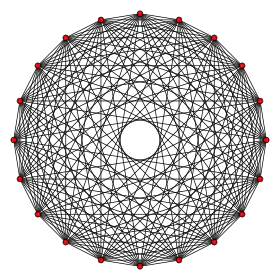 10-orthoplex |
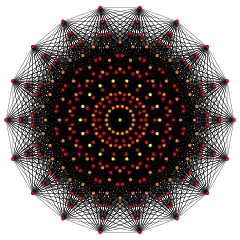 10-demicube |
||||||||||||
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.