Uniform 1 k2 polytope

In geometry, 1k2 polytope is a uniform polytope in n-dimensions (n = k+4) constructed from the En Coxeter group. The family was named by their Coxeter symbol 1k2 by its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of the 1-node sequence. It can be named by an extended Schläfli symbol {3,3k,2}.

Family members

The family starts uniquely as 6-polytopes, but can be extended backwards to include the 5-demicube (demipenteract) in 5-dimensions, and the 4-simplex (5-cell) in 4-dimensions.

Each polytope is constructed from 1k-1,2 and (n-1)-demicube facets. Each has a vertex figure of a {31,n-2,2} polytope is a birectified n-simplex, t2{3n}.

The sequence ends with k=6 (n=10), as an infinite tessellation of 9-dimensional hyperbolic space.

The complete family of 1k2 polytope polytopes are:

  1. 5-cell: 102, (5 tetrahedral cells)
  2. 112 polytope, (16 5-cell, and 10 16-cell facets)
  3. 122 polytope, (54 demipenteract facets)
  4. 132 polytope, (56 122 and 126 demihexeract facets)
  5. 142 polytope, (240 132 and 2160 demihepteract facets)
  6. 152 honeycomb, tessellates Euclidean 8-space (∞ 142 and ∞ demiocteract facets)
  7. 162 honeycomb, tessellates hyperbolic 9-space (∞ 152 and ∞ demienneract facets)

Elements
Gosset 1k2 figures
n 1k2 Petrie
polygon
projection		 Name
Coxeter-Dynkin
diagram		 Facets Elements
1k-1,2 (n-1)-demicube Vertices Edges Faces Cells 4-faces 5-faces 6-faces 7-faces
4 102 120
 -- 5
110
 5 10 10
 5
        
5 112 121
 16
120
 10
111
 16 80 160
 120
 26
      
6 122 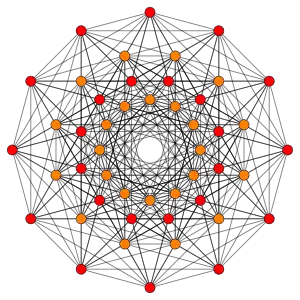122
 27
112
 27
121
 72 720 2160
 2160
 702
 54
    
7 132 132
 56
122
 126
131
 576 10080 40320
 50400
 23688
 4284
 182
  
8 142 142
 240
132
 2160
141
 17280 483840 2419200
 3628800
 2298240
 725760
 106080
 2400
9 152 152

(8-space tessellation)		 ∞
142
 ∞
151
 ∞
10 162 162

(9-space hyperbolic tessellation)		 ∞
152		 ∞
161
 ∞

See also

References
  • Alicia Boole Stott Geometrical deduction of semiregular from regular polytopes and space fillings, Verhandelingen of the Koninklijke academy van Wetenschappen width unit Amsterdam, Eerste Sectie 11,1, Amsterdam, 1910
    • Stott, A. B. "Geometrical Deduction of Semiregular from Regular Polytopes and Space Fillings." Verhandelingen der Koninklijke Akad. Wetenschappen Amsterdam 11, 3-24, 1910.
    • Alicia Boole Stott, "Geometrical deduction of semiregular from regular polytopes and space fillings," Verhandelingen der Koninklijke Akademie van Wetenschappen te Amsterdam, (eerste sectie), Vol. 11, No. 1, pp. 1–24 plus 3 plates, 1910.
    • Stott, A. B. 1910. "Geometrical Deduction of Semiregular from Regular Polytopes and Space Fillings." Verhandelingen der Koninklijke Akad. Wetenschappen Amsterdam
  • Schoute, P. H., Analytical treatment of the polytopes regularly derived from the regular polytopes, Ver. der Koninklijke Akad. van Wetenschappen te Amsterdam (eerstie sectie), vol 11.5, 1913.
  • H. S. M. Coxeter: Regular and Semi-Regular Polytopes, Part I, Mathematische Zeitschrift, Springer, Berlin, 1940
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
  • H.S.M. Coxeter: Regular and Semi-Regular Polytopes, Part II, Mathematische Zeitschrift, Springer, Berlin, 1985
  • H.S.M. Coxeter: Regular and Semi-Regular Polytopes, Part III, Mathematische Zeitschrift, Springer, Berlin, 1988
Fundamental convex regular and uniform polytopes in dimensions 2–10
Family An Bn I2(p) / Dn E6 / E7 / E8 / F4 / G2 Hn
Regular polygon Triangle Square p-gon Hexagon Pentagon
Uniform polyhedron Tetrahedron Octahedron • Cube Demicube Dodecahedron • Icosahedron
Uniform 4-polytope 5-cell 16-cell • Tesseract Demitesseract 24-cell 120-cell • 600-cell
Uniform 5-polytope 5-simplex 5-orthoplex • 5-cube 5-demicube
Uniform 6-polytope 6-simplex 6-orthoplex • 6-cube 6-demicube 122 • 221
Uniform 7-polytope 7-simplex 7-orthoplex • 7-cube 7-demicube 132 • 231 • 321
Uniform 8-polytope 8-simplex 8-orthoplex • 8-cube 8-demicube 142 • 241 • 421
Uniform 9-polytope 9-simplex 9-orthoplex • 9-cube 9-demicube
Uniform 10-polytope 10-simplex 10-orthoplex • 10-cube 10-demicube
Uniform n-polytope n-simplex n-orthoplex • n-cube n-demicube 1k2 • 2k1 • k21 n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds
Fundamental convex regular and uniform honeycombs in dimensions 2-9
Space Family / /
E2 Uniform tiling {3[3]} δ3 hδ3 qδ3 Hexagonal
E3 Uniform convex honeycomb {3[4]} δ4 hδ4 qδ4
E4 Uniform 4-honeycomb {3[5]} δ5 hδ5 qδ5 24-cell honeycomb
E5 Uniform 5-honeycomb {3[6]} δ6 hδ6 qδ6
E6 Uniform 6-honeycomb {3[7]} δ7 hδ7 qδ7 222
E7 Uniform 7-honeycomb {3[8]} δ8 hδ8 qδ8 133 • 331
E8 Uniform 8-honeycomb {3[9]} δ9 hδ9 qδ9 152 • 251 • 521
E9 Uniform 9-honeycomb {3[10]} δ10 hδ10 qδ10
En-1 Uniform (n-1)-honeycomb {3[n]} δn hδn qδn 1k2 • 2k1 • k21
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.