Triaugmented triangular prism
In geometry, the triaugmented triangular prism, tetracaidecadeltahedron, or tetrakis triangular prism is one of the Johnson solids (J51). Each of its 14 faces is an equilateral triangle, making it a deltahedron. As the name suggests, it can be constructed by attaching equilateral square pyramids (J1) to each of the three equatorial faces of the triangular prism.
| Triaugmented triangular prism | |
|---|---|
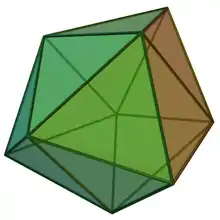 | |
| Type | Johnson J50 - J51 - J52 |
| Faces | 14 (2+2×6) triangles |
| Edges | 21 |
| Vertices | 9 |
| Vertex configuration | 3(34) 6(35) |
| Symmetry group | D3h |
| Dual polyhedron | Order-4 truncated triangular bipyramid (associahedron K5) |
| Properties | convex, deltahedron |
| Net | |
 | |
A Johnson solid is one of 92 strictly convex polyhedra that is composed of regular polygon faces but are not uniform polyhedra (that is, they are not Platonic solids, Archimedean solids, prisms, or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.[1]
Dual polyhedron

The dual of the triaugmented triangular prism is an order-4 truncated triangular bipyramid, also known as an order-5 associahedron. This transparent image shows its three square, and six congruent irregular pentagonal faces. Edges are colored to distinguish the 3 different edge lengths.
External links
- Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603.
