Armadillo projection

The armadillo projection is a map projection used for world maps. It is neither conformal nor equal-area but instead affords a view evoking a perspective projection while showing most of the globe instead of the half or less that a perspective would. The projection was presented in 1943 by Erwin Raisz (1893–1968) as part of a series of "orthoapsidal" projections, which are perspectives of the globe projected onto various surfaces. This one in the series has the globe projected onto half a torus. Raisz singled it out and named it the "armadillo" projection.[1]

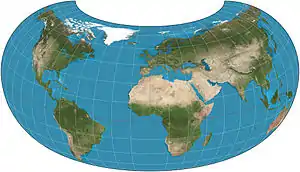
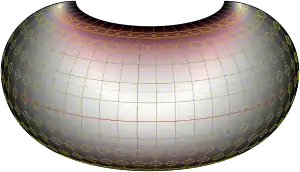
Raisz armadillo projection of the world.
Tissot indicatrix on Raisz armadillo projection, 15° graticule. Color shows angular deformation and areal inflation/deflation in a bivariate scheme: The lighter the color, the less distortion. The redder, the more angular distortion. The greener, the more areal inflation or deflation.

The toroidal shape and the angle it is viewed from tend to emphasize continental areas by eliminating or foreshortening swaths of ocean. In the pure case of projecting the half-torus, New Zealand cannot be seen, as in the images here. However, in publications, the projection often develops a "pigtail" which shows the rest of Australia as well as New Zealand.

Raisz coined the term orthoapsidal as a combination of orthographic and apsidal. He used it to mean drawing a parallel-meridian network, or graticule, on any suitable solid other than a sphere, and then making an orthographic projection of that.[2]

Formulas

Given a radius of sphere R, central meridian λ0 and a point with geographical latitude φ and longitude λ, plane coordinates x and y can be computed using the following formulas:[3]

In this formulation, no latitude more southerly than φs should be plotted for the given longitude. The y-axis coincides with the central meridian.

See also

References
  1. Snyder, John P. (1993). Flattening the Earth: 2000 Years of Map Projections. Chicago: University of Chicago Press. pp. 267–268.
  2. Raisz, Erwin J. (1962). Principle of Geography. New York: McGraw-Hill. p. 181.
  3. Snyder, John P. (1989). An Album of Map Projections. Professional Paper 1453. Denver: USGS. p. 238. ISBN 978-0160033681. Retrieved 2014-09-27.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.