Oblique Mercator projection

The oblique Mercator map projection is an adaptation of the standard Mercator projection. The oblique version is sometimes used in national mapping systems. When paired with a suitable geodetic datum, the oblique Mercator delivers high accuracy in zones less than a few degrees in arbitrary directional extent.

oblique Mercator projection.

Standard and oblique aspects
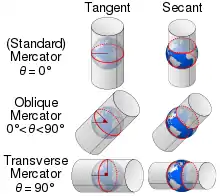
Comparison of tangent and secant forms of normal, oblique and transverse Mercator projections with standard parallels in red

The oblique Mercator projection is the oblique aspect of the standard (or Normal) Mercator projection. They share the same underlying mathematical construction and consequently the oblique Mercator inherits many traits from the normal Mercator:

  • Both projections are cylindrical: for the Normal Mercator, the axis of the cylinder coincides with the polar axis and the line of tangency with the equator. For the transverse Mercator, the axis of the cylinder lies in the equatorial plane, and the line of tangency is any chosen meridian, thereby designated the central meridian.
  • Both projections may be modified to secant forms, which means the scale has been reduced so that the cylinder slices through the model globe.
  • Both exist in spherical and ellipsoidal versions.
  • Both projections are conformal, so that the point scale is independent of direction and local shapes are well preserved;
  • Both projections can have constant scale on the line of tangency (the equator for the normal Mercator and the central meridian for the transverse). For the ellipsoidal form, several developments in use do not have constant scale along the line (which is a geodesic) of tangency.

Since the standard great circle of the oblique Mercator can be chosen at will, it may be used to construct highly accurate maps (of narrow width) anywhere on the globe.

Spherical oblique Mercator

In constructing a map on any projection, a sphere is normally chosen to model the Earth when the extent of the mapped region exceeds a few hundred kilometers in length in both dimensions. For maps of smaller regions, an ellipsoidal model must be chosen if greater accuracy is required; see next section.

Ellipsoidal oblique Mercator

Hotine oblique Mercator projection has approximately constant scale along the geodesic of conceptual tangency.[1] Hotine's work was extended by Engels and Grafarend in 1995 to make the geodesic of conceptual tangency have true scale.[2]

Space-oblique Mercator projection
Main article: Space-oblique Mercator projection

The Space-oblique Mercator projection is a generalization of the oblique Mercator projection to incorporate time evolution of a satellite ground track.

See also

References
  1. Snyder, John P. (1987). Map projections—A Working Manual. U.S. Government Printing Office. p. 70.
  2. Engels, J.; Grafarend, E. (1995). "The oblique Mercator projection of the ellipsoid of revolution". Journal of Geodesy. 70 (1–2): 38–50. doi:10.1007/BF00863417.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.