Faster-than-light

For an earth-bound observer, objects in the sky complete one revolution around the Earth in one day. Proxima Centauri, the nearest star outside the Solar System, is about four light-years away.[6] In this frame of reference, in which Proxima Centauri is perceived to be moving in a circular trajectory with a radius of four light years, it could be described as having a speed many times greater than c as the rim speed of an object moving in a circle is a product of the radius and angular speed.[6] It is also possible on a geostatic view, for objects such as comets to vary their speed from subluminal to superluminal and vice versa simply because the distance from the Earth varies. Comets may have orbits which take them out to more than 1000 AU.[7] The circumference of a circle with a radius of 1000 AU is greater than one light day. In other words, a comet at such a distance is superluminal in a geostatic, and therefore non-inertial, frame.

If a laser beam is swept across a distant object, the spot of laser light can easily be made to move across the object at a speed greater than c.[8] Similarly, a shadow projected onto a distant object can be made to move across the object faster than c.[8] In neither case does the light travel from the source to the object faster than c, nor does any information travel faster than light.[8][9][10]

The rate at which two objects in motion in a single frame of reference get closer together is called the mutual or closing speed. This may approach twice the speed of light, as in the case of two particles travelling at close to the speed of light in opposite directions with respect to the reference frame.

Imagine two fast-moving particles approaching each other from opposite sides of a particle accelerator of the collider type. The closing speed would be the rate at which the distance between the two particles is decreasing. From the point of view of an observer standing at rest relative to the accelerator, this rate will be slightly less than twice the speed of light.

Special relativity does not prohibit this. It tells us that it is wrong to use Galilean relativity to compute the velocity of one of the particles, as would be measured by an observer traveling alongside the other particle. That is, special relativity gives the correct velocity-addition formula for computing such relative velocity.

It is instructive to compute the relative velocity of particles moving at v and −v in accelerator frame, which corresponds to the closing speed of 2v > c. Expressing the speeds in units of c, β = v/c:

${\displaystyle \beta _{\text{rel}}={\frac {\beta +\beta }{1+\beta ^{2}}}={\frac {2\beta }{1+\beta ^{2}}}\leq 1.}$

If a spaceship travels to a planet one light-year (as measured in the Earth's rest frame) away from Earth at high speed, the time taken to reach that planet could be less than one year as measured by the traveller's clock (although it will always be more than one year as measured by a clock on Earth). The value obtained by dividing the distance traveled, as determined in the Earth's frame, by the time taken, measured by the traveller's clock, is known as a proper speed or a proper velocity. There is no limit on the value of a proper speed as a proper speed does not represent a speed measured in a single inertial frame. A light signal that left the Earth at the same time as the traveller would always get to the destination before the traveller.

Since one might not travel faster than light, one might conclude that a human can never travel further from the Earth than 40 light-years if the traveler is active between the age of 20 and 60. A traveler would then never be able to reach more than the very few star systems which exist within the limit of 20–40 light-years from the Earth. This is a mistaken conclusion: because of time dilation, the traveler can travel thousands of light-years during their 40 active years. If the spaceship accelerates at a constant 1 g (in its own changing frame of reference), it will, after 354 days, reach speeds a little under the speed of light (for an observer on Earth), and time dilation will increase the traveler's lifespan to thousands of Earth years, seen from the reference system of the Solar System ⁠— but the traveler's subjective lifespan will not thereby change. If they were then to return to Earth, the traveler would arrive on Earth thousands of years into the future. Their travel speed would not have been observed from Earth as being supraluminal ⁠— neither for that matter would it appear to be so from the traveler's perspective– but the traveler would instead have experienced a length contraction of the universe in their direction of travel. And as the traveler turns around to return, the Earth will seem to experience much more time passing than the traveler does. So while the traveler's (ordinary) coordinate speed cannot exceed c, their proper speed, or distance traveled from the Earth's point of reference divided by proper time, can be much greater than c. This is seen in statistical studies of muons traveling much further than c times their half-life (at rest), if traveling close to c.[11]

The phase velocity of an electromagnetic wave, when traveling through a medium, can routinely exceed c, the vacuum velocity of light. For example, this occurs in most glasses at X-ray frequencies.[12] However, the phase velocity of a wave corresponds to the propagation speed of a theoretical single-frequency (purely monochromatic) component of the wave at that frequency. Such a wave component must be infinite in extent and of constant amplitude (otherwise it is not truly monochromatic), and so cannot convey any information.[13] Thus a phase velocity above c does not imply the propagation of signals with a velocity above c.[14]

The group velocity of a wave may also exceed c in some circumstances.[15][16] In such cases, which typically at the same time involve rapid attenuation of the intensity, the maximum of the envelope of a pulse may travel with a velocity above c. However, even this situation does not imply the propagation of signals with a velocity above c,[17] even though one may be tempted to associate pulse maxima with signals. The latter association has been shown to be misleading, because the information on the arrival of a pulse can be obtained before the pulse maximum arrives. For example, if some mechanism allows the full transmission of the leading part of a pulse while strongly attenuating the pulse maximum and everything behind (distortion), the pulse maximum is effectively shifted forward in time, while the information on the pulse does not come faster than c without this effect.[18] However, group velocity can exceed c in some parts of a Gaussian beam in vacuum (without attenuation). The diffraction causes the peak of the pulse to propagate faster, while overall power does not.[19]

History of the Universe - gravitational waves are hypothesized to arise from cosmic inflation, a faster-than-light expansion just after the Big Bang.[20][21][22]

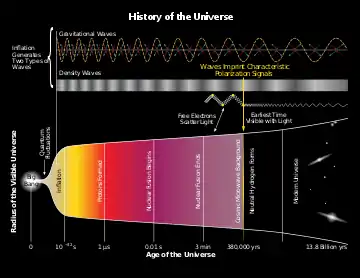
The expansion of the universe causes distant galaxies to recede from us faster than the speed of light, if proper distance and cosmological time are used to calculate the speeds of these galaxies. However, in general relativity, velocity is a local notion, so velocity calculated using comoving coordinates does not have any simple relation to velocity calculated locally.[23] (See Comoving and proper distances for a discussion of different notions of 'velocity' in cosmology.) Rules that apply to relative velocities in special relativity, such as the rule that relative velocities cannot increase past the speed of light, do not apply to relative velocities in comoving coordinates, which are often described in terms of the "expansion of space" between galaxies. This expansion rate is thought to have been at its peak during the inflationary epoch thought to have occurred in a tiny fraction of the second after the Big Bang (models suggest the period would have been from around 10⁻³⁶ seconds after the Big Bang to around 10⁻³³ seconds), when the universe may have rapidly expanded by a factor of around 10²⁰ to 10³⁰.[24]

There are many galaxies visible in telescopes with red shift numbers of 1.4 or higher. All of these are currently traveling away from us at speeds greater than the speed of light. Because the Hubble parameter is decreasing with time, there can actually be cases where a galaxy that is receding from us faster than light does manage to emit a signal which reaches us eventually.[25][26][27]

However, because the expansion of the universe is accelerating, it is projected that most galaxies will eventually cross a type of cosmological event horizon where any light they emit past that point will never be able to reach us at any time in the infinite future,[28] because the light never reaches a point where its "peculiar velocity" towards us exceeds the expansion velocity away from us (these two notions of velocity are also discussed in Comoving and proper distances#Uses of the proper distance). The current distance to this cosmological event horizon is about 16 billion light-years, meaning that a signal from an event happening at present would eventually be able to reach us in the future if the event was less than 16 billion light-years away, but the signal would never reach us if the event was more than 16 billion light-years away.[26]

Apparent superluminal motion is observed in many radio galaxies, blazars, quasars, and recently also in microquasars. The effect was predicted before it was observed by Martin Rees and can be explained as an optical illusion caused by the object partly moving in the direction of the observer,[29] when the speed calculations assume it does not. The phenomenon does not contradict the theory of special relativity. Corrected calculations show these objects have velocities close to the speed of light (relative to our reference frame). They are the first examples of large amounts of mass moving at close to the speed of light.[30] Earth-bound laboratories have only been able to accelerate small numbers of elementary particles to such speeds.

Certain phenomena in quantum mechanics, such as quantum entanglement, might give the superficial impression of allowing communication of information faster than light. According to the no-communication theorem these phenomena do not allow true communication; they only let two observers in different locations see the same system simultaneously, without any way of controlling what either sees. Wavefunction collapse can be viewed as an epiphenomenon of quantum decoherence, which in turn is nothing more than an effect of the underlying local time evolution of the wavefunction of a system and all of its environment. Since the underlying behavior does not violate local causality or allow FTL communication, it follows that neither does the additional effect of wavefunction collapse, whether real or apparent.

The uncertainty principle implies that individual photons may travel for short distances at speeds somewhat faster (or slower) than c, even in vacuum; this possibility must be taken into account when enumerating Feynman diagrams for a particle interaction.[31] However, it was shown in 2011 that a single photon may not travel faster than c.[32] In quantum mechanics, virtual particles may travel faster than light, and this phenomenon is related to the fact that static field effects (which are mediated by virtual particles in quantum terms) may travel faster than light (see section on static fields above). However, macroscopically these fluctuations average out, so that photons do travel in straight lines over long (i.e., non-quantum) distances, and they do travel at the speed of light on average. Therefore, this does not imply the possibility of superluminal information transmission.

There have been various reports in the popular press of experiments on faster-than-light transmission in optics — most often in the context of a kind of quantum tunnelling phenomenon. Usually, such reports deal with a phase velocity or group velocity faster than the vacuum velocity of light.[33][34] However, as stated above, a superluminal phase velocity cannot be used for faster-than-light transmission of information.[35][36]

The Hartman effect is the tunneling effect through a barrier where the tunneling time tends to a constant for large barriers.[37][38] This could, for instance, be the gap between two prisms. When the prisms are in contact, the light passes straight through, but when there is a gap, the light is refracted. There is a non-zero probability that the photon will tunnel across the gap rather than follow the refracted path. For large gaps between the prisms the tunnelling time approaches a constant and thus the photons appear to have crossed with a superluminal speed.[39]

However, the Hartman effect cannot actually be used to violate relativity by transmitting signals faster than c, because the tunnelling time "should not be linked to a velocity since evanescent waves do not propagate".[40] The evanescent waves in the Hartman effect are due to virtual particles and a non-propagating static field, as mentioned in the sections above for gravity and electromagnetism.

In physics, the Casimir–Polder force is a physical force exerted between separate objects due to resonance of vacuum energy in the intervening space between the objects. This is sometimes described in terms of virtual particles interacting with the objects, owing to the mathematical form of one possible way of calculating the strength of the effect. Because the strength of the force falls off rapidly with distance, it is only measurable when the distance between the objects is extremely small. Because the effect is due to virtual particles mediating a static field effect, it is subject to the comments about static fields discussed above.

The EPR paradox refers to a famous thought experiment of Albert Einstein, Boris Podolsky and Nathan Rosen that was realized experimentally for the first time by Alain Aspect in 1981 and 1982 in the Aspect experiment. In this experiment, the measurement of the state of one of the quantum systems of an entangled pair apparently instantaneously forces the other system (which may be distant) to be measured in the complementary state. However, no information can be transmitted this way; the answer to whether or not the measurement actually affects the other quantum system comes down to which interpretation of quantum mechanics one subscribes to.

An experiment performed in 1997 by Nicolas Gisin has demonstrated non-local quantum correlations between particles separated by over 10 kilometers.[41] But as noted earlier, the non-local correlations seen in entanglement cannot actually be used to transmit classical information faster than light, so that relativistic causality is preserved. The situation is akin to sharing a synchronized coin flip, where the second person to flip their coin will always see the opposite of what the first person sees, but neither has any way of knowing whether they were the first or second flipper, without communicating classically. See No-communication theorem for further information. A 2008 quantum physics experiment also performed by Nicolas Gisin and his colleagues has determined that in any hypothetical non-local hidden-variable theory, the speed of the quantum non-local connection (what Einstein called "spooky action at a distance") is at least 10,000 times the speed of light.[42]

The delayed-choice quantum eraser is a version of the EPR paradox in which the observation (or not) of interference after the passage of a photon through a double slit experiment depends on the conditions of observation of a second photon entangled with the first. The characteristic of this experiment is that the observation of the second photon can take place at a later time than the observation of the first photon,[43] which may give the impression that the measurement of the later photons "retroactively" determines whether the earlier photons show interference or not, although the interference pattern can only be seen by correlating the measurements of both members of every pair and so it can't be observed until both photons have been measured, ensuring that an experimenter watching only the photons going through the slit does not obtain information about the other photons in an FTL or backwards-in-time manner.[44][45]

The speed of light

${\displaystyle c={\frac {1}{\sqrt {\varepsilon _{0}\mu _{0}}}}\ }$

is related to the vacuum permittivity ε₀ and the vacuum permeability μ₀. Therefore, not only the phase velocity, group velocity, and energy flow velocity of electromagnetic waves but also the velocity of a photon can be faster than c in a special material that has a constant permittivity or permeability whose value is less than that in vacuum.[51]

Special relativity postulates that the speed of light in vacuum is invariant in inertial frames. That is, it will be the same from any frame of reference moving at a constant speed. The equations do not specify any particular value for the speed of the light, which is an experimentally determined quantity for a fixed unit of length. Since 1983, the SI unit of length (the meter) has been defined using the speed of light.

The experimental determination has been made in vacuum. However, the vacuum we know is not the only possible vacuum which can exist. The vacuum has energy associated with it, called simply the vacuum energy, which could perhaps be altered in certain cases.[52] When vacuum energy is lowered, light itself has been predicted to go faster than the standard value c. This is known as the Scharnhorst effect. Such a vacuum can be produced by bringing two perfectly smooth metal plates together at near atomic diameter spacing. It is called a Casimir vacuum. Calculations imply that light will go faster in such a vacuum by a minuscule amount: a photon traveling between two plates that are 1 micrometer apart would increase the photon's speed by only about one part in 10³⁶.[53] Accordingly, there has as yet been no experimental verification of the prediction. A recent analysis[54] argued that the Scharnhorst effect cannot be used to send information backwards in time with a single set of plates since the plates' rest frame would define a "preferred frame" for FTL signalling. However, with multiple pairs of plates in motion relative to one another the authors noted that they had no arguments that could "guarantee the total absence of causality violations", and invoked Hawking's speculative chronology protection conjecture which suggests that feedback loops of virtual particles would create "uncontrollable singularities in the renormalized quantum stress-energy" on the boundary of any potential time machine, and thus would require a theory of quantum gravity to fully analyze. Other authors argue that Scharnhorst's original analysis, which seemed to show the possibility of faster-than-c signals, involved approximations which may be incorrect, so that it is not clear whether this effect could actually increase signal speed at all.[55]

The physicists Günter Nimtz and Alfons Stahlhofen, of the University of Cologne, claim to have violated relativity experimentally by transmitting photons faster than the speed of light.[39] They say they have conducted an experiment in which microwave photons — relatively low-energy packets of light — travelled "instantaneously" between a pair of prisms that had been moved up to 3 ft (1 m) apart. Their experiment involved an optical phenomenon known as "evanescent modes", and they claim that since evanescent modes have an imaginary wave number, they represent a "mathematical analogy" to quantum tunnelling.[39] Nimtz has also claimed that "evanescent modes are not fully describable by the Maxwell equations and quantum mechanics have to be taken into consideration."[56] Other scientists such as Herbert G. Winful and Robert Helling have argued that in fact there is nothing quantum-mechanical about Nimtz's experiments, and that the results can be fully predicted by the equations of classical electromagnetism (Maxwell's equations).[57][58]

Nimtz told New Scientist magazine: "For the time being, this is the only violation of special relativity that I know of." However, other physicists say that this phenomenon does not allow information to be transmitted faster than light. Aephraim Steinberg, a quantum optics expert at the University of Toronto, Canada, uses the analogy of a train traveling from Chicago to New York, but dropping off train cars from the tail at each station along the way, so that the center of the ever-shrinking main train moves forward at each stop; in this way, the speed of the center of the train exceeds the speed of any of the individual cars.[59]

Winful argues that the train analogy is a variant of the "reshaping argument" for superluminal tunneling velocities, but he goes on to say that this argument is not actually supported by experiment or simulations, which actually show that the transmitted pulse has the same length and shape as the incident pulse.[57] Instead, Winful argues that the group delay in tunneling is not actually the transit time for the pulse (whose spatial length must be greater than the barrier length in order for its spectrum to be narrow enough to allow tunneling), but is instead the lifetime of the energy stored in a standing wave which forms inside the barrier. Since the stored energy in the barrier is less than the energy stored in a barrier-free region of the same length due to destructive interference, the group delay for the energy to escape the barrier region is shorter than it would be in free space, which according to Winful is the explanation for apparently superluminal tunneling.[60][61]

A number of authors have published papers disputing Nimtz's claim that Einstein causality is violated by his experiments, and there are many other papers in the literature discussing why quantum tunneling is not thought to violate causality.[62]

It was later claimed by Eckle et al. that particle tunneling does indeed occur in zero real time.[63] Their tests involved tunneling electrons, where the group argued a relativistic prediction for tunneling time should be 500–600 attoseconds (an attosecond is one quintillionth (10⁻¹⁸) of a second). All that could be measured was 24 attoseconds, which is the limit of the test accuracy. Again, though, other physicists believe that tunneling experiments in which particles appear to spend anomalously short times inside the barrier are in fact fully compatible with relativity, although there is disagreement about whether the explanation involves reshaping of the wave packet or other effects.[60][61][64]

Because of the strong empirical support for special relativity, any modifications to it must necessarily be quite subtle and difficult to measure. The best-known attempt is doubly special relativity, which posits that the Planck length is also the same in all reference frames, and is associated with the work of Giovanni Amelino-Camelia and João Magueijo.[65][66] There are speculative theories that claim inertia is produced by the combined mass of the universe (e.g., Mach's principle), which implies that the rest frame of the universe might be preferred by conventional measurements of natural law. If confirmed, this would imply special relativity is an approximation to a more general theory, but since the relevant comparison would (by definition) be outside the observable universe, it is difficult to imagine (much less construct) experiments to test this hypothesis. Despite this difficulty, such experiments have been proposed.[67]

Although the theory of special relativity forbids objects to have a relative velocity greater than light speed, and general relativity reduces to special relativity in a local sense (in small regions of spacetime where curvature is negligible), general relativity does allow the space between distant objects to expand in such a way that they have a "recession velocity" which exceeds the speed of light, and it is thought that galaxies which are at a distance of more than about 14 billion light-years from us today have a recession velocity which is faster than light.[68] Miguel Alcubierre theorized that it would be possible to create a warp drive, in which a ship would be enclosed in a "warp bubble" where the space at the front of the bubble is rapidly contracting and the space at the back is rapidly expanding, with the result that the bubble can reach a distant destination much faster than a light beam moving outside the bubble, but without objects inside the bubble locally traveling faster than light.[69] However, several objections raised against the Alcubierre drive appear to rule out the possibility of actually using it in any practical fashion. Another possibility predicted by general relativity is the traversable wormhole, which could create a shortcut between arbitrarily distant points in space. As with the Alcubierre drive, travelers moving through the wormhole would not locally move faster than light travelling through the wormhole alongside them, but they would be able to reach their destination (and return to their starting location) faster than light traveling outside the wormhole.

Gerald Cleaver and Richard Obousy, a professor and student of Baylor University, theorized that manipulating the extra spatial dimensions of string theory around a spaceship with an extremely large amount of energy would create a "bubble" that could cause the ship to travel faster than the speed of light. To create this bubble, the physicists believe manipulating the 10th spatial dimension would alter the dark energy in three large spatial dimensions: height, width and length. Cleaver said positive dark energy is currently responsible for speeding up the expansion rate of our universe as time moves on.[70]

The possibility that Lorentz symmetry may be violated has been seriously considered in the last two decades, particularly after the development of a realistic effective field theory that describes this possible violation, the so-called Standard-Model Extension.[71][72][73] This general framework has allowed experimental searches by ultra-high energy cosmic-ray experiments[74] and a wide variety of experiments in gravity, electrons, protons, neutrons, neutrinos, mesons, and photons.[75] The breaking of rotation and boost invariance causes direction dependence in the theory as well as unconventional energy dependence that introduces novel effects, including Lorentz-violating neutrino oscillations and modifications to the dispersion relations of different particle species, which naturally could make particles move faster than light.

In some models of broken Lorentz symmetry, it is postulated that the symmetry is still built into the most fundamental laws of physics, but that spontaneous symmetry breaking of Lorentz invariance[76] shortly after the Big Bang could have left a "relic field" throughout the universe which causes particles to behave differently depending on their velocity relative to the field;[77] however, there are also some models where Lorentz symmetry is broken in a more fundamental way. If Lorentz symmetry can cease to be a fundamental symmetry at the Planck scale or at some other fundamental scale, it is conceivable that particles with a critical speed different from the speed of light be the ultimate constituents of matter.

In current models of Lorentz symmetry violation, the phenomenological parameters are expected to be energy-dependent. Therefore, as widely recognized,[78][79] existing low-energy bounds cannot be applied to high-energy phenomena; however, many searches for Lorentz violation at high energies have been carried out using the Standard-Model Extension.[75] Lorentz symmetry violation is expected to become stronger as one gets closer to the fundamental scale.

In this approach the physical vacuum is viewed as a quantum superfluid which is essentially non-relativistic whereas Lorentz symmetry is not an exact symmetry of nature but rather the approximate description valid only for the small fluctuations of the superfluid background.[80] Within the framework of the approach a theory was proposed in which the physical vacuum is conjectured to be a quantum Bose liquid whose ground-state wavefunction is described by the logarithmic Schrödinger equation. It was shown that the relativistic gravitational interaction arises as the small-amplitude collective excitation mode[81] whereas relativistic elementary particles can be described by the particle-like modes in the limit of low momenta.[82] The important fact is that at very high velocities the behavior of the particle-like modes becomes distinct from the relativistic one - they can reach the speed of light limit at finite energy; also, faster-than-light propagation is possible without requiring moving objects to have imaginary mass.[83][84]

In 2007 the MINOS collaboration reported results measuring the flight-time of 3 GeV neutrinos yielding a speed exceeding that of light by 1.8-sigma significance.[85] However, those measurements were considered to be statistically consistent with neutrinos traveling at the speed of light.[86] After the detectors for the project were upgraded in 2012, MINOS corrected their initial result and found agreement with the speed of light. Further measurements are going to be conducted.[87]

On September 22, 2011, a preprint[88] from the OPERA Collaboration indicated detection of 17 and 28 GeV muon neutrinos, sent 730 kilometers (454 miles) from CERN near Geneva, Switzerland to the Gran Sasso National Laboratory in Italy, traveling faster than light by a relative amount of 2.48×10⁻⁵ (approximately 1 in 40,000), a statistic with 6.0-sigma significance.[89] On 17 November 2011, a second follow-up experiment by OPERA scientists confirmed their initial results.[90][91] However, scientists were skeptical about the results of these experiments, the significance of which was disputed.[92] In March 2012, the ICARUS collaboration failed to reproduce the OPERA results with their equipment, detecting neutrino travel time from CERN to the Gran Sasso National Laboratory indistinguishable from the speed of light.[93] Later the OPERA team reported two flaws in their equipment set-up that had caused errors far outside their original confidence interval: a fiber optic cable attached improperly, which caused the apparently faster-than-light measurements, and a clock oscillator ticking too fast.[94]