Tetrahedrally diminished dodecahedron

In geometry, a tetrahedrally diminished[1] dodecahedron (also tetrahedrally stellated icosahedron or propello tetrahedron[2]) is a topologically self-dual polyhedron made of 16 vertices, 30 edges, and 16 faces (4 equilateral triangles and 12 identical quadrilaterals).[3]

Dorman Luke self-dual form
Tetrahedrally stellated icosahedron
Tetrahedrally diminished dodecahedron
Conway polyhedron notationpT
Faces16: 4 {3} + 12 quadrilaterals
Edges30
Vertices16
Vertex configuration3.4.4.4
4.4.4
Symmetry groupT, [3,3]+, (332), order 12
Dual polyhedronSelf-dual
Propertiesconvex

Nets

A canonical form exists with two edge lengths at 0.849 : 1.057, assuming that the radius of the midsphere is 1. The kites remain isosceles.

It has chiral tetrahedral symmetry, and so its geometry can be constructed from pyritohedral symmetry of the pseudoicosahedron with 4 faces stellated, or from the pyritohedron, with 4 vertices diminished. Within its tetrahedral symmetry, it has geometric varied proportions. By Dorman Luke dual construction, a unique geometric proportion can be defined. The kite faces have edges of length ratio ~ 1:0.633.

Topologically, the triangles are always equilateral, while the quadrilaterals are irregular, although the two adjacent edges that meet at the vertices of a tetrahedron are equal.

As a self-dual hexadecahedron, it is one of 302404 forms, 1476 with at least order 2 symmetry, and the only one with tetrahedral symmetry.[4]

As a diminished regular dodecahedron, with 4 vertices removed, the quadrilaterals faces are trapezoids.

As a stellation of the regular icosahedron it is one of 32 stellations defined with tetrahedral symmetry. It has kite faces.[5]

In Conway polyhedron notation, it can represented as pT, applying George W. Hart's propeller operator to a regular tetrahedron.[6]

This polyhedron represents the vertex figure of a hyperbolic uniform honeycomb, the partially diminished icosahedral honeycomb, pd{3,5,3}, with 12 pentagonal antiprisms and 4 dodecahedron cells meeting at every vertex.

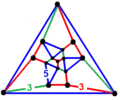
Vertex figure projected as Schlegel diagram

References
  1. It is also less accurately called a tetrahedrally truncated dodecahedron
  2. Sculpture Based on Propellorized Polyhedra
  3. Tetrahedrally Stellated Icosahedron
  4. Self-Dual Hexadecahedra
  5. Tetrahedral Stellations of the Icosahedron
  6. Conway Notation for Polyhedra
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.