Bipyramid
A (symmetric) n-gonal bipyramid or dipyramid is a polyhedron formed by joining an n-gonal pyramid and its mirror image base-to-base.[3][4] An n-gonal bipyramid has 2n triangle faces, 3n edges, and 2 + n vertices.
| "Regular" right (symmetric) n-gonal bipyramids | |
|---|---|
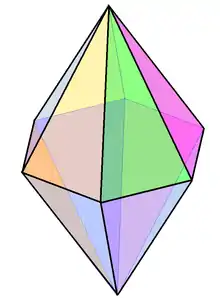 Example "regular" right (symmetric) hexagonal bipyramid | |
| Coxeter diagram | |
| Schläfli symbol | { } + {n}[1] |
| Faces | 2n congruent isosceles triangles |
| Edges | 3n |
| Vertices | 2 + n |
| Face configuration | V4.4.n |
| Symmetry group | Dnh, [n,2], (*n22), order 4n |
| Rotation group | Dn, [n,2]+, (n22), order 2n |
| Dual polyhedron | (convex) uniform ("regular" right) n-gonal prism |
| Properties | convex, face-transitive, regular vertices[2] |
| Net | 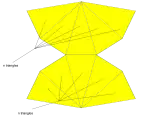 |
The referenced n-gon in the name of a bipyramid is not a face but the internal polygon base, lying in the mirror plane that connects the two pyramid halves. (If it were a face, then each of its edges would connect three faces instead of two.)
"Regular", right bipyramids
A "regular" bipyramid has a regular polygon base. It is usually implied to be also a right bipyramid.
A right bipyramid has its two apexes right above and right below the center or the centroid of its polygon base.
A "regular" right (symmetric) n-gonal bipyramid has Schläfli symbol { } + {n}.
A right (symmetric) bipyramid has Schläfli symbol { } + P, for polygon base P.
The "regular" right (thus face-transitive) n-gonal bipyramid with regular vertices[2] is the dual of the n-gonal uniform (thus right) prism, and has congruent isosceles triangle faces.
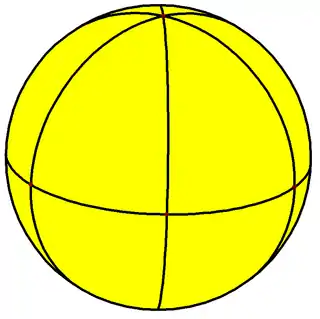
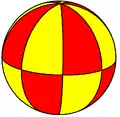
A "regular" right (symmetric) n-gonal bipyramid can be projected on a sphere or globe as a "regular" right (symmetric) n-gonal spherical bipyramid: n equally spaced lines of longitude going from pole to pole, and an equator line bisecting them.
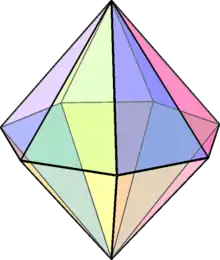
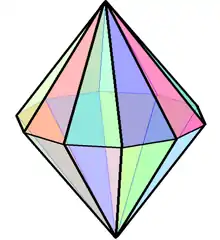
| Name | Digonal bipyramid | Triangular bipyramid (J12) | Square bipyramid (O) | Pentagonal bipyramid (J13) | Hexagonal bipyramid | Heptagonal bipyramid | Octagonal bipyramid | Enneagonal bipyramid | Decagonal bipyramid | ... | Apeirogonal bipyramid |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Polyhedron image | 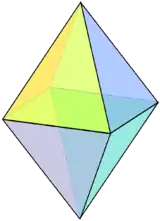 |
 |
 |
 |
 |
 |
... | ||||
| Spherical tiling image |  |
 |
 |
 |
 |
 |
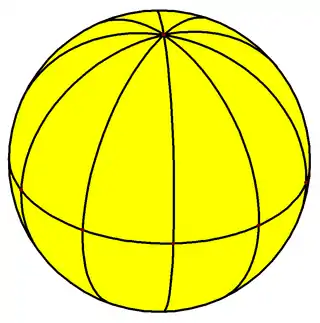 |
Plane tiling image | |||
| Face configuration | V2.4.4 | V3.4.4 | V4.4.4 | V5.4.4 | V6.4.4 | V7.4.4 | V8.4.4 | V9.4.4 | V10.4.4 | ... | V∞.4.4 |
| Coxeter diagram | ... |
Equilateral triangle bipyramids
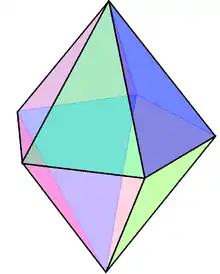
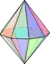
Only three kinds of bipyramids can have all edges of the same length (which implies that all faces are equilateral triangles, and thus the bipyramid is a deltahedron): the "regular" right (symmetric) triangular, tetragonal, and pentagonal bipyramids. The tetragonal or square bipyramid with same length edges, or regular octahedron, counts among the Platonic solids; the triangular and pentagonal bipyramids with same length edges count among the Johnson solids (J12 and J13).
| "Regular" right (symmetric) bipyramid name |
Triangular bipyramid (J12) |
Tetragonal bipyramid (Regular octahedron) |
Pentagonal bipyramid (J13) |
|---|---|---|---|
| Bipyramid image | 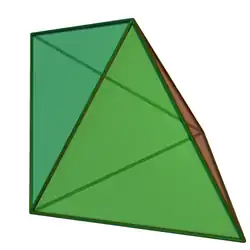 |
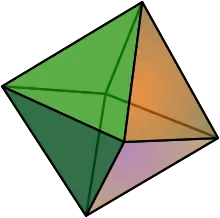 |
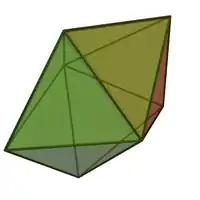 |
Kaleidoscopic symmetry
A "regular" right (symmetric) n-gonal bipyramid has dihedral symmetry group Dnh, of order 4n, except in the case of a regular octahedron, which has the larger octahedral symmetry group Oh, of order 48, which has three versions of D4h as subgroups. The rotation group is Dn, of order 2n, except in the case of a regular octahedron, which has the larger rotation group O, of order 24, which has three versions of D4 as subgroups.
The 4n triangle faces of a "regular" right (symmetric) 2n-gonal bipyramid, projected as the 4n spherical triangle faces of a "regular" right (symmetric) 2n-gonal spherical bipyramid, represent the fundamental domains of dihedral symmetry in three dimensions: Dnh, [n,2], (*n22), order 4n. These domains can be shown as alternately colored spherical triangles:
- in a reflection plane through cocyclic edges, mirror image domains are in different colors (indirect isometry);
- about an n-fold rotation axis through opposite vertices, a domain and its image are in the same color (direct isometry).
An n-gonal (symmetric) bipyramid can be seen as the Kleetope of the "corresponding" n-gonal dihedron.
| Dnh | D1h | D2h | D3h | D4h | D5h | D6h | ... |
|---|---|---|---|---|---|---|---|
| Fundamental domains image |  |
 |
 |
 |
 |
 |
... |
Volume
Volume of a (symmetric) bipyramid:
where B is the area of the base and h the height from the base plane to an apex.
This works for any shape of the base, and for any location of the apex, provided that h is measured as the perpendicular distance from the plane which contains the internal polygon base. Hence:
Volume of a (symmetric) bipyramid whose base is a regular n-sided polygon with side length s and whose height is h:
Oblique bipyramids
Non-right bipyramids are called oblique bipyramids.
Concave bipyramids
A concave bipyramid has a concave polygon base.
 Example concave (symmetric) tetragonal bipyramid (*)
Example concave (symmetric) tetragonal bipyramid (*)
(*) Its base has no obvious centroid; if its apexes are not right above/below the gravity center of its base, it is not a right bipyramid. Anyway, it is a concave octahedron.
Asymmetric/inverted right bipyramids
An asymmetric right bipyramid joins two right pyramids with congruent bases but unequal heights, base-to-base.
An inverted right bipyramid joins two right pyramids with congruent bases but unequal heights, base-to-base, but on the same side of their common base.
The dual of an asymmetric or inverted right bipyramid is a frustum.
A "regular" asymmetric/inverted right n-gonal bipyramid has symmetry group Cnv, of order 2n.
| Asymmetric | Inverted |
|---|---|
 |
 |
Scalene triangle bipyramids
An "isotoxal" right (symmetric) di-n-gonal bipyramid is a right (symmetric) 2n-gonal bipyramid with an isotoxal flat polygon base: its 2n vertices around sides are coplanar, but alternate in two radii.
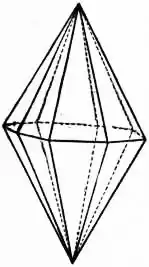 Example ditetragonal bipyramid
Example ditetragonal bipyramid
An "isotoxal" right (symmetric) di-n-gonal bipyramid has n two-fold rotation axes through vertices around sides, n reflection planes through vertices and apexes, an n-fold rotation axis through apexes, a reflection plane through base, and an n-fold rotation-reflection axis through apexes,[4] representing symmetry group Dnh, [n,2], (*22n), of order 4n. (The reflection in base plane corresponds to the 0° rotation-reflection. If n is even, there is a symmetry about the center, corresponding to the 180° rotation-reflection.)
All its faces are congruent scalene triangles, and it is isohedral. It can be seen as another type of right "symmetric" di-n-gonal scalenohedron.
Note: For at most two particular apex heights, triangle faces may be isoceles.
Example:
- The "isotoxal" right (symmetric) "didigonal" (*) bipyramid with base vertices:
- U(1;0;0), U'(-1;0;0), V(0;2;0), V'(0;-2;0),
- and with apexes:
- A(0;0;1), A'(0;0;-1),
- has two different edge lengths:
- ,
- ,
- ;
- thus all its triangle faces are isosceles.
- The "isotoxal" right (symmetric) "didigonal" (*) bipyramid with the same base vertices, but with apex height: 2, also has two different edge lengths: , .
In crystallography, "isotoxal" right (symmetric) "didigonal" (*) (8-faced), ditrigonal (12-faced), ditetragonal (16-faced), and dihexagonal (24-faced) bipyramids exist.[4][3]
(*) The smallest geometric di-n-gonal bipyramids have eight faces, and are topologically identical to the regular octahedron. In this case (2n = 2×2):
an "isotoxal" right (symmetric) "didigonal" bipyramid is called a rhombic bipyramid,[4][3] although all its faces are scalene triangles, because its flat polygon base is a rhombus.
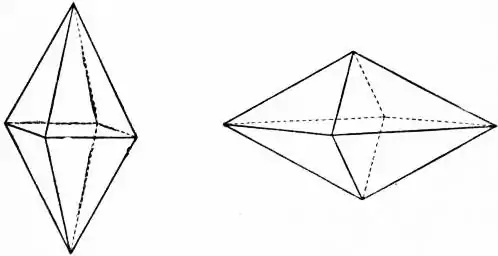 Example rhombic bipyramids
Example rhombic bipyramids
Scalenohedra
A "regular" right "symmetric" di-n-gonal scalenohedron can be made with a regular zig-zag skew 2n-gon base, two symmetric apexes right above and right below the base center, and triangle faces connecting each base edge to each apex.
It has two apexes and 2n vertices around sides, 4n faces, and 6n edges; it is topologically identical to a 2n-gonal bipyramid, but its 2n vertices around sides alternate in two rings above and below the center.[3]
A "regular" right "symmetric" di-n-gonal scalenohedron has n two-fold rotation axes through mid-edges around sides, n reflection planes through vertices and apexes, an n-fold rotation axis through apexes, and an n-fold rotation-reflection axis through apexes,[4] representing symmetry group Dnv = Dnd, [2+,2n], (2*n), of order 4n. (If n is odd, there is a symmetry about the center, corresponding to the 180° rotation-reflection.)
All its faces are congruent scalene triangles, and it is isohedral. It can be seen as another type of right "symmetric" 2n-gonal bipyramid, with a regular zig-zag skew polygon base.
Note: For at most two particular apex heights, triangle faces may be isoceles.
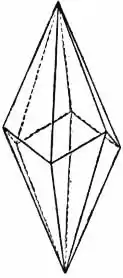 Example ditrigonal scalenohedron
Example ditrigonal scalenohedron
In crystallography, "regular" right "symmetric" "didigonal" (8-faced) and ditrigonal (12-faced) scalenohedra exist.[4][3]
The smallest geometric scalenohedra have eight faces, and are topologically identical to the regular octahedron. In this case (2n = 2×2):
a "regular" right "symmetric" "didigonal" scalenohedron is called a tetragonal scalenohedron;[4][3] its six vertices can be represented as (0,0,±1), (±1,0,z), (0,±1,−z), where z is a parameter between 0 and 1;
at z = 0, it is a regular octahedron; at z = 1, it is a disphenoid with all merged coplanar faces (four congruent isosceles triangles); for z > 1, it becomes concave.
| z = 0.1 | z = 0.25 | z = 0.5 | z = 0.95 | z = 1.5 |
|---|---|---|---|---|
 |
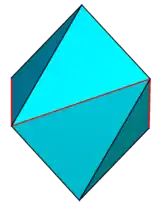 |
 |
 |
 |
 Example disphenoids and 8-faced scalenohedron
Example disphenoids and 8-faced scalenohedron
Note: If the 2n-gon base is both isotoxal in-out and zig-zag skew, then not all triangle faces of the "isotoxal" right "symmetric" solid are congruent.
Example: The solid with isotoxal in-out zig-zag skew 2×2-gon base vertices:
U(1;0;1), U'(-1;0;1), V(0;2;-1), V'(0;-2;-1),
and with "right" symmetric apexes:
A(0;0;3), A'(0;0;-3),
has five different edge lengths:
- ,
- ,
- ,
- ,
- ;
thus not all its triangle faces are congruent.
"Regular" star bipyramids
A self-intersecting or star bipyramid has a star polygon base.
A "regular" right symmetric star bipyramid can be made with a regular star polygon base, two symmetric apexes right above and right below the base center, and thus one-to-one symmetric triangle faces connecting each base edge to each apex.
A "regular" right symmetric star bipyramid has congruent isosceles triangle faces, and is isohedral.
Note: For at most one particular apex height, triangle faces may be equilateral.
A {p/q}-bipyramid has Coxeter diagram ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
| Star polygon base | 5/2-gon | 7/2-gon | 7/3-gon | 8/3-gon | 9/2-gon | 9/4-gon |
|---|---|---|---|---|---|---|
| Star bipyramid image |  |
 |
 |
 |
 |
 |
| Coxeter diagram |
| Star polygon base | 10/3-gon | 11/2-gon | 11/3-gon | 11/4-gon | 11/5-gon | 12/5-gon |
|---|---|---|---|---|---|---|
| Star bipyramid image |  |
 |
 |
 |
 |
 |
| Coxeter diagram |
Scalene triangle star bipyramids
An "isotoxal" right symmetric 2p/q-gonal star bipyramid can be made with an isotoxal in-out star 2p/q-gon base, two symmetric apexes right above and right below the base center, and thus one-to-one symmetric triangle faces connecting each base edge to each apex.
An "isotoxal" right symmetric 2p/q-gonal star bipyramid has congruent scalene triangle faces, and is isohedral. It can be seen as another type of 2p/q-gonal right "symmetric" star scalenohedron.
Note: For at most two particular apex heights, triangle faces may be isoceles.
| Star polygon base | Isotoxal in-out 8/3-gon |
|---|---|
| Scalene triangle star bipyramid image |  |
Star scalenohedra
A "regular" right "symmetric" 2p/q-gonal star scalenohedron can be made with a regular zig-zag skew star 2p/q-gon base, two symmetric apexes right above and right below the base center, and triangle faces connecting each base edge to each apex.
A "regular" right "symmetric" 2p/q-gonal star scalenohedron has congruent scalene triangle faces, and is isohedral. It can be seen as another type of right "symmetric" 2p/q-gonal star bipyramid, with a regular zig-zag skew star polygon base.
Note: For at most two particular apex heights, triangle faces may be isosceles.
| Star polygon base | Regular zig-zag skew 8/3-gon |
|---|---|
| Star scalenohedron image |  |
Note: If the star 2p/q-gon base is both isotoxal in-out and zig-zag skew, then not all triangle faces of the "isotoxal" right "symmetric" star polyhedron are congruent.
| Star polygon base | Isotoxal in-out zig-zag skew 8/3-gon |
|---|---|
| Star polyhedron image |  |
With base vertices:
U0(1;0;1), U1(0;1;1), U2(-1;0;1), U3(0;-1;1),
V0(2;2;-1), V1(-2;2;-1), V2(-2;-2;-1), V3(2;-2;-1),
and with apexes:
A(0;0;3), A'(0;0;-3),
it has four different edge lengths:
- ,
- ,
- ,
- ,
- ;
thus not all its triangle faces are congruent.
4-polytopes with bipyramid cells
The dual of the rectification of each convex regular 4-polytopes is a cell-transitive 4-polytope with bipyramidal cells. In the following, the apex vertex of the bipyramid is A and an equator vertex is E. The distance between adjacent vertices on the equator EE = 1, the apex to equator edge is AE and the distance between the apices is AA. The bipyramid 4-polytope will have VA vertices where the apices of NA bipyramids meet. It will have VE vertices where the type E vertices of NE bipyramids meet. NAE bipyramids meet along each type AE edge. NEE bipyramids meet along each type EE edge. CAE is the cosine of the dihedral angle along an AE edge. CEE is the cosine of the dihedral angle along an EE edge. As cells must fit around an edge, NAA cos−1(CAA) ≤ 2π, NAE cos−1(CAE) ≤ 2π.
| 4-polytope properties | Bipyramid properties | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dual of | Coxeter diagram |
Cells | VA | VE | NA | NE | NAE | NEE | Cell | Coxeter diagram |
AA | AE** | CAE | CEE |
| Rectified 5-cell | 10 | 5 | 5 | 4 | 6 | 3 | 3 | Triangular bipyramid | 2/3 | 0.667 | −1/7 | −1/7 | ||
| Rectified tesseract | 32 | 16 | 8 | 4 | 12 | 3 | 4 | Triangular bipyramid | 0.624 | −2/5 | −1/5 | |||
| Rectified 24-cell | 96 | 24 | 24 | 8 | 12 | 4 | 3 | Triangular bipyramid | 0.745 | 1/11 | −5/11 | |||
| Rectified 120-cell | 1200 | 600 | 120 | 4 | 30 | 3 | 5 | Triangular bipyramid | 0.613 | |||||
| Rectified 16-cell | 24* | 8 | 16 | 6 | 6 | 3 | 3 | Square bipyramid | 1 | −1/3 | −1/3 | |||
| Rectified cubic honeycomb | ∞ | ∞ | ∞ | 6 | 12 | 3 | 4 | Square bipyramid | 1 | 0.866 | −1/2 | 0 | ||
| Rectified 600-cell | 720 | 120 | 600 | 12 | 6 | 3 | 3 | Pentagonal bipyramid | 1.447 | |||||
- * The rectified 16-cell is the regular 24-cell and vertices are all equivalent – octahedra are regular bipyramids.
- ** Given numerically due to more complex form.
Higher dimensions
In general, a bipyramid can be seen as an n-polytope constructed with a (n − 1)-polytope in a hyperplane with two points in opposite directions, equal distance perpendicular from the hyperplane. If the (n − 1)-polytope is a regular polytope, it will have identical pyramidal facets. An example is the 16-cell, which is an octahedral bipyramid, and more generally an n-orthoplex is an (n − 1)-orthoplex bipyramid.
A two-dimensional bipyramid is a square.
See also
References
Citations
- N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite symmetry groups, 11.3 Pyramids, Prisms, and Antiprisms, Figure 11.3c
- "duality". maths.ac-noumea.nc. Retrieved 5 November 2020.
- "The 48 Special Crystal Forms". web.archive.org. 18 September 2013. Retrieved 18 November 2020.
- "Crystal Form, Zones, Crystal Habit". Tulane.edu. Retrieved 16 September 2017.
General references
- Anthony Pugh (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7. Chapter 4: Duals of the Archimedean polyhedra, prisma and antiprisms
External links
| Wikimedia Commons has media related to Bipyramids. |
- Weisstein, Eric W. "Dipyramid". MathWorld.
- Weisstein, Eric W. "Isohedron". MathWorld.
- The Uniform Polyhedra
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
