Trapezohedron
The n-gonal trapezohedron, antidipyramid, antibipyramid, or deltohedron is the dual polyhedron of an n-gonal antiprism. The 2n faces of the n-trapezohedron are symmetrically staggered. With a higher symmetry, its 2n faces are congruent kites (also called deltoids).
| Dual-uniform n-gonal trapezohedra | |
|---|---|
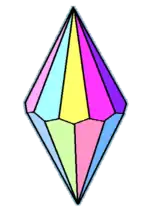 Example dual-uniform decagonal trapezohedron | |
| Type | dual-uniform in the sense of dual-semiregular polyhedron |
| Conway notation | dAn |
| Schläfli symbol | { } ⨁ {n}[1] |
| Coxeter diagrams | |
| Faces | 2n congruent kites |
| Edges | 4n |
| Vertices | 2n + 2 |
| Face configuration | V3.3.3.n |
| Symmetry group | Dnd, [2+,2n], (2*n), order 4n |
| Rotation group | Dn, [2,n]+, (22n), order 2n |
| Dual polyhedron | (convex) uniform n-gonal antiprism |
| Properties | convex, face-transitive, regular vertices[2] |
The n-gon part of the name does not refer to faces here but to two arrangements of vertices around an axis of symmetry. The dual n-gonal antiprism has two actual n-gon faces.
An n-gonal trapezohedron can be dissected into two equal n-gonal pyramids and an n-gonal antiprism.
Name
These figures, sometimes called deltohedra, must not be confused with deltahedra, whose faces are equilateral triangles.
In crystallography, describing the crystal habits of minerals, the word trapezohedron is often used for the polyhedron properly known as a deltoidal icositetrahedron; another polyhedron is known as a deltoid dodecahedron.[3]
Symmetry
The symmetry group of an n-gonal trapezohedron is Dnd of order 4n, except in the case of a cube, which has the larger symmetry group Od of order 48, which has four versions of D3d as subgroups.
The rotation group is Dn of order 2n, except in the case of a cube, which has the larger rotation group O of order 24, which has four versions of D3 as subgroups.
One degree of freedom within symmetry from Dnd (order 4n) to Dn (order 2n) changes the congruent kites into congruent quadrilaterals with three edge lengths, called twisted kites, and the trapezohedron is called a twisted trapezohedron. (In the limit, one edge of each quadrilateral goes to zero length, and the trapezohedron becomes a bipyramid.)
If the kites surrounding the two peaks are not twisted but are of two different shapes, the trapezohedron can only have Cnv (cyclic) symmetry, order 2n, and is called an unequal or asymmetric trapezohedron. Its dual is an unequal antiprism, with the top and bottom polygons of different radii.
If the kites are twisted and are of two different shapes, the trapezohedron can only have Cn (cyclic) symmetry, order n, and is called an unequal twisted trapezohedron.
| Type | Twisted trapezohedron | Unequal trapezohedron | Unequal twisted trapezohedron | |
|---|---|---|---|---|
| Symmetry | Dn, (nn2), [n,2]+ | Cnv, (*nn), [n] | Cn, (nn), [n]+ | |
| Image (n=6) |
 |
 |
 |
 |
| Net | 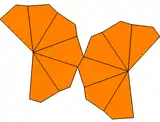 |
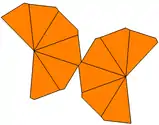 |
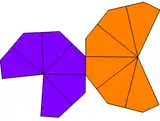 |
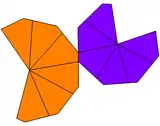 |
Forms
A n-trapezohedron has 2n quadrilateral faces, with 2n+2 vertices. Two vertices are on the polar axis, and the others are in two regular n-gonal rings of vertices.
| Family of n-gonal trapezohedra | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Polyhedron image |  |
 |
 |
 |
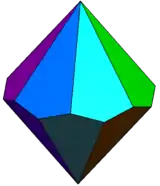 |
 |
 |
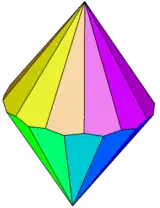 |
... | Apeirogonal trapezohedron | |
| Spherical tiling image | 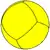 |
 |
 |
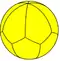 |
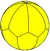 |
 |
 |
 |
Plane tiling image | ||
| Face configuration Vn.3.3.3 | V2.3.3.3 | V3.3.3.3 | V4.3.3.3 | V5.3.3.3 | V6.3.3.3 | V7.3.3.3 | V8.3.3.3 | V10.3.3.3 | V12.3.3.3 | ... | V∞.3.3.3 |
Special cases:
- n=2: A degenerate form of trapezohedron: a geometric tetrahedron with 6 vertices, 8 edges, and 4 degenerate kite faces that are degenerated into triangles. Its dual is a degenerate form of antiprism: also a tetrahedron.
- n=3: In the case of the dual of a triangular antiprism, the kites are rhombi (or squares); hence these trapezohedra are also zonohedra. They are called rhombohedra. They are cubes scaled in the direction of a body diagonal. Also they are the parallelepipeds with congruent rhombic faces.
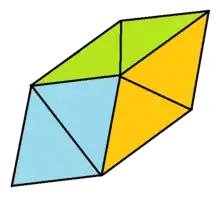 A 60° rhombohedron, dissected into a central regular octahedron and two regular tetrahedra
A 60° rhombohedron, dissected into a central regular octahedron and two regular tetrahedra- A special case of a rhombohedron is one in which the rhombi which form the faces have angles of 60° and 120°. It can be decomposed into two equal regular tetrahedra and a regular octahedron. Since parallelepipeds can fill space, so can a combination of regular tetrahedra and regular octahedra.
Examples
- Crystal arrangements of atoms can repeat in space with trigonal and hexagonal trapezohedral cells.[4]
- The pentagonal trapezohedron is the only polyhedron other than the Platonic solids commonly used as a die in roleplaying games such as Dungeons & Dragons. Having 10 sides, it can be used in repetition to generate any decimal-based uniform probability desired. Two dice of different colors are typically used for the two digits to represent numbers from 00 to 99.
Star trapezohedra
Self-intersecting trapezohedron exist with a star polygon central figure, defined by kite faces connecting each polygon edge to these two points. A p/q-trapezohedron has Coxeter-Dynkin diagram ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
| 5/2 | 5/3 | 7/2 | 7/3 | 7/4 | 8/3 | 8/5 | 9/2 | 9/4 | 9/5 |
|---|---|---|---|---|---|---|---|---|---|
| 10/3 | 11/2 | 11/3 | 11/4 | 11/5 | 11/6 | 11/7 | 12/5 | 12/7 | |
See also
| Wikimedia Commons has media related to Trapezohedra. |
- Diminished trapezohedron
- Rhombic dodecahedron
- Rhombic triacontahedron
- Bipyramid
- Truncated trapezohedron
- Conway polyhedron notation
- The Haunter of the Dark, a short story by H.P. Lovecraft in which a fictional ancient artifact known as The Shining Trapezohedron plays a crucial role.
References
- N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite symmetry groups, 11.3 Pyramids, Prisms, and Antiprisms, Figure 11.3c
- "duality". maths.ac-noumea.nc. Retrieved 2020-10-19.
- "1911 Encyclopædia Britannica/Crystallography - Wikisource, the free online library". en.m.wikisource.org. Retrieved 2020-11-16.
- Trigonal-trapezohedric Class, 3 2 and Hexagonal-trapezohedric Class, 6 2 2
- Anthony Pugh (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7. Chapter 4: Duals of the Archimedean polyhedra, prisma and antiprisms
External links
- Weisstein, Eric W. "Trapezohedron". MathWorld.
- Weisstein, Eric W. "Isohedron". MathWorld.
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- Paper model tetragonal (square) trapezohedron