Beta prime distribution
In probability theory and statistics, the beta prime distribution (also known as inverted beta distribution or beta distribution of the second kind[1]) is an absolutely continuous probability distribution defined for with two parameters α and β, having the probability density function:
|
Probability density function 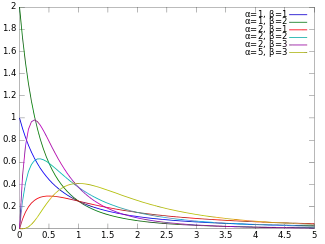 | |||
|
Cumulative distribution function 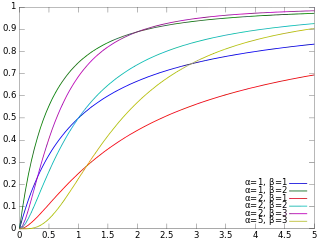 | |||
| Parameters |
shape (real) shape (real) | ||
|---|---|---|---|
| Support | |||
| CDF | where is the incomplete beta function | ||
| Mean | |||
| Mode | |||
| Variance | |||
| Skewness | |||
| MGF | |||
where B is the Beta function.
The cumulative distribution function is
where I is the regularized incomplete beta function.
The expected value, variance, and other details of the distribution are given in the sidebox; for , the excess kurtosis is
While the related beta distribution is the conjugate prior distribution of the parameter of a Bernoulli distribution expressed as a probability, the beta prime distribution is the conjugate prior distribution of the parameter of a Bernoulli distribution expressed in odds. The distribution is a Pearson type VI distribution.[1]
The mode of a variate X distributed as is . Its mean is if (if the mean is infinite, in other words it has no well defined mean) and its variance is if .
For , the k-th moment is given by
For with this simplifies to
The cdf can also be written as
where is the Gauss's hypergeometric function 2F1 .
Generalization
Two more parameters can be added to form the generalized beta prime distribution.
having the probability density function:
with mean
and mode
Note that if p = q = 1 then the generalized beta prime distribution reduces to the standard beta prime distribution
Compound gamma distribution
The compound gamma distribution[2] is the generalization of the beta prime when the scale parameter, q is added, but where p = 1. It is so named because it is formed by compounding two gamma distributions:
where G(x;a,b) is the gamma distribution with shape a and inverse scale b. This relationship can be used to generate random variables with a compound gamma, or beta prime distribution.
The mode, mean and variance of the compound gamma can be obtained by multiplying the mode and mean in the above infobox by q and the variance by q2.
Properties
- If then .
- If then .
- If and two iid variables, then with and , as the beta prime distribution is infinitely divisible.
- More generally, let iid variables following the same beta prime distribution, i.e. , then the sum with and .
Related distributions and properties
- If has an F-distribution, then , or equivalently, .
- If then .
- If and are independent, then .
- Parametrization 1: If are independent, then .
- Parametrization 2: If are independent, then .
- the Dagum distribution
- the Singh–Maddala distribution.
- the log logistic distribution.
- The beta prime distribution is a special case of the type 6 Pearson distribution.
- If X has a Pareto distribution with minimum and shape parameter , then .
- If X has a Lomax distribution, also known as a Pareto Type II distribution, with shape parameter and scale parameter , then .
- If X has a standard Pareto Type IV distribution with shape parameter and inequality parameter , then , or equivalently, .
- The inverted Dirichlet distribution is a generalization of the beta prime distribution.
Notes
- Johnson et al (1995), p 248
- Dubey, Satya D. (December 1970). "Compound gamma, beta and F distributions". Metrika. 16: 27–31. doi:10.1007/BF02613934.
References
- Johnson, N.L., Kotz, S., Balakrishnan, N. (1995). Continuous Univariate Distributions, Volume 2 (2nd Edition), Wiley. ISBN 0-471-58494-0
- MathWorld article