Wrapped exponential distribution
In probability theory and directional statistics, a wrapped exponential distribution is a wrapped probability distribution that results from the "wrapping" of the exponential distribution around the unit circle.
|
Probability density function 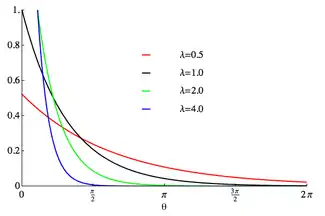 The support is chosen to be [0,2π] | |||
|
Cumulative distribution function 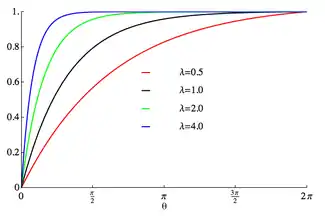 The support is chosen to be [0,2π] | |||
| Parameters | |||
|---|---|---|---|
| Support | |||
| CDF | |||
| Mean | (circular) | ||
| Variance | (circular) | ||
| Entropy | where (differential) | ||
| CF | |||
Definition
The probability density function of the wrapped exponential distribution is[1]
for where is the rate parameter of the unwrapped distribution. This is identical to the truncated distribution obtained by restricting observed values X from the exponential distribution with rate parameter λ to the range .
Characteristic function
The characteristic function of the wrapped exponential is just the characteristic function of the exponential function evaluated at integer arguments:
which yields an alternate expression for the wrapped exponential PDF in terms of the circular variable z=e i (θ-m) valid for all real θ and m:
where is the Lerch transcendent function.
Circular moments
In terms of the circular variable the circular moments of the wrapped exponential distribution are the characteristic function of the exponential distribution evaluated at integer arguments:
where is some interval of length . The first moment is then the average value of z, also known as the mean resultant, or mean resultant vector:
The mean angle is
and the length of the mean resultant is
and the variance is then 1-R.
Characterisation
The wrapped exponential distribution is the maximum entropy probability distribution for distributions restricted to the range for a fixed value of the expectation .[1]
References
- Jammalamadaka, S. Rao; Kozubowski, Tomasz J. (2004). "New Families of Wrapped Distributions for Modeling Skew Circular Data" (PDF). Communications in Statistics - Theory and Methods. 33 (9): 2059–2074. doi:10.1081/STA-200026570. Retrieved 2011-06-13.
