Mølmer–Sørensen gate
The Mølmer–Sørensen gate is a two qubit gate used in quantum computing. It was proposed by Klaus Mølmer and Anders Sørensen.[1] Their proposal also extends to gates on more than two qubits.
| Part of a series on |
| Quantum mechanics |
|---|
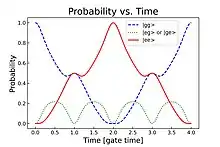
Implementation
To implement the gate, two ions are irradiated with a bichromatic laser field with frequencies , where is the energy splitting of the qubit states and is a detuning close to the motional frequency of the ions. Depending on the interaction time, this produces the states[2]
The above can then be shown to produce a universal set of gates. The Mølmer–Sørensen gate has the advantage that it does not fail if the ions were not cooled completely to the ground state, and it does not require the ions to be individually addressed.[3] However, this thermal insensitivity is only valid in the Lambe Dicke regime, so most implementations first cool the ions to the motional ground state.[4] An experiment was done by P.C. Haljan, K. A. Brickman, L. Deslauriers, P.J. Lee, and C. Monroe where this gate was used to produce all four Bell states and to implement Grover's algorithm successfully.[5]
Interaction Hamiltonian and Evolution
Given that the Mølmer-Sørenson gate only uses a single motional mode of the trapped ions and two of the electronic states to form the qubit, the Hamiltonian of the system for two ions can be expressed as:[1]
where and are the creation and annihilation operators of phonons in the ions collective motional mode, is the energy of those phonons, and is the Pauli z matrix on the th qubit. The Hamiltonian of the system in the interaction picture and with the biochromatic light, after applying the rotating wave approximation, is given by:[4]
where is the Rabi frequency on the qubit carrier transition and is the Lambe Dicke parameter. In the Lamde Dicke regime this Hamiltonian can be approximated and exactly integrated to yield the propagator :[4]
with , and is a displacement operator. So for the displacement operator vanishes and if the gate will be maximally entangle the ions.
References
- Sørensen, Anders; Mølmer, Klaus (March 1, 1999). "Multi-particle entanglement of hot trapped ions". Physical Review Letters. 82 (9): 1835–1838. arXiv:quant-ph/9810040. Bibcode:1999PhRvL..82.1835M. doi:10.1103/PhysRevLett.82.1835.
- Sørensen, Anders; Mølmer, Klaus (March 1, 1999). "Quantum Computation with Ions in Thermal Motion". Physical Review Letters. American Physical Society (APS). 82 (9): 1971–1974. arXiv:quant-ph/9810039. doi:10.1103/physrevlett.82.1971. ISSN 0031-9007.
- HAFFNER, H; ROOS, C; BLATT, R (2008). "Quantum computing with trapped ions". Physics Reports. 469 (4): 155–203. arXiv:0809.4368. Bibcode:2008PhR...469..155H. doi:10.1016/j.physrep.2008.09.003.
- Kirchmair, G; Benhelm, J; Zähringer, F; Gerritsma, R; Roos, C F; Blatt, R (February 4, 2009). "Deterministic entanglement of ions in thermal states of motion". New Journal of Physics. 11 (2): 023002. doi:10.1088/1367-2630/11/2/023002. ISSN 1367-2630.
- Haljan, P. C. (2005). "Spin-Dependent Forces on Trapped Ions for Phase-Stable Quantum Gates and Entangled States of Spin and Motion". Physical Review Letters. 94 (15): 153602. arXiv:quant-ph/0411068. Bibcode:2005PhRvL..94o3602H. doi:10.1103/physrevlett.94.153602. PMID 15904144.