Neutron moderator
In nuclear engineering, a neutron moderator is a medium that reduces the speed of fast neutrons, ideally without capturing any, leaving them as thermal neutrons with only minimal (thermal) kinetic energy. These thermal neutrons are immensely more susceptible than fast neutrons to propagate a nuclear chain reaction of uranium-235 or other fissile isotope by colliding with their atomic nucleus.
| Science with neutrons |
|---|
 |
| Foundations |
| Neutron scattering |
| Other applications |
|
| Infrastructure |
|
| Neutron facilities |
"Light water" is the most commonly used moderator (roughly 75% of the world's reactors) although the term is slightly ambiguous, usually meaning natural fresh water, but could also refer to deuterium-depleted water. Solid graphite (20% of reactors) and heavy water (5% of reactors) are the main alternatives.[1] Beryllium has also been used in some experimental types, and hydrocarbons have been suggested as another possibility.
Moderation
Neutrons are normally bound into an atomic nucleus, and do not exist free for long in nature. The unbound neutron has a half-life of 10 minutes and 11 seconds. The release of neutrons from the nucleus requires exceeding the binding energy of the neutron, which is typically 7-9 MeV for most isotopes. Neutron sources generate free neutrons by a variety of nuclear reactions, including nuclear fission and nuclear fusion. Whatever the source of neutrons, they are released with energies of several MeV.
According to the equipartition theorem, the average kinetic energy, , can be related to temperature, , via:
- ,
where is the neutron mass, is the average squared neutron speed, and is the Boltzmann constant.[2][3] The characteristic neutron temperature of several-MeV neutrons is several tens of billions kelvin.
Moderation is the process of the reduction of the initial high speed (high kinetic energy) of the free neutron. Since energy is conserved, this reduction of the neutron speed takes place by transfer of energy to a material called a moderator.
The probability of scattering of a neutron from a nucleus is given by the scattering cross section. The first couple of collisions with the moderator may be of sufficiently high energy to excite the nucleus of the moderator. Such a collision is inelastic, since some of the kinetic energy is transformed to potential energy by exciting some of the internal degrees of freedom of the nucleus to form an excited state. As the energy of the neutron is lowered, the collisions become predominantly elastic, i.e., the total kinetic energy and momentum of the system (that of the neutron and the nucleus) is conserved.
Given the mathematics of elastic collisions, as neutrons are very light compared to most nuclei, the most efficient way of removing kinetic energy from the neutron is by choosing a moderating nucleus that has near identical mass.

A collision of a neutron, which has mass of 1, with a 1H nucleus (a proton) could result in the neutron losing virtually all of its energy in a single head-on collision. More generally, it is necessary to take into account both glancing and head-on collisions. The mean logarithmic reduction of neutron energy per collision, , depends only on the atomic mass, , of the nucleus and is given by:
.[4]
This can be reasonably approximated to the very simple form .[5] From this one can deduce , the expected number of collisions of the neutron with nuclei of a given type that is required to reduce the kinetic energy of a neutron from to
- .[5]
Choice of moderator materials
Some nuclei have larger absorption cross sections than others, which removes free neutrons from the flux. Therefore, a further criterion for an efficient moderator is one for which this parameter is small. The moderating efficiency gives the ratio of the macroscopic cross sections of scattering, , weighted by divided by that of absorption, : i.e., .[4] For a compound moderator composed of more than one element, such as light or heavy water, it is necessary to take into account the moderating and absorbing effect of both the hydrogen isotope and oxygen atom to calculate . To bring a neutron from the fission energy of 2 MeV to an of 1 eV takes an expected of 16 and 29 collisions for H2O and D2O, respectively. Therefore, neutrons are more rapidly moderated by light water, as H has a far higher . However, it also has a far higher , so that the moderating efficiency is nearly 80 times higher for heavy water than for light water.[4]
The ideal moderator is of low mass, high scattering cross section, and low absorption cross section.
| Hydrogen | Deuterium | Beryllium | Carbon | Oxygen | Uranium | |
|---|---|---|---|---|---|---|
| Mass of kernels u | 1 | 2 | 9 | 12 | 16 | 238 |
| Energy decrement | 1 | 0.7261 | 0.2078 | 0.1589 | 0.1209 | 0.0084 |
| Number of Collisions | 18 | 25 | 86 | 114 | 150 | 2172 |
Distribution of neutron velocities once moderated
After sufficient impacts, the speed of the neutron will be comparable to the speed of the nuclei given by thermal motion; this neutron is then called a thermal neutron, and the process may also be termed thermalization. Once at equilibrium at a given temperature the distribution of speeds (energies) expected of rigid spheres scattering elastically is given by the Maxwell–Boltzmann distribution. This is only slightly modified in a real moderator due to the speed (energy) dependence of the absorption cross-section of most materials, so that low-speed neutrons are preferentially absorbed,[5][6] so that the true neutron velocity distribution in the core would be slightly hotter than predicted.
Reactor moderators
In a thermal-neutron reactor, the nucleus of a heavy fuel element such as uranium absorbs a slow-moving free neutron, becomes unstable, and then splits ("fissions") into two smaller atoms ("fission products"). The fission process for 235U nuclei yields two fission products, two to three fast-moving free neutrons, plus an amount of energy primarily manifested in the kinetic energy of the recoiling fission products. The free neutrons are emitted with a kinetic energy of ~2 MeV each. Because more free neutrons are released from a uranium fission event than thermal neutrons are required to initiate the event, the reaction can become self-sustaining – a chain reaction – under controlled conditions, thus liberating a tremendous amount of energy (see article nuclear fission).
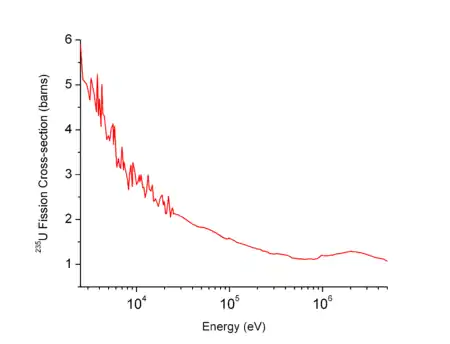
The probability of further fission events is determined by the fission cross section, which is dependent upon the speed (energy) of the incident neutrons. For thermal reactors, high-energy neutrons in the MeV-range are much less likely (though not unable) to cause further fission. The newly released fast neutrons, moving at roughly 10% of the speed of light, must be slowed down or "moderated," typically to speeds of a few kilometres per second, if they are to be likely to cause further fission in neighbouring 235U nuclei and hence continue the chain reaction. This speed happens to be equivalent to temperatures in the few hundred Celsius range.
In all moderated reactors, some neutrons of all energy levels will produce fission, including fast neutrons. Some reactors are more fully thermalised than others; for example, in a CANDU reactor nearly all fission reactions are produced by thermal neutrons, while in a pressurized water reactor (PWR) a considerable portion of the fissions are produced by higher-energy neutrons. In the proposed water-cooled supercritical water reactor (SCWR), the proportion of fast fissions may exceed 50%, making it technically a fast neutron reactor.
A fast reactor uses no moderator, but relies on fission produced by unmoderated fast neutrons to sustain the chain reaction. In some fast reactor designs, up to 20% of fissions can come from direct fast neutron fission of uranium-238, an isotope which is not fissile at all with thermal neutrons.
Moderators are also used in non-reactor neutron sources, such as plutonium-beryllium and spallation sources.
Form and location
The form and location of the moderator can greatly influence the cost and safety of a reactor. Classically, moderators were precision-machined blocks of high purity graphite[7][8] with embedded ducting to carry away heat. They were in the hottest part of the reactor, and therefore subject to corrosion and ablation. In some materials, including graphite, the impact of the neutrons with the moderator can cause the moderator to accumulate dangerous amounts of Wigner energy. This problem led to the infamous Windscale fire at the Windscale Piles, a nuclear reactor complex in the United Kingdom, in 1957.
Some pebble-bed reactors' moderators are not only simple, but also inexpensive: the nuclear fuel is embedded in spheres of reactor-grade pyrolytic carbon, roughly of the size of tennis balls. The spaces between the balls serve as ducting. The reactor is operated above the Wigner annealing temperature so that the graphite does not accumulate dangerous amounts of Wigner energy.
In CANDU and PWR reactors, the moderator is liquid water (heavy water for CANDU, light water for PWR). In the event of a loss-of-coolant accident in a PWR, the moderator is also lost and the reaction will stop. This negative void coefficient is an important safety feature of these reactors. In CANDU the moderator is located in a separate heavy-water circuit, surrounding the pressurized heavy-water coolant channels. This design gives CANDU reactors a positive void coefficient, although the slower neutron kinetics of heavy-water moderated systems compensates for this, leading to comparable safety with PWRs."[9]
Moderator impurities
Good moderators are free of neutron-absorbing impurities such as boron. In commercial nuclear power plants the moderator typically contains dissolved boron. The boron concentration of the reactor coolant can be changed by the operators by adding boric acid or by diluting with water to manipulate reactor power. The Nazi Nuclear Program suffered a substantial setback when its inexpensive graphite moderators failed to function. At that time, most graphites were deposited onto boron electrodes, and the German commercial graphite contained too much boron. Since the war-time German program never discovered this problem, they were forced to use far more expensive heavy water moderators. In the US, Leó Szilárd, a former chemical engineer, discovered the problem.
Non-graphite moderators
Some moderators are quite expensive, for example beryllium, and reactor-grade heavy water. Reactor-grade heavy water must be 99.75% pure to enable reactions with unenriched uranium. This is difficult to prepare because heavy water and regular water form the same chemical bonds in almost the same ways, at only slightly different speeds.
The much cheaper light water moderator (essentially very pure regular water) absorbs too many neutrons to be used with unenriched natural uranium, and therefore uranium enrichment or nuclear reprocessing becomes necessary to operate such reactors, increasing overall costs. Both enrichment and reprocessing are expensive and technologically challenging processes, and additionally both enrichment and several types of reprocessing can be used to create weapons-usable material, causing proliferation concerns. Reprocessing schemes that are more resistant to proliferation are currently under development.
The CANDU reactor's moderator doubles as a safety feature. A large tank of low-temperature, low-pressure heavy water moderates the neutrons and also acts as a heat sink in extreme loss-of-coolant accident conditions. It is separated from the fuel rods that actually generate the heat. Heavy water is very effective at slowing down (moderating) neutrons, giving CANDU reactors their important and defining characteristic of high "neutron economy".
Nuclear weapon design
Early speculation about nuclear weapons assumed that an "atom bomb" would be a large amount of fissile material, moderated by a neutron moderator, similar in structure to a nuclear reactor or "pile".[10] Only the Manhattan project embraced the idea of a chain reaction of fast neutrons in pure metallic uranium or plutonium. Other moderated designs were also considered by the Americans; proposals included using uranium deuteride as the fissile material.[11][12] In 1943 Robert Oppenheimer and Niels Bohr considered the possibility of using a "pile" as a weapon.[13] The motivation was that with a graphite moderator it would be possible to achieve the chain reaction without the use of any isotope separation. In August 1945, when information of the atomic bombing of Hiroshima was relayed to the scientists of the German nuclear program, interred at Farm Hall in England, chief scientist Werner Heisenberg hypothesized that the device must have been "something like a nuclear reactor, with the neutrons slowed by many collisions with a moderator".[14]
After the success of the Manhattan project, all major nuclear weapons programs have relied on fast neutrons in their weapons designs. The notable exception is the Ruth and Ray test explosions of Operation Upshot–Knothole. The aim of the University of California Radiation Laboratory designs was the exploration of deuterated polyethylene charge containing uranium[15]:chapter 15 as a candidate thermonuclear fuel,[16]:203 hoping that deuterium would fuse (becoming an active medium) if compressed appropriately. If successful, the devices could also lead to a compact primary containing minimal amount of fissile material, and powerful enough to ignite RAMROD[16]:149 a thermonuclear weapon designed by UCRL at the time. For a "hydride" primary, the degree of compression would not make deuterium to fuse, but the design could be subjected to boosting, raising the yield considerably.[17]:258 The cores consisted of a mix of uranium deuteride (UD3),[16]:202 and deuterated polyethylene. The core tested in Ray used uranium low enriched in U235, and in both shots deuterium acted as the neutron moderator.[17]:260 The predicted yield was 1.5 to 3 kt for Ruth (with a maximum potential yield of 20 kt[18]:96) and 0.5-1 kt for Ray. The tests produced yields of 200 tons of TNT each; both tests were considered to be fizzles.[11][12]
The main benefit of using a moderator in a nuclear explosive is that the amount of fissile material needed to reach criticality may be greatly reduced. Slowing of fast neutrons will increase the cross section for neutron absorption, reducing the critical mass. A side effect is however that as the chain reaction progresses, the moderator will be heated, thus losing its ability to cool the neutrons.
Another effect of moderation is that the time between subsequent neutron generations is increased, slowing down the reaction. This makes the containment of the explosion a problem; the inertia that is used to confine implosion type bombs will not be able to confine the reaction. The end result may be a fizzle instead of a bang.
The explosive power of a fully moderated explosion is thus limited, at worst it may be equal to a chemical explosive of similar mass. Again quoting Heisenberg: "One can never make an explosive with slow neutrons, not even with the heavy water machine, as then the neutrons only go with thermal speed, with the result that the reaction is so slow that the thing explodes sooner, before the reaction is complete."[19]
While a nuclear bomb working on thermal neutrons may be impractical, modern weapons designs may still benefit from some level of moderation. A beryllium tamper used as a neutron reflector will also act as a moderator.[20][21]
Materials used
- Hydrogen, as in ordinary "light water". Because protium also has a significant cross section for neutron capture only limited moderation is possible without losing too many neutrons. The less-moderated neutrons are relatively more likely to be captured by uranium-238 and less likely to fission uranium-235, so light water reactors require enriched uranium to operate.
- There are also proposals to use the compound formed by the chemical reaction of metallic uranium and hydrogen (uranium hydride—UH3) as a combination fuel and moderator in a new type of reactor.
- Hydrogen is also used in the form of cryogenic liquid methane and sometimes liquid hydrogen as a cold neutron source in some research reactors: yielding a Maxwell–Boltzmann distribution for the neutrons whose maximum is shifted to much lower energies.
- Hydrogen combined with carbon as in paraffin wax was used in some early German experiments.
- Deuterium, in the form of heavy water, in heavy water reactors, e.g. CANDU. Reactors moderated with heavy water can use unenriched natural uranium.
- Carbon, in the form of reactor-grade graphite[7] or pyrolytic carbon, used in e.g. RBMK and pebble-bed reactors, or in compounds, e.g. carbon dioxide. Lower-temperature reactors are susceptible to buildup of Wigner energy in the material. Like deuterium-moderated reactors, some of these reactors can use unenriched natural uranium.
- Graphite is also deliberately allowed to be heated to around 2000 K or higher in some research reactors to produce a hot neutron source: giving a Maxwell–Boltzmann distribution whose maximum is spread out to generate higher energy neutrons.
- Beryllium, in the form of metal. Beryllium is expensive and toxic, so its use is limited.
- Lithium-7, in the form of a lithium fluoride salt, typically in conjunction with beryllium fluoride salt (FLiBe). This is the most common type of moderator in a molten salt reactor.
Other light-nuclei materials are unsuitable for various reasons. Helium is a gas and it requires special design to achieve sufficient density; lithium-6 and boron-10 absorb neutrons.
| Moderator | Reactors | Design | Country |
|---|---|---|---|
| none (fast) | 1 | BN-600 | Russia (1) |
| graphite | 25 | AGR, Magnox, RBMK, UNGG | United Kingdom (14), Russia (11) |
| heavy water | 29 | CANDU PHWR | Canada (17), South Korea (4), Romania (2), China (2), India (18), Argentina, Pakistan |
| light water | 359 | PWR, BWR | 27 countries |
Notes
- Miller, Jr., George Tyler (2002). Living in the Environment: Principles, Connections, and Solutions (12th ed.). Belmont: The Thomson Corporation. p. 345. ISBN 0-534-37697-5.
- Kratz, Jens-Volker; Lieser, Karl Heinrich (2013). Nuclear and Radiochemistry: Fundamentals and Applications (3 ed.). John Wiley & Sons. ISBN 9783527653355. Retrieved 27 April 2018.
- De Graef, Marc; McHenry, Michael E. (2012). Structure of Materials: An Introduction to Crystallography, Diffraction and Symmetry. Cambridge University Press. p. 324. ISBN 9781139560474. Retrieved 27 April 2018.
- Stacey., Weston M (2007). Nuclear reactor physics. Wiley-VCH. pp. 29–31. ISBN 978-3-527-40679-1.
- Dobrzynski, L.; K. Blinowski (1994). Neutrons and Solid State Physics. Ellis Horwood Limited. ISBN 0-13-617192-3.
- Neutron scattering lengths and cross sections V.F. Sears, Neutron News 3, No. 3, 26-37 (1992)
- Arregui Mena, J.D.; et al. (2016). "Spatial variability in the mechanical properties of Gilsocarbon". Carbon. 110: 497–517. doi:10.1016/j.carbon.2016.09.051.
- Arregui Mena, J.D.; et al. (2018). "Characterisation of the spatial variability of material properties of Gilsocarbon and NBG-18 using random fields". Journal of Nuclear Materials. 511: 91–108. doi:10.1016/j.jnucmat.2018.09.008.
- D.A. Meneley and A.P. Muzumdar, "Power Reactor Safety Comparison - a Limited Review", Proceedings of the CNS Annual Conference, June 2009
- Nuclear Weapons Frequently Asked Questions - 8.2.1 Early Research on Fusion Weapons
- Operation Upshot–Knothole
- W48 - globalsecurity.org
- "Atomic Bomb Chronology: 1942-1944". Archived from the original on 2008-05-28. Retrieved 2008-12-16.
- Hans Bethe in Physics Today Vol 53 (2001)
- Herken, Gregg (2003). Brotherhood of the Bomb.
- Hansen, Chuck (1995). Swords of Armageddon. III. Retrieved 2016-12-28.
- Hansen, Chuck (1995). Swords of Armageddon. I. Retrieved 2016-12-28.
- Hansen, Chuck (1995). Swords of Armageddon. VII. Retrieved 2016-12-28.
- Paul Lawrence Rose (1998). Heisenberg and the Nazi Atomic Bomb Project: A Study in German Culture. University of California Press. p. 211. ISBN 978-0-520-21077-6. Retrieved 6 May 2017.
- Nuclear Weapons Frequently Asked Questions - 4.1.7.3.2 Reflectors
- N Moderation
References
- DOE Fundamentals Handbook: Nuclear Physics and Reactor Theory. Vol. 2 (DOE-HDBK-1019/2-93) (PDF). U.S. Department of Energy. January 1993. Archived from the original (PDF) on December 3, 2013. Retrieved November 29, 2013.
