Trigonal trapezohedron

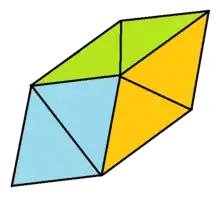
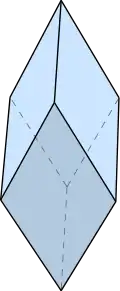
In geometry, a trigonal trapezohedron, or trigonal deltohedron,[1] or isohedral rhombohedron,[2] or rhombic hexahedron[3] is a three-dimensional figure formed by six congruent rhombi.

Trigonal trapezohedron
Typetrapezohedron
Conway notationdA3
Coxeter diagram
Faces6 rhombi
Edges12
Vertices8
Face configuration3,3,3,3
Symmetry groupD3d, [2+,6], (2*3), order 12
Rotation groupD3, [2,3]+, (223), order 6
Dual polyhedrontrigonal antiprism
Propertiesconvex, face-transitive

Six identical rhombic faces can construct two configurations of trigonal trapezohedra. The acute or prolate form has three acute angle corners of the rhombic faces meeting at the two polar axis vertices. The obtuse or oblate or flat form has three obtuse angle corners of the rhombic faces meeting at the two polar axis vertices.

A trigonal trapezohedron is an isohedral rhombohedron. (A general rhombohedron allows up to three types of rhombic faces, three different rhombic angles, with symmetry order 2.)

Geometry

Trigonal trapezohedra are a special kind of parallelepipeds, and are the only parallelepipeds with six congruent faces. Since all edges must have the same length, every trigonal trapezohedron is also a rhombohedron.


A trigonal trapezohedron with square faces is a cube.
A rhombic dodecahedron can be dissected into 4 identical obtuse trigonal trapezohedra.
The rhombic hexecontahedron can be dissected into 20 acute golden rhombohedra meeting at a center point.

Golden rhombohedron

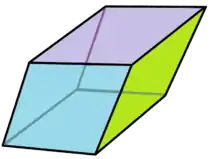Acute form
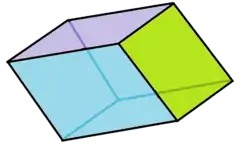Obtuse form

The golden rhombohedra are the two special cases of the trigonal trapezohedron with golden rhombus faces. The acute or prolate form has three acute angle corners of the rhombic faces meeting at the two polar axis vertices. The obtuse or oblate or flat form has three obtuse angle corners of the rhombic faces meeting at the two polar axis vertices.

Asymmetric variation

A lower symmetry variation of the trigonal trapezohedron has only rotational symmetry, D3, and is made from 6 identical irregular quadrilaterals.[4] These quadrilaterals necessarily have two adjacent sides of equal length. This shape is a twisted trapezohedron for n=3.

Polar axis Side Net

A regular octahedron augmented by 2 regular tetrahedra creates a trigonal trapezohedron, with coplanar equilateral triangles merged into 60-degree rhombic faces.

It is the simplest of the trapezohedra, an infinite sequence of polyhedra which are dual to the antiprisms. The dual of a trigonal trapezohedron is a triangular antiprism.

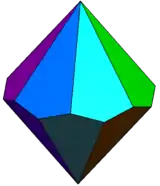
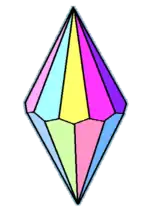
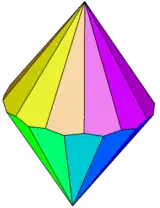
Family of n-gonal trapezohedra
Polyhedron image ... Apeirogonal trapezohedron
Spherical tiling image 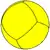Plane tiling image
Face configuration Vn.3.3.3 V2.3.3.3 V3.3.3.3 V4.3.3.3 V5.3.3.3 V6.3.3.3 V7.3.3.3 V8.3.3.3 V10.3.3.3 V12.3.3.3 ... V∞.3.3.3

See also

References
  1. http://mathworld.wolfram.com/TrigonalTrapezohedron.html
  2. Lines, L (1965). Solid geometry: with chapters on space-lattices, sphere-packs and crystals. Dover Publications.
  3. http://www.origamiheaven.com/rhombicpolyhedra.htm
  4. Fair Dice: Trigonal Trapezohedron Asymmetrical sides


This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.