Conway criterion

In the mathematical theory of tessellations, the Conway criterion, named for the English mathematician John Horton Conway, is a fast way to identify many prototiles that tile the plane; it consists of the following requirements:[1] The tile must be a closed topological disk with six consecutive points A, B, C, D, E, and F on the boundary such that:

  • the boundary part from A to B is congruent by translation to the boundary part from E to D
  • each of the boundary parts BC, CD, EF, and FA is centrosymmetric—that is, each one is congruent to itself when rotated by 180-degrees around its midpoint
  • some of the six points may coincide but at least three of them must be distinct.[2]
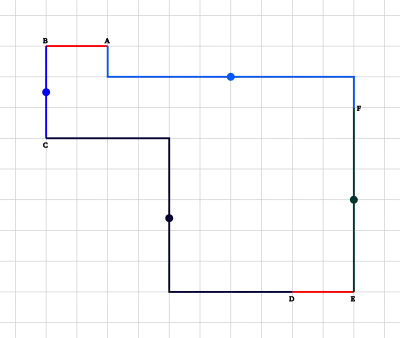
Prototile Octagon satisfying the Conway Criterion. Sections AB and ED are shown in red, and the remaining segments are shown in color with a dot on the point of centrosymmetry.
A tessellation of the above prototile meeting the Conway Criterion.

Any prototile satisfying Conway's criterion admits a periodic tiling of the plane—and does so using only translation and 180-degree rotations. The Conway criterion is a sufficient condition to prove that a prototile tiles the plane but not a necessary one; there are tiles that fail the criterion and still tile the plane.[3]

Examples
A hexagonal tiling with centrosymmetric hexagons
The two nonominoes not satisfying the Conway criterion but able to tile the plane

In its simplest form the criterion states that any hexagon whose opposite sides are parallel and congruent (that is, any hexagonal parallelogon) will tessellate the plane by translation.[4] But when some of the points coincide, the criterion can apply to other polygons and even to shapes with curved perimeters.[5]

The Conway criterion is sufficient, but not necessary, for a shape to tile the plane. For each polyomino up to order 8 that can tile the plane at all, either the polyomino satisfies the Conway criterion or else two copies of the polyomino can be combined to form a polyform patch that satisfies the criterion.[3] The same is true of every tiling nonomino, except for the two tiling nonominoes on the right.[3]

References
  1. Will It Tile? Try the Conway Criterion! by Doris Schattschneider Mathematics Magazine Vol. 53, No. 4 (Sep., 1980), pp. 224-233
  2. Periodic Tiling: Polygons in General
  3. Rhoads, Glenn C. (2005). "Planar tilings by polyominoes, polyhexes, and polyiamonds". Journal of Computational and Applied Mathematics. 174 (2): 329–353. doi:10.1016/j.cam.2004.05.002.
  4. Polyominoes: A Guide to Puzzles and Problems in Tiling, by George Martin, Mathematical Association of America, Washington, DC, 1991, p. 152, ISBN 0883855011
  5. The five types of Conway Criterion polygon tile Archived 2012-07-06 at the Wayback Machine, PDF file
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.