Truchet tiles

In information visualization and graphic design, Truchet tiles are square tiles decorated with patterns that are not rotationally symmetric. When placed in a square tiling of the plane, they can form varied patterns, and the orientation of each tile can be used to visualize information associated with the tile's position within the tiling.[1]

Truchet tiles were first described in a 1704 memoir by Sébastien Truchet entitled "Mémoire sur les combinaisons", and were popularized in 1987 by Cyril Stanley Smith.[1][2]

Variations

Contrasting triangles

The tile originally studied by Truchet is split along the diagonal into two triangles of contrasting colors. The tile has four possible orientations.[3]

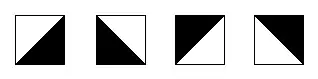
Some examples of surface filling made tiling such a pattern.

With a scheme:

With random placement:

Quarter-circles

A second common form of the Truchet tiles, due to Smith (1987), decorates each tile with two quarter-circles connecting the midpoints of adjacent sides. Each such tile has two possible orientations.

The Truchet tile
Inverse of the Truchet tile, created by any 90° rotation or orthogonal flip

We have such a tiling:

This type of tile has also been used in abstract strategy games Trax and the Black Path Game, prior to Smith's work.[1]

Diagonal

A labyrinth can be generated by tiles in the form of a white square with a black diagonal. As with the quarter-circle tiles, each such tile has two orientations.[4] The connectivity of the resulting labyrinth can be analyzed mathematically using percolation theory as bond percolation at the critical point of a diagonally-oriented grid. Nick Montfort considers the single line of Commodore 64 BASIC required to generate such patterns - 10 PRINT CHR$(205.5+RND(1)); : GOTO 10 - to be "a concrete poem, a found poem".[4]

A labyrinth generated from diagonal tiles

See also

References
  1. Browne, Cameron (2008), "Truchet curves and surfaces", Computers & Graphics, 32 (2): 268–281, doi:10.1016/j.cag.2007.10.001.
  2. Smith, Cyril Stanley (1987), "The tiling patterns of Sebastian Truchet and the topology of structural hierarchy", Leonardo, 20 (4): 373–385, doi:10.2307/1578535. With a translation of Truchet's text by Pauline Boucher.
  3. A New Kind of Science
  4. Montfort, Nick (2012). 10 PRINT CHR$(205.5+RND(1)); : GOTO 10. MIT Press.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.