Hexaoctagonal tiling
In geometry, the hexaoctagonal tiling is a uniform tiling of the hyperbolic plane.
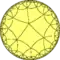
| hexaoctagonal tiling | |
|---|---|
 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic uniform tiling |
| Vertex configuration | (6.8)2 |
| Schläfli symbol | r{8,6} or |
| Wythoff symbol | 8 6 |
| Coxeter diagram |     |
| Symmetry group | [8,6], (*862) |
| Dual | Order-8-6 quasiregular rhombic tiling |
| Properties | Vertex-transitive edge-transitive |
Constructions
There are four uniform constructions of this tiling, three of them as constructed by mirror removal from the [8,6] kaleidoscope. Removing the mirror between the order 2 and 4 points, [8,6,1+], gives [(8,8,3)], (*883). Removing the mirror between the order 2 and 8 points, [1+,8,6], gives [(4,6,6)], (*664). Removing two mirrors as [8,1+,6,1+], leaves remaining mirrors (*4343).
| Uniform Coloring |
|
 |
 |
|
|---|---|---|---|---|
| Symmetry | [8,6] (*862)    |
[(8,3,8)] = [8,6,1+] (*883)   |
[(6,4,6)] = [1+,8,6] (*664)   |
[1+,8,6,1+] (*4343)  |
| Symbol | r{8,6} | r{(8,3,8)} | r{(6,4,6)} | |
| Coxeter diagram |
|
 =  |
= |
= |
Symmetry
The dual tiling has face configuration V6.8.6.8, and represents the fundamental domains of a quadrilateral kaleidoscope, orbifold (*4343), shown here. Adding a 2-fold gyration point at the center of each rhombi defines a (2*43) orbifold. These are subsymmetries of [8,6].
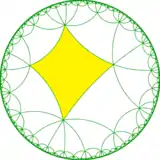 [1+,8,4,1+], (*4343) |
 [(8,4,2+)], (2*43) |
|---|
Related polyhedra and tiling
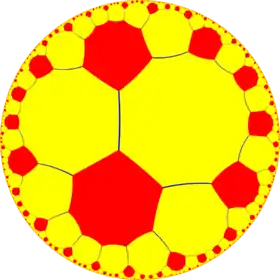
| Uniform octagonal/hexagonal tilings | ||||||
|---|---|---|---|---|---|---|
| Symmetry: [8,6], (*862) | ||||||
|
|
|
|
|
|
|
 |
 |
|
 |
 |
 |
 |
| {8,6} | t{8,6} |
r{8,6} | 2t{8,6}=t{6,8} | 2r{8,6}={6,8} | rr{8,6} | tr{8,6} |
| Uniform duals | ||||||
 |
|
|
|
|
|
|
 |
 |
 |
 |
 |
 |
 |
| V86 | V6.16.16 | V(6.8)2 | V8.12.12 | V68 | V4.6.4.8 | V4.12.16 |
| Alternations | ||||||
| [1+,8,6] (*466) |
[8+,6] (8*3) |
[8,1+,6] (*4232) |
[8,6+] (6*4) |
[8,6,1+] (*883) |
[(8,6,2+)] (2*43) |
[8,6]+ (862) |
 |
 |
|
|
|
|
|
 |
 |
 | ||||
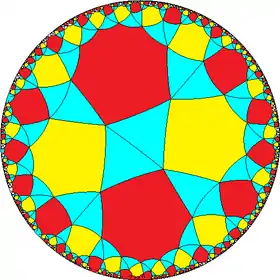| h{8,6} | s{8,6} | hr{8,6} | s{6,8} | h{6,8} | hrr{8,6} | sr{8,6} |
| Alternation duals | ||||||
 |
|
|
|
|
|
|
 |
||||||
| V(4.6)6 | V3.3.8.3.8.3 | V(3.4.4.4)2 | V3.4.3.4.3.6 | V(3.8)8 | V3.45 | V3.3.6.3.8 |
| Symmetry mutation of quasiregular tilings: 6.n.6.n | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry *6n2 [n,6] |
Euclidean | Compact hyperbolic | Paracompact | Noncompact | |||||||
| *632 [3,6] |
*642 [4,6] |
*652 [5,6] |
*662 [6,6] |
*762 [7,6] |
*862 [8,6]... |
*∞62 [∞,6] |
[iπ/λ,6] | ||||
| Quasiregular figures configuration |
 6.3.6.3 |
 6.4.6.4 |
 6.5.6.5 |
 6.6.6.6 |
 6.7.6.7 |
6.8.6.8 |
 6.∞.6.∞ |
6.∞.6.∞ | |||
| Dual figures | |||||||||||
| Rhombic figures configuration |
 V6.3.6.3 |
 V6.4.6.4 |
 V6.5.6.5 |
 V6.6.6.6 |
V6.7.6.7 |
V6.8.6.8 |
 V6.∞.6.∞ |
||||
| Dimensional family of quasiregular polyhedra and tilings: (8.n)2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry *8n2 [n,8] |
Hyperbolic... | Paracompact | Noncompact | ||||||||
| *832 [3,8] |
*842 [4,8] |
*852 [5,8] |
*862 [6,8] |
*872 [7,8] |
*882 [8,8]... |
*∞82 [∞,8] |
[iπ/λ,8] | ||||
| Coxeter |  |
 |
 |
|
 |
|
 |
 | |||
| Quasiregular figures configuration |
 3.8.3.8 |
 4.8.4.8 |
 8.5.8.5 |
8.6.8.6 |
 8.7.8.7 |
 8.8.8.8 |
 8.∞.8.∞ |
8.∞.8.∞ | |||
See also
 |
Wikimedia Commons has media related to Uniform tiling 6-8-6-8. |
- Square tiling
- Tilings of regular polygons
- List of uniform planar tilings
- List of regular polytopes
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
External links
- Weisstein, Eric W. "Hyperbolic tiling". MathWorld.
- Weisstein, Eric W. "Poincaré hyperbolic disk". MathWorld.
- Hyperbolic and Spherical Tiling Gallery
- KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
- Hyperbolic Planar Tessellations, Don Hatch
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.