Dodecagrammic crossed-antiprism
In geometry, the dodecagrammic crossed-antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two dodecagrams.
| Dodecagrammic crossed-antiprism | |
|---|---|
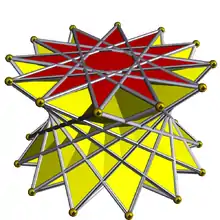 | |
| Type | Uniform polyhedron |
| Faces | 2 {12} 24 {3} |
| Edges | 48 |
| Vertices | 24 |
| Vertex configuration | 12/7.3.3.3 |
| Wythoff symbol | |2 2 12/7 |
| Schläfli symbol | s{2,24/7} |
| Coxeter diagram | |
| Symmetry group | D12d |
| Dual polyhedron | Dodecagrammic concave deltohedron |
| Properties | nonconvex |
Antiprisms are similar to prisms except the bases are twisted relative to each other, and that the side faces are triangles, rather than quadrilaterals. Crossed=antiprism have the triangles crossing the origin.
In the case of a uniform 12/5 base, one usually considers the case where its copy is offset by half'. Extra regularity is obtained by the line connecting the base centers being perpendicular to the base planes, making it a right antiprism. As faces, it has the two dodecagonal bases and, connecting those bases, 24 isosceles triangles.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.