Prismatic uniform polyhedron
In geometry, a prismatic uniform polyhedron is a uniform polyhedron with dihedral symmetry. They exist in two infinite families, the uniform prisms and the uniform antiprisms. All have their vertices in parallel planes and are therefore prismatoids.
Vertex configuration and symmetry groups
Because they are isogonal (vertex-transitive), their vertex arrangement uniquely corresponds to a symmetry group.
The difference between the prismatic and antiprismatic symmetry groups is that Dph has the vertices lined up in both planes, which gives it a reflection plane perpendicular to its p-fold axis (parallel to the {p/q} polygon); while Dpd has the vertices twisted relative to the other plane, which gives it a rotatory reflection. Each has p reflection planes which contain the p-fold axis.
The Dph symmetry group contains inversion if and only if p is even, while Dpd contains inversion symmetry if and only if p is odd.
Enumeration
There are:
- prisms, for each rational number p/q > 2, with symmetry group Dph;
- antiprisms, for each rational number p/q > 3/2, with symmetry group Dpd if q is odd, Dph if q is even.
If p/q is an integer, i.e. if q = 1, the prism or antiprism is convex. (The fraction is always assumed to be stated in lowest terms.)
An antiprism with p/q < 2 is crossed or retrograde; its vertex figure resembles a bowtie. If p/q ≤ 3/2 no uniform antiprism can exist, as its vertex figure would have to violate the triangle inequality.
Images
Note: The tetrahedron, cube, and octahedron are listed here with dihedral symmetry (as a digonal antiprism, square prism and triangular antiprism respectively), although if uniformly colored, the tetrahedron also has tetrahedral symmetry and the cube and octahedron also have octahedral symmetry.
| Symmetry group | Convex | Star forms | ||||||
|---|---|---|---|---|---|---|---|---|
| D2d [2+,2] (2*2) |
 3.3.3 | |||||||
| D3h [2,3] (*223) |
 3.4.4 | |||||||
| D3d [2+,3] (2*3) |
 3.3.3.3 | |||||||
| D4h [2,4] (*224) |
 4.4.4 | |||||||
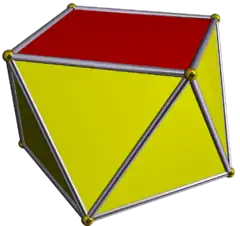
| D4d [2+,4] (2*4) |
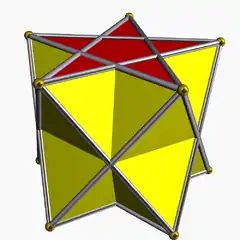
 3.3.3.4 | |||||||
| D5h [2,5] (*225) |
 4.4.5 |
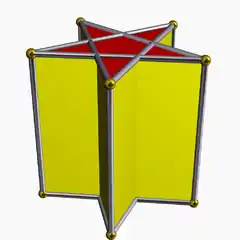 4.4.5⁄2 |
 3.3.3.5⁄2 | |||||
| D5d [2+,5] (2*5) |
 3.3.3.5 |
 3.3.3.5⁄3 | ||||||
| D6h [2,6] (*226) |
 4.4.6 | |||||||
| D6d [2+,6] (2*6) |
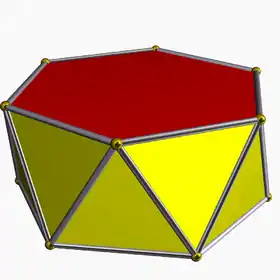 3.3.3.6 | |||||||
| D7h [2,7] (*227) |
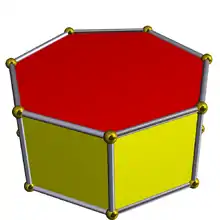 4.4.7 |
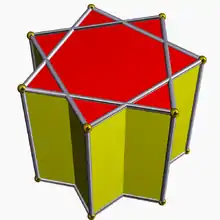 4.4.7⁄2 |
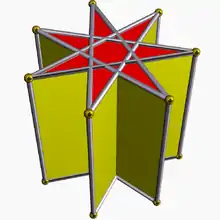 4.4.7⁄3 |
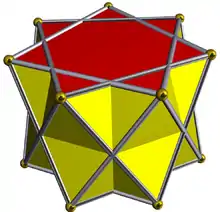 3.3.3.7⁄2 |
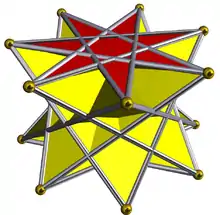 3.3.3.7⁄4 | |||
| D7d [2+,7] (2*7) |
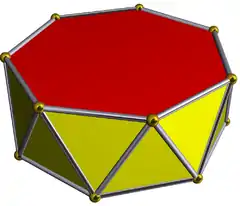 3.3.3.7 |
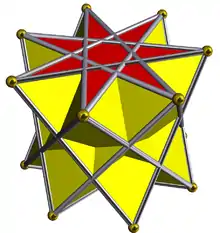 3.3.3.7⁄3 | ||||||
| D8h [2,8] (*228) |
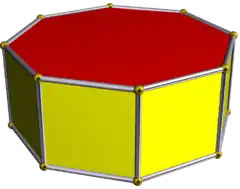 4.4.8 |
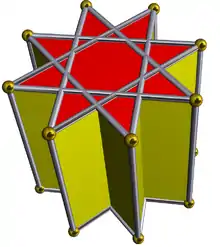 4.4.8⁄3 | ||||||
| D8d [2+,8] (2*8) |
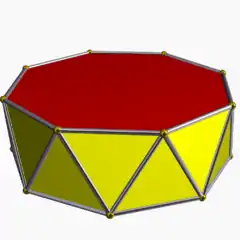 3.3.3.8 |
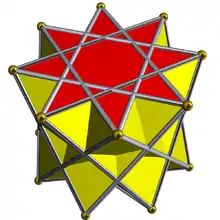 3.3.3.8⁄3 |
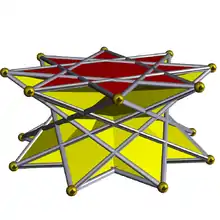 3.3.3.8⁄5 | |||||
| D9h [2,9] (*229) |
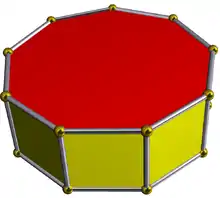 4.4.9 |
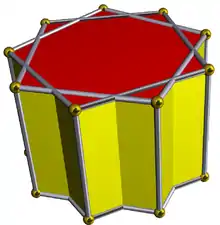 4.4.9⁄2 |
 4.4.9⁄4 |
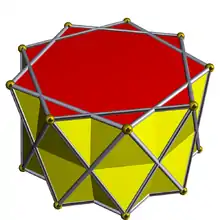 3.3.3.9⁄2 |
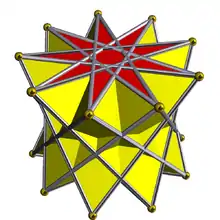 3.3.3.9⁄4 | |||
| D9d [2+,9] (2*9) |
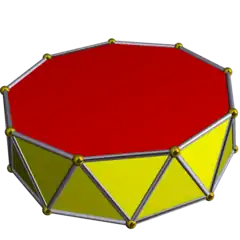 3.3.3.9 |
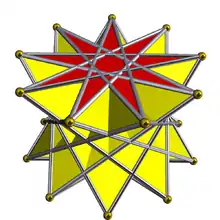 3.3.3.9⁄5 | ||||||
| D10h [2,10] (*2.2.10) |
4.4.10 |
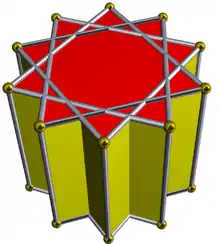 4.4.10⁄3 | ||||||
| D10d [2+,10] (2*10) |
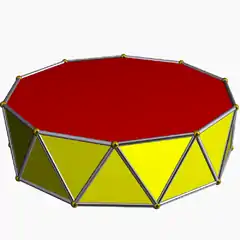 3.3.3.10 |
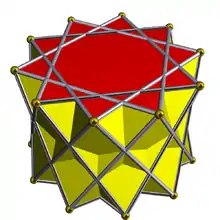 3.3.3.10⁄3 | ||||||
| D11h [2,11] (*2.2.11) |
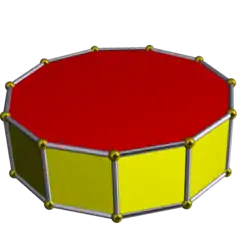 4.4.11 |
 4.4.11⁄2 |
 4.4.11⁄3 |
 4.4.11⁄4 |
 4.4.11⁄5 |
 3.3.3.11⁄2 |
 3.3.3.11⁄4 |
 3.3.3.11⁄6 |
| D11d [2+,11] (2*11) |
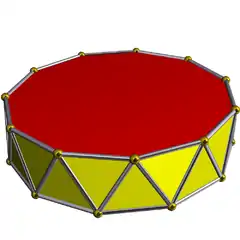 3.3.3.11 |
 3.3.3.11⁄3 |
 3.3.3.11⁄5 |
 3.3.3.11⁄7 | ||||
| D12h [2,12] (*2.2.12) |
 4.4.12 |
 4.4.12⁄5 | ||||||
| D12d [2+,12] (2*12) |
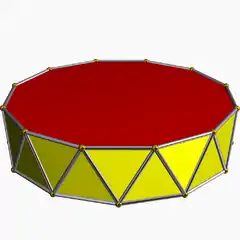 3.3.3.12 |
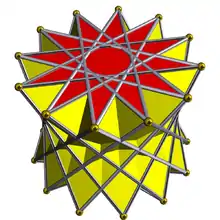 3.3.3.12⁄5 |
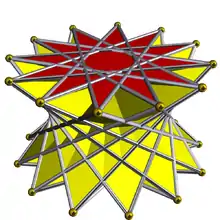 3.3.3.12⁄7 | |||||
| ... | ||||||||
See also
References
- Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954). "Uniform polyhedra". Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. The Royal Society. 246 (916): 401–450. doi:10.1098/rsta.1954.0003. ISSN 0080-4614. JSTOR 91532. MR 0062446.CS1 maint: ref=harv (link)
- Cromwell, P.; Polyhedra, CUP, Hbk. 1997, ISBN 0-521-66432-2. Pbk. (1999), ISBN 0-521-66405-5. p.175
- Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79 (3): 447–457, doi:10.1017/S0305004100052440, MR 0397554.
