Fractint
Fractint is a freeware computer program to render and display many kinds of fractals. The program originated on MS-DOS, then ported to the Atari ST, Linux, and Macintosh. During the early 1990s, Fractint was the definitive fractal generating program for personal computers.[1]
 The Mandelbrot set rendered in Fractint | |
| Developer(s) | Stone Soup Group |
|---|---|
| Initial release | September 1988 |
| Stable release | 20.04p14
/ August 22, 2015 |
| Operating system | MS-DOS, Linux |
| Available in | English |
| Type | Fractal generating software |
| License | Freeware |
| Website | fractint |
The name is a portmanteau of fractal and integer, since the first versions of Fractint used only integer arithmetic (also known as fixed-point arithmetic), for faster rendering on computers without math coprocessors. Since then, floating-point arithmetic and arbitrary-precision arithmetic modes have been added.
Features
FractInt can draw most kinds of fractals that have appeared in the literature. It also has a few "fractal types" that are not strictly speaking fractals, but may be more accurately described as display hacks. These include cellular automata.
History
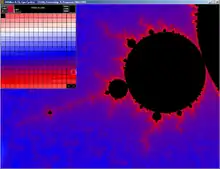

Fractint originally appeared in 1988 as FRACT386, a computer program for rendering fractals very quickly on the Intel 80386 processor using integer arithmetic. Most 386 processors of the era did not come with floating point units (Intel 80387), so the integer approach was much faster.
The early versions of FRACT386 were written by Bert Tyler, who based it on a Mandelbrot generator for a TI-based processor that used integer math and decided to try programming something similar for his 386 machine.[2]
In February 1989, the program was renamed Fractint. In July 1990, it was ported to the Atari ST with the math routines rewritten in Motorola 68000 assembly language by Howard Chu.
See also
| Wikimedia Commons has media related to Fractals created with Fractint. |
References
- Ray Girvan (24 August 1991). "Review: Fractint brought to book". Newscientist. Reed Business Information. Retrieved 25 March 2013.
- Tyler, Bert and Wegner, Timothy, Fractal Creations, 2nd edition, Waite Group Press, 1993, ISBN 1-878739-34-4, p. 461
Further reading
- Michael Frame, Benoît B. Mandelbrot, Fractals, Graphics, and Mathematics Education, Volume 58 of Mathematical Association of America Notes, Cambridge University Press, 2002, ISBN 0-88385-169-5, pp. 57–59 (and used throughout the book)
External links
| Wikibooks has a book on the topic of: Fractals/fractint |



.jpg.webp)

