216 (number)
216 (two hundred [and] sixteen) is the natural number following 215 and preceding 217.
One interpretation of Plato's number
| ||||
|---|---|---|---|---|
[[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] | ||||
| Cardinal | two hundred sixteen | |||
| Ordinal | 216th (two hundred sixteenth) | |||
| Factorization | 23 × 33 | |||
| Divisors | 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 27, 36, 54, 72, 108, 216 | |||
| Greek numeral | ΣΙϚ´ | |||
| Roman numeral | CCXVI | |||
| Binary | 110110002 | |||
| Ternary | 220003 | |||
| Octal | 3308 | |||
| Duodecimal | 16012 | |||
| Hexadecimal | D816 | |||
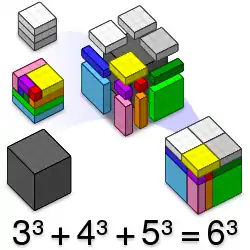
Since 216 = 33 + 43 + 53 = 63, it is the smallest cube that is also the sum of three cubes (Plato was among the first to notice this, and mentioned it in Book VIII of Republic). It is also the sum of a twin prime (107 + 109). But since there is no way to express it as the sum of the proper divisors of any other integer, it is an untouchable number. This multiplicative magic square
has magic constant 216.
It has been conjectured that each natural number not equal to 216 can be written in the form p + Tx, where p is 0 or a prime, and Tx = x(x+1)/2 is a triangular number.[1]
In base 10, it is a Harshad number.
There are 216 fixed hexominoes, the polyominoes made from 6 squares.
216 is a Friedman number.
216 is the smallest number n, for which n−3, n−2, n−1, n+1, n+2, n+3 are all semiprimes.[2]
In other fields
- The 216 colors formed by a 6×6×6 color cube are sometimes known as the web-safe color palette.
- ISO 216 is the ISO's standard for paper sizes.
- 216 is the numerical value of Gevurah, the fifth sephirot in the kabbalistic tree of life, and the sum of the letters in God's 72 hidden names.
- In the film Pi, Max becomes obsessed with a 216-digit number in his quest to find the numeric equation behind existence, and is told by a group of Hasidic Jews that it represents the true name of God.
- According to the Ken Burns series Baseball, it is the number of stitches on a baseball.
- +216 is the country code of Tunisia.
- (216) is the area code of Cleveland, Ohio, United States.
- The Bayon temple in Cambodia has 216 gigantic smiling faces.
See also
- The year 216
References
- Zhi-Wei Sun. "Zhi-Wei Sun's homepage".
- Sloane, N. J. A. (ed.). "Sequence A202319 (Twin semiprime-triples)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- Wells, D. (1987). The Penguin Dictionary of Curious and Interesting Numbers (p. 144). London: Penguin Group.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.