15 (number)

15 (fifteen) is a number, numeral, and glyph. It is the natural number following 14 and preceding 16.

← 14 15 16 →
[[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]]
Cardinalfifteen
Ordinal15th
(fifteenth)
Numeral systempentadecimal
Factorization3 × 5
Divisors1, 3, 5, 15
Greek numeralΙΕ´
Roman numeralXV
Binary11112
Ternary1203
Octal178
Duodecimal1312
HexadecimalF16
Hebrewט"ו (Tet Vav)

Mathematics

15 is:

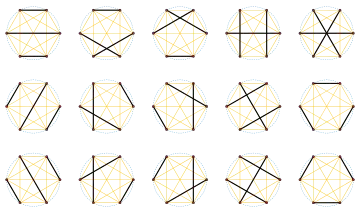
There are 15 perfect matchings of the complete graph K6 and 15 rooted binary trees with four labeled leaves, both of these being among the types of object counted by double factorials. With only two exceptions, all prime quadruplets enclose a multiple of 15, with 15 itself being enclosed by the quadruplet (11, 13, 17, 19).

The 15 perfect matchings of K6

Because 15 is the product of distinct Fermat primes, 3 and 5, a regular polygon with 15 sides is constructible with compass and unmarked straightedge, and cos π/15 is expressible in terms of square roots (see here).

If a positive definite quadratic form with integer matrix represents all positive integers up to 15, then it represents all positive integers via the 15 and 290 theorems.

15 contains the decimal digits 1 and 5, and is the result of adding together the integers from 1 to 5 (1 + 2 + 3 + 4 + 5 = 15)

Science

Religion

Sunnism

The Hanbali Sunni madhab states that the age of fifteen of a solar or lunar calendar is when one's taklif (obligation or responsibility) begins and is the stage whereby one has his deeds recorded.[4]

Judaism

Modern use

15 is designated as an emergency number in Pakistan , for mobile phones, similar to the international GSM emergency number 112; if 112 is used in Pakistan, then the call is routed to 15. 112 can be used in an emergency even if the phone is locked and does not have a SIM card in it.

Sports

Age 15
  • The age of a quinceañera, a Latina girl celebrating her 15th birthday. Thus, Spanish bingo callers might refer to the number 15 as la niña bonita (the beautiful girl).
  • The age for obtaining a driver's (or learner's) permit in certain jurisdictions, including some, where the legal age for a driver's license is 16.
  • In the UK a minor can be sent to prison to await trial at the age of 15.
  • In some countries it is the legal age for sexual intercourse.[5]
  • In the UK it is the legal age to watch a BBFC "15" rated film in a cinema or purchase a "15" rated film or video game.
  • The drinking age in Ethiopia.
  • The age of majority in Indonesia, Myanmar, and Yemen.

Music
  • "Fifteen" is a song composed by Taylor Swift on her album Fearless

In other fields
Fifteen total individuals in the mollusk species Donax variabilis comprise the entire coloration and patterning in their phenotypes.

Fifteen is:

  • The 15 puzzle.
  • The number of minutes in one quarter of an hour; 15 minutes past or before an hour is often known as quarter past and quarter to, respectively.

See also

References
  1. "Sloane's A000384 : Hexagonal numbers". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-01.
  2. "Sloane's A000332 : Binomial coefficient binomial(n,4) = n*(n-1)*(n-2)*(n-3)/24". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-01.
  3. "Sloane's A000110 : Bell or exponential numbers". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-01.
  4. Spevack, Aaron (2011). Ghazali on the Principles of Islamic Spiritualit. p. 50.
  5. Worldwide Ages of Consent. Avert.org. Retrieved on 2011-11-01.

Further reading
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.