34 (number)

34 (thirty-four) is the natural number following 33 and preceding 35.

← 33 34 35 →
[[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]]
Cardinalthirty-four
Ordinal34th
(thirty-fourth)
Factorization2 × 17
Divisors1, 2, 17, 34
Greek numeralΛΔ´
Roman numeralXXXIV
Binary1000102
Ternary10213
Octal428
Duodecimal2A12
Hexadecimal2216

In mathematics

34 is the ninth distinct semiprime and has four divisors including one and itself. Its neighbors, 33 and 35, also are distinct semiprimes, having four divisors each, and 34 is the smallest number to be surrounded by numbers with the same number of divisors as it has.

It is the ninth Fibonacci number[1] and a companion Pell number.[2] Since it is an odd-indexed Fibonacci number, 34 is a Markov number,[3] appearing in solutions with other Fibonacci numbers, such as (1, 13, 34), (1, 34, 89), etc.

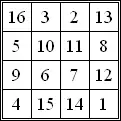
This number is the magic constant of a 4 by 4 normal magic square:[4]

Thirty-four is a heptagonal number.[5]

There is no solution to the equation φ(x) = 34, making 34 a nontotient.[6] Nor is there a solution to the equation x − φ(x) = 34, making 34 a noncototient.[7]

It is a Erdős–Woods number.[8]

In science

Literature

Transportation

In other fields

34 is also:

See also

Rule 34 (Internet meme)

References
  1. "Sloane's A000045 : Fibonacci numbers". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-05-31.
  2. "Sloane's A002203 : Companion Pell numbers". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-05-31.
  3. Weisstein, Eric W. "Markov Number". mathworld.wolfram.com. Retrieved 2020-08-21.
  4. Higgins, Peter (2008). Number Story: From Counting to Cryptography. New York: Copernicus. p. 53. ISBN 978-1-84800-000-1.
  5. "Sloane's A000566 : Heptagonal numbers". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-05-31.
  6. "Sloane's A005277 : Nontotients". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-05-31.
  7. "Sloane's A005278 : Noncototients". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-05-31.
  8. "Sloane's A059756 : Erdős–Woods numbers". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2020-12-04.
  9. "Evidence for a new nuclear 'magic number'" (Press release). Saitama, Japan: Riken. 2013-10-10. Retrieved 2013-10-14.
  10. Steppenbeck, D.; Takeuchi, S.; Aoi, N.; et al. (2013-10-10). "Evidence for a new nuclear 'magic number' from the level structure of 54Ca". Nature. 502 (7470): 207–210. doi:10.1038/nature12522. PMID 24108051.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.