Symmetry in biology
Symmetry in biology refers to the symmetry observed in organisms, including plants, animals, fungi, and bacteria. External symmetry can be easily seen by just looking at an organism. For example, take the face of a human being which has a plane of symmetry down its centre, or a pine cone with a clear symmetrical spiral pattern. Internal features can also show symmetry, for example the tubes in the human body (responsible for transporting gases, nutrients, and waste products) which are cylindrical and have several planes of symmetry.


Biological symmetry can be thought of as a balanced distribution of duplicate body parts or shapes within the body of an organism. Importantly, unlike in mathematics, symmetry in biology is always approximate. For example, plant leaves – while considered symmetrical – rarely match up exactly when folded in half. Symmetry is one class of patterns in nature whereby there is near-repetition of the pattern element, either by reflection or rotation.
While sponges and placozoans represent two groups of animals which don't show any symmetry (i.e. are asymmetrical), the body plans of most multicellular organisms exhibit, and are defined by, some form of symmetry. There are only a few types of symmetry which are possible in body plans. These are radial (cylindrical), bilateral, biradial and spherical symmetry.[1] While the classification of viruses as an 'organism' remains controversial, viruses also contain icosahedral symmetry.
The importance of symmetry is illustrated by the fact that groups of animals have traditionally been defined by this feature in taxonomic groupings. The Radiata, animals with radial symmetry, formed one of the four branches of Georges Cuvier's classification of the animal kingdom.[2][3][4] Meanwhile, Bilateria is a taxonomic grouping still used today to represent organisms with embryonic bilateral symmetry.
Radial symmetry
Organisms with radial symmetry show a repeating pattern around a central axis such that they can be separated into several identical pieces when cut through the central point, much like pieces of a pie. Typically, this involves repeating a body part 4, 5, 6 or 8 times around the axis – referred to as tetramerism, pentamerism, hexamerism and octomerism, respectively. Such organisms exhibits no left or right sides but do have a top and a bottom surface, or a front and a back.
George Cuvier classified animals with radial symmetry in the taxon Radiata (Zoophytes),[5][6] which is now generally accepted to be an assemblage of different animal phyla that do not share a single common ancestor (a polyphyletic group).[7] Most radially symmetric animals are symmetrical about an axis extending from the center of the oral surface, which contains the mouth, to the center of the opposite (aboral) end. Animals in the phyla Cnidaria and Echinodermata generally show radial symmety,[8] although many sea anemones and some corals within the Cnidaria have bilateral symmetry defined by a single structure, the siphonoglyph.[9] Radial symmetry is especially suitable for sessile animals such as the sea anemone, floating animals such as jellyfish, and slow moving organisms such as starfish; whereas bilateral symmetry favours locomotion by generating a streamlined body.
Many flowers are also radially symmetric, or 'actinomorphic'. Roughly identical floral structures – petals, sepals, and stamens – occur at regular intervals around the axis of the flower, which is often the female reproductive organ containing the carpel, style and stigma.[10]

Subtypes of radial symmetry
Some jellyfish, such as Aurelia marginalis, show tetramerism with a four-fold radial symmetry. This is immediately obvious when looking at the jellyfish due to the presence of four gonads, visible through its translucent body. This radial symmetry is ecologically important in allowing the jellyfish to detect and respond to stimuli (mainly food and danger) from all directions.

Flowering plants show five-fold symmetry, or pentamerism, in many of their flowers and fruits. This is easily seen through the arrangement of five carpels (seed pockets) in an apple when cut transversely. Among animals, only the echinoderms such as sea stars, sea urchins, and sea lilies are pentamerous as adults, with five arms arranged around the mouth. Being bilaterian animals, however, they initially develop with mirror symmetry as larvae, then gain pentaradial symmetry later.[11]
Hexamerism is found in the corals and sea anemones (class Anthozoa) that are divided into two groups based on their symmetry. The most common corals in the subclass Hexacorallia have a hexameric body plan; their polyps have six-fold internal symmetry and a number of tentacles that is a multiple of six.
Octamerism is found in corals of the subclass Octocorallia. These have polyps with eight tentacles and octameric radial symmetry. The octopus, however, has bilateral symmetry, despite its eight arms.
Icosahedral symmetry
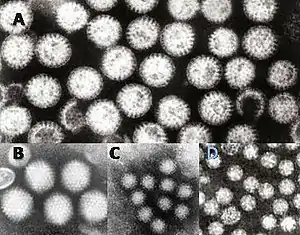
Icosahedral symmetry occurs in an organism which contains 60 subunits generated by 20 faces, each an equilateral triangle, and 12 corners. Within the icosahedron there is 2-fold, 3-fold and 5-fold symmetry. Many viruses, including canine parvovirus, show this form of symmetry due to the presence of an icosahedral viral shell. Such symmetry has evolved because it allows the viral particle to be built up of repetitive subunits consisting of a limited number of structural proteins (encoded by viral genes), thereby saving space in the viral genome. The icosahedral symmetry can still be maintained with more than 60 subunits, but only in factors of 60. For example, the T=3 Tomato bushy stunt virus has 60x3 protein subunits (180 copies of the same structural protein).[12][13] Although these viruses are often referred to as 'spherical', they do not show true mathematical spherical symmetry.
In the early 20th century, Ernst Haeckel described (Haeckel, 1904) a number of species of Radiolaria, some of whose skeletons are shaped like various regular polyhedra. Examples include Circoporus octahedrus, Circogonia icosahedra, Lithocubus geometricus and Circorrhegma dodecahedra. The shapes of these creatures should be obvious from their names. Tetrahedral symmetry is present in Callimitra agnesae.
Spherical symmetry
Spherical symmetry is characterised by the ability to draw an endless, or great but finite, number of symmetry axes through the body. This means that spherical symmetry occurs in an organism if it is able to be cut into two identical halves through any cut that runs through the organism's center. True spherical symmetry is not found in animal body plans.[14] Organisms which show approximate spherical symmetry include the freshwater green alga Volvox.[8]
Bacteria are often referred to as having a 'spherical' shape. Bacteria are categorized based on their shapes into three classes: cocci (spherical-shaped), bacillus (rod-shaped) and spirochetes (spiral-shaped) cells. In reality, this is a severe over-simplification as bacterial cells can be curved, bent, flattened, oblong spheroids and many more shapes.[15] Due to the huge number of bacteria considered to be cocci (coccus if a single cell), it is unlikely that all of these show true spherical symmetry. It is important to distinguish between the generalized use of the word 'spherical' to describe organisms at ease, and the true meaning of spherical symmetry. The same situation is seen in the description of viruses – 'spherical' viruses do not necessarily show spherical symmetry, usually they are icosahedral.
Bilateral symmetry
Organisms with bilateral symmetry contain a single plane of symmetry, the sagittal plane, which divides the organism into two roughly mirror image left and right halves – approximate reflectional symmetry.

.jpg.webp)
Animals with bilateral symmetry are classified into a large group called the bilateria which contains 99% of all animals (comprising over 32 phyla and 1 million described species). All bilaterians have some asymmetrical features; for example, the human heart and liver are positioned asymmetrically despite the body having external bilateral symmetry.[16]
The bilateral symmetry of bilaterians is a complex trait which develops due to the expression of many genes. The bilateria have two axes of polarity. The first is an anterior-posterior (AP) axis which can be visualised as an imaginary axis running from the head or mouth to the tail or other end of an organism. The second is the dorsal-ventral (DV) axis which runs perpendicular to the AP axis.[17][18] During development the AP axis is always specified before the DV axis.[19]
The AP axis is essential in defining the polarity of bilateria and allowing the development of a front and back to give the organism direction. The front end encounters the environment before the rest of the body so sensory organs such as eyes tend to be clustered there. This is also the site where a mouth develops since it is the first part of the body to encounter food. Therefore, a distinct head, with sense organs connected to a central nervous system, tends to develop.[20] This pattern of development (with a distinct head and tail) is called cephalization. It is also argued that the development of an AP axis is important in locomotion - bilateral symmetry gives the body an intrinsic direction and allows streamlining to reduce drag.
In addition to animals, the flowers of some plants also show bilateral symmetry. Such plants are referred to as zygomorphic and include the orchid (Orchidaceae) and pea (Fabaceae) families, and most of the figwort family (Scrophulariaceae).[21][22] The leaves of plants also commonly show approximate bilateral symmetry.
Biradial symmetry
Biradial symmetry is found in organisms which show morphological features (internal or external) of both bilateral and radial symmetry. Unlike radially symmetrical organisms which can be divided equally along many planes, biradial organisms can only be cut equally along two planes. This could represent an intermediate stage in the evolution of bilateral symmetry from a radially symmetric ancestor.[23]
The animal group with the most obvious biradial symmetry is the ctenophores. In ctenophores the two planes of symmetry are (1) the plane of the tentacles and (2) the plane of the pharynx.[24] In addition to this group, evidence for biradial symmetry has even been found in the 'perfectly radial' freshwater polyp Hydra (a cnidarian). Biradial symmetry, especially when considering both internal and external features, is more common than originally accounted for.[25]
Evolution of symmetry
Like all the traits of organisms, symmetry (or indeed asymmetry) evolves due to an advantage to the organism - a process of natural selection. This involves changes in the frequency of symmetry-related genes throughout time.
Evolution of symmetry in plants
Early flowering plants had radially symmetric flowers but since then many plants have evolved bilaterally symmetrical flowers. The evolution of bilateral symmetry is due to the expression of CYCLOIDEA genes. Evidence for the role of the CYCLOIDEA gene family comes from mutations in these genes which cause a reversion to radial symmetry. The CYCLOIDEA genes encode transcription factors, proteins which control the expression of other genes. This allows their expression to influence developmental pathways relating to symmetry.[26][27] For example, in Antirrhinum majus, CYCLOIDEA is expressed during early development in the dorsal domain of the flower meristem and continues to be expressed later on in the dorsal petals to control their size and shape. It is believed that the evolution of specialized pollinators may play a part in the transition of radially symmetrical flowers to bilaterally symmetrical flowers.[28]
Evolution of symmetry in animals
Symmetry is often selected for in the evolution of animals. This is unsurprising since asymmetry is often an indication of unfitness - either defects during development or injuries throughout a lifetime. This is most apparent during mating during which females of some species select males with highly symmetrical features. For example, facial symmetry influences human judgements of human attractiveness.[29] Additionally, female barn swallows, a species where adults have long tail streamers, prefer to mate with males that have the most symmetrical tails.[30]
While symmetry is known to be under selection, the evolutionary history of different types of symmetry in animals is an area of extensive debate. Traditionally it has been suggested that bilateral animals evolved from a radial ancestor. Cnidarians, a phylum containing animals with radial symmetry, are the most closely related group to the bilaterians. Cnidarians are one of two groups of early animals considered to have defined structure, the second being the ctenophores. Ctenophores show biradial symmetry leading to the suggestion that they represent an intermediate step in the evolution of bilateral symmetry from radial symmetry.[31]
Interpretations based only on morphology are not sufficient to explain the evolution of symmetry. Two different explanations are proposed for the different symmetries in cnidarians and bilateria. The first suggestion is that an ancestral animal had no symmetry (was asymmetric) before cnidarians and bilaterians separated into different evolutionary lineages. Radial symmetry could have then evolved in cnidarians and bilateral symmetry in bilaterians. Alternatively, the second suggestion is that an ancestor of cnidarians and bilaterians had bilateral symmetry before the cnidarians evolved and became different by having radial symmetry. Both potential explanations are being explored and evidence continues to fuel the debate.
Asymmetry
Although asymmetry is typically associated with being unfit, some species have evolved to be asymmetrical as an important adaptation. Many members of the phylum Porifera (sponges) have no symmetry, though some are radially symmetric.[32]
| Group/Species | Asymmetrical Feature | Adaptive Benefit |
|---|---|---|
| Some owls[33] | Size and positioning of ears | Allows the owl to more precisely determine the location of prey |
| Flatfish[34] | Both eyes on the same side of their head | Rest and swim on one side (to blend in with sand floor of the ocean) |
| The scale-eating cichlid Perissodus microlepis[35] | Mouth and jaw asymmetry | More effective at removing scales from their prey |
| Humans[36][37][38] | Handedness and internal asymmetry of organs e.g. left lung is smaller than the right | Handedness is an adaptation reflecting the asymmetries of the human brain. Internal asymmetry contributes to positioning and generation of a functional system. |
 Head of a male crossbill showing asymmetrical upper and lower beak
Head of a male crossbill showing asymmetrical upper and lower beak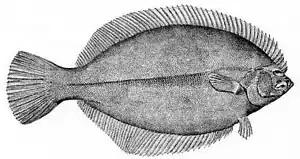 A winter flounder, a type of flatfish, with both eyes on the top of its head
A winter flounder, a type of flatfish, with both eyes on the top of its head Hermit crabs have different sized claws
Hermit crabs have different sized claws A Roman snail and its helical shell
A Roman snail and its helical shell Chicoreus palmarosae, a sea snail, illustrating asymmetry which is seen in all gastropods in the form of a helical shell
Chicoreus palmarosae, a sea snail, illustrating asymmetry which is seen in all gastropods in the form of a helical shell A red slug, clearly showing the pneumostome
A red slug, clearly showing the pneumostome.jpg.webp)
Symmetry breaking
The presence of these asymmetrical features requires a process of symmetry breaking during development, both in plants and animals. Symmetry breaking occurs at several different levels in order to generate the anatomical asymmetry which we observe. These levels include asymmetric gene expression, protein expression, and activity of cells.
For example, left-right asymmetry in mammals has been investigated extensively in the embryos of mice. Such studies have led to support for the nodal flow hypothesis. In a region of the embryo referred to as the node there are small hair-like structures (monocilia) which all rotate together in a particular direction. This creates a unidirectional flow of signalling molecules causing these signals to accumulate on one side of the embryo and not the other. This results in the activation of different developmental pathways on each side, and subsequent asymmetry.[40][41]

Much of the investigation of the genetic basis of symmetry breaking has been done on chick embryos. In chick embryos the left side expresses genes called NODAL and LEFTY2 which activate PITX2 to signal the development of left side structures. Whereas, the right side does not express PITX2 and consequently develops right side structures.[42][43] A more complete pathway is shown in the image at the side of the page.
For more information about symmetry breaking in animals please refer to the left-right asymmetry page.
Plants also show asymmetry. For example the direction of helical growth in Arabidopsis, the most commonly studied model plant, shows left-handedness. Interestingly, the genes involved in this asymmetry are similar (closely related) to those in animal asymmetry – both LEFTY1 and LEFTY2 play a role. In the same way as animals, symmetry breaking in plants can occur at a molecular (genes/proteins), subcellular, cellular, tissue and organ level.[44]
See also
Biological structures
References
Citations
- Holló, Gábor (2015). "A new paradigm for animal symmetry". Interface Focus. 5 (6): 20150032. doi:10.1098/rsfs.2015.0032. PMID 26640644.
- McBirney, Alexander (2009). Georges Cuvier. In: The Philosophy of Zoology Before Darwin. Springer, Dordrecht. p. 87-98.
- Waggoner, Ben M. "Georges Cuvier (1769–1832)". UCMP Berkeley. Retrieved 8 March 2018.
Cuvier's insistence on the functional integration of organisms led him to classify animals into four "branches," or embranchements: Vertebrata, Articulata (arthropods and segmented worms), Mollusca (which at the time meant all other soft, bilaterally symmetrical invertebrates), and Radiata (cnidarians and echinoderms).
- Cuvier, Georges; Griffith, Edward; Pidgeon, Edward (1834). The Mollusca and Radiata: Arranged by the Baron Cuvier, with Supplementary Additions to Each Order. Whittaker and Company. pp. 435–.
- Waggoner, Ben M. "Georges Cuvier (1769–1832)". UCMP Berkeley. Retrieved 8 March 2018.
Cuvier's insistence on the functional integration of organisms led him to classify animals into four "branches," or embranchements: Vertebrata, Articulata (arthropods and segmented worms), Mollusca (which at the time meant all other soft, bilaterally symmetrical invertebrates), and Radiata (cnidarians and echinoderms).
- Cuvier, Georges; Griffith, Edward; Pidgeon, Edward (1834). The Mollusca and Radiata: Arranged by the Baron Cuvier, with Supplementary Additions to Each Order. Whittaker and Company. pp. 435–.
- Hadzi, J. (1963). The Evolution of the Metazoa. Macmillan. pp. 56–57. ISBN 978-0080100791.
- Chandra, Girish. "Symmetry". IAS. Retrieved 14 June 2014.
- Finnerty, J.R. (2003). "The origins of axial patterning in the metazoa: How old is bilateral symmetry?". The International Journal of Developmental Biology. 47 (7–8): 523–9. PMID 14756328. 14756328 16341006.
- Endress, P. K. (February 2001). "Evolution of Floral Symmetry". Current Opinion in Plant Biology. 4 (1): 86–91. doi:10.1016/S1369-5266(00)00140-0. PMID 11163173.
- Stewart, 2001. pp 64–65.
- Alan J Cann (2015). "Virus Structure". eLS. pp. 1–9. doi:10.1002/9780470015902.a0000439.pub2. ISBN 9780470015902.CS1 maint: uses authors parameter (link)
- Horne, R. W.; Wildy, P. (November 1961). "Symmetry in virus architecture". Virology. 15 (3): 348–373. doi:10.1016/0042-6822(61)90366-X. PMID 14448959.
- Holló, Gábor (2015). "A new paradigm for animal symmetry". Interface Focus. 5 (6): 20150032. doi:10.1098/rsfs.2015.0032. PMID 26640644.
- Young, K. D. (2006). "The Selective Value of Bacterial Shape". Microbiology and Molecular Biology Reviews. 70 (3): 660–703. doi:10.1128/MMBR.00001-06. PMC 1594593. PMID 16959965.
- Valentine, James W. "Bilateria". AccessScience. Archived from the original on 18 January 2008. Retrieved 29 May 2013.
- Finnerty, John R (2003). "Evolution & Development". IJDB. 47: 465–705.
- Holló, Gábor (2015). "A new paradigm for animal symmetry". Interface Focus. 5 (6): 20150032. doi:10.1098/rsfs.2015.0032. PMID 26640644.
- Freeman, Gary (2009). "The rise of bilaterians". Historical Biology. 21 (1–2): 99–114. doi:10.1080/08912960903295843. S2CID 83841216.
- Finnerty, John R. (2005). "Did internal transport, rather than directed locomotion, favor the evolution of bilateral symmetry in animals?". BioEssays. 27 (11): 1174–1180. doi:10.1002/bies.20299. PMID 16237677.
- "SCROPHULARIACEAE – Figwort or Snapdragon Family". Texas A&M University Bioinformatics Working Group. Retrieved 14 June 2014.
- Symmetry, biological, from The Columbia Electronic Encyclopedia (2007).
- Martindale, Mark Q.; Henry, Jonathan Q. (1998). "The Development of Radial and Biradial Symmetry: The Evolution of Bilaterality1" (PDF). American Zoology. 38 (4): 672–684. doi:10.1093/icb/38.4.672.
- Holló, Gábor (2015). "A new paradigm for animal symmetry". Interface Focus. 5 (6): 20150032. doi:10.1098/rsfs.2015.0032. PMID 26640644.
- Watanabe, Hiroshi; Schmidt, Heiko A.; Kuhn, Anne; Höger, Stefanie K.; Kocagöz, Yigit; Laumann-Lipp, Nico; Özbek, Suat; Holstein, Thomas W. (24 August 2014). "Nodal signalling determines biradial asymmetry in Hydra". Nature. 515 (7525): 112–115. Bibcode:2014Natur.515..112W. doi:10.1038/nature13666. PMID 25156256. S2CID 4467701.
- Cubas, Pilar; Vincent, Coral; Coen, Enrico (1999). "An epigenetic mutation responsible for natural variation in floral symmetry". Nature. 401 (6749): 157–161. Bibcode:1999Natur.401..157C. doi:10.1038/43657. PMID 10490023. S2CID 205033495.
- Citerne, H (2000). "Diversity of cycloidea-like Genes in Gesneriaceae in Relation to Floral Symmetry". Annals of Botany. 86: 167–176. doi:10.1006/anbo.2000.1178.
- Hileman, Lena C; Cubas, Pilar (2009). "An expanded evolutionary role for flower symmetry genes". Journal of Biology. 8 (10): 90. doi:10.1186/jbiol193. PMC 2790833. PMID 19895716.
- Grammer, K.; Thornhill, R. (1994). Human (Homo sapiens) facial attractiveness and sexual selection: the role of symmetry and averageness. Journal of comparative psychology (Washington, D.C. : 1983), 108(3), 233–42.
- Maynard Smith, John; Harper, David (2003). Animal Signals. Oxford University Press. pp. 63–65.
- Martindale, Mark Q.; Henry, Jonathon Q (1998). "The Development of Radial and Biradial Symmetry: The Evolution of Bilaterality". American Zoologist. 38 (4): 672–684. doi:10.1093/icb/38.4.672.
- Myers, Phil (2001). "Porifera Sponges". University of Michigan (Animal Diversity Web). Retrieved 14 June 2014.
- Norberg, R (1997). "Skull asymmetry, ear structure and function, and auditory localization in Tengmalm's owl, (Linné)". Philosophical Transactions of the Royal Society of London. B, Biological Sciences. 282: 325–410. doi:10.1098/rstb.1978.0014.
- Friedman, Matt (2008). "The evolutionary origin of flatfish asymmetry". Nature. 454 (7201): 209–212. Bibcode:2008Natur.454..209F. doi:10.1038/nature07108. PMID 18615083. S2CID 4311712.
- Lee, H. J.; Kusche, H.; Meyer, A. (2012). "Handed Foraging Behavior in Scale-Eating Cichlid Fish: Its Potential Role in Shaping Morphological Asymmetry". PLOS ONE. 7 (9): e44670. Bibcode:2012PLoSO...744670L. doi:10.1371/journal.pone.0044670. PMC 3435272. PMID 22970282.CS1 maint: multiple names: authors list (link)
- Zaidel, E. (2001). "Brain Asymmetry". International Encyclopedia of the Social & Behavioral Sciences. Elsevier. pp. 1321–1329. doi:10.1016/b0-08-043076-7/03548-8. ISBN 978-0-08-043076-8.
- Betts, J. Gordon (2013). Anatomy & physiology. pp. 787–846. ISBN 978-1-938168-13-0. Retrieved 11 August 2014.
- Holder, M. K. (1997). "Why are more people right-handed?". Scientific American. Retrieved 14 April 2008.
- Goss, Richard J. (1 June 1990). "Interactions between asymmetric brow tines in caribou and reindeer antlers". Canadian Journal of Zoology. 68 (6): 1115–1119. doi:10.1139/z90-165. ISSN 0008-4301.
- Hirokawa, Nobutaka; Tanaka, Yosuke; Okada, Yasushi; Takeda, Sen (2006). "Nodal Flow and the Generation of Left-Right Asymmetry". Cell. 125 (1): 33–45. doi:10.1016/j.cell.2006.03.002. PMID 16615888. S2CID 18007532.
- Nonaka, Shigenori; Shiratori, Hidetaka; Saijoh, Yukio; Hamada, Hiroshi (2002). "Determination of left–right patterning of the mouse embryo by artificial nodal flow". Nature. 418 (6893): 96–99. Bibcode:2002Natur.418...96N. doi:10.1038/nature00849. PMID 12097914. S2CID 4373455.
- Raya, Angel; Izpisua Belmonte, Juan Carlos (2004). "Unveiling the establishment of left–right asymmetry in the chick embryo". Mechanisms of Development. 121 (9): 1043–1054. doi:10.1016/j.mod.2004.05.005. PMID 15296970. S2CID 15417027.
- Gros, J.; Feistel, K.; Viebahn, C.; Blum, M.; Tabin, C. J. (2009). "Cell Movements at Hensen's Node Establish Left/Right Asymmetric Gene Expression in the Chick". Science. 324 (5929): 941–944. Bibcode:2009Sci...324..941G. doi:10.1126/science.1172478. PMC 2993078. PMID 19359542.
- Muñoz-Nortes, Tamara; Wilson-Sánchez, David; Candela, Héctor; Micol, José Luis (2014). "Symmetry, asymmetry, and the cell cycle in plants: known knowns and some known unknowns". Journal of Experimental Botany. 65 (10): 2645–2655. doi:10.1093/jxb/ert476. PMID 24474806.
Sources
- Ball, Philip (2009). Shapes. Oxford University Press.
- Stewart, Ian (2007). What Shape is a Snowflake? Magical Numbers in Nature. Weidenfeld and Nicolson.
- Thompson, D'Arcy (1942). On Growth and Form. Cambridge University Press.
- Haeckel, Ernst, E. (1904). Kunstformen der Natur. Available as Haeckel, E. (1998); Art forms in nature, Prestel USA. ISBN 3-7913-1990-6.

.jpg.webp)